- 2021-05-21 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
天津市静海区第一中学2019-2020学年高一下学期期中考试数学试题
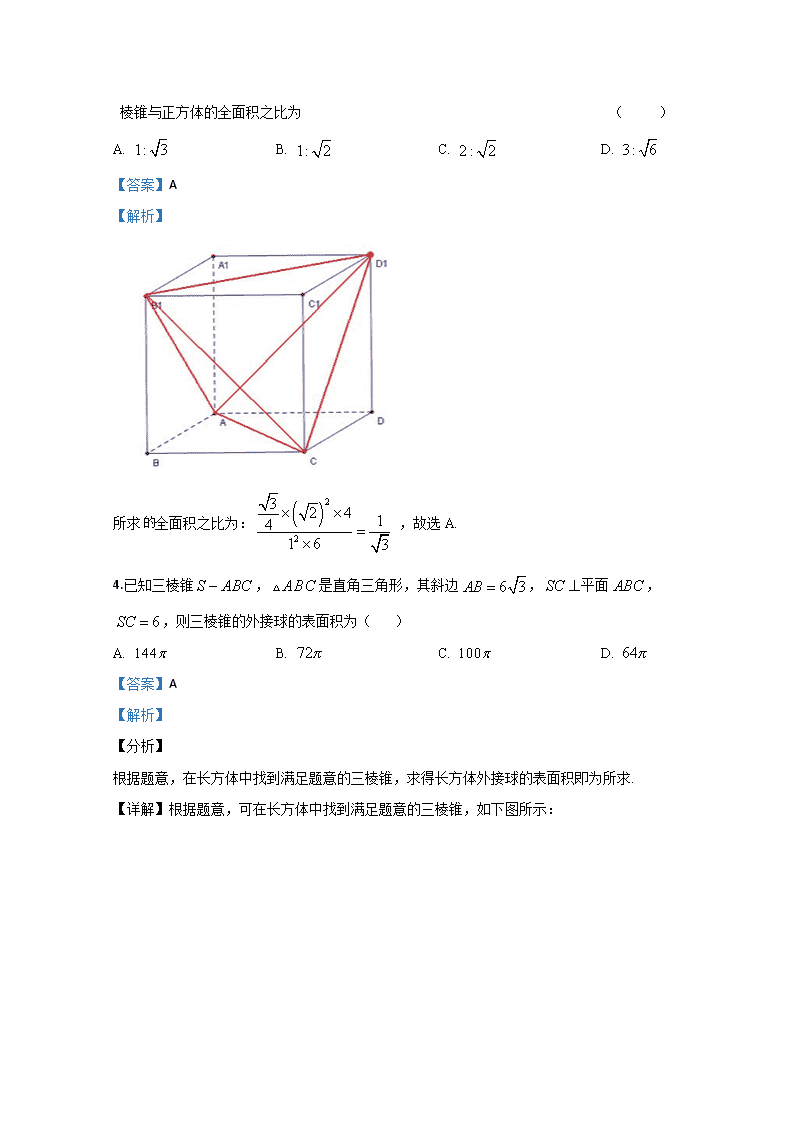
高一数学(期中) 一、选择题: 每小题4分,共28分. 1.复数对应的点落在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】C 【解析】 【分析】 利用复数的运算法则化简复数,根据复数的几何意义即可求得对应点,即可判断. 【详解】因为, 故其对应的点为, 容易知其位于第三象限. 故选:C. 【点睛】本题考查复数的运算以及复数的几何意义,属综合基础题. 2.在中,、、分别为角、、的对边,它的面积为,则角等于( ) A. B. C. D. 【答案】D 【解析】 【分析】 利用面积公式,借助余弦定理,即可容易求得结果. 【详解】因为,且, 故可得,即, 又因为,故可得. 故选:D. 【点睛】本题考查三角形的面积公式以及余弦定理的应用,属综合基础题. 3.已知正方体的个顶点中,有 个为一侧面是等边三角形的正三棱锥的顶点,则这个正三棱锥与正方体的全面积之比为 ( ) A. B. C. D. 【答案】A 【解析】 所求全面积之比为: ,故选A. 4.已知三棱锥,是直角三角形,其斜边,平面,,则三棱锥的外接球的表面积为( ) A. B. C. D. 【答案】A 【解析】 【分析】 根据题意,在长方体中找到满足题意的三棱锥,求得长方体外接球的表面积即为所求. 【详解】根据题意,可在长方体中找到满足题意的三棱锥,如下图所示: 故该长方体的外接球与三棱锥的外接球相同, 又长方体的长宽高可以为, 则外接球半径. 故其表面积. 故选:A. 【点睛】本题考查三棱锥外接球的求解,属基础题. 5.已知中,为边的两个三等分点,则( ) A. B. C. D. 【答案】B 【解析】 分析】 用基向量表示出目标向量,利用向量的数量积运算,即可求得结果. 【详解】根据题意,由平面向量的定比分点可得: , 故可得 . 故选:B. 【点睛】本题考查用基向量表示平面向量,以及向量的数量积运算,属综合基础题. 6.复数的虚部为( ) A. B. C. 3 D. -7 【答案】C 【解析】 【分析】 先求得,再利用复数运算法则,化简复数后,求其虚部即可. 【详解】因为, 故, 故其虚部为. 故选:C. 【点睛】本题考查复数的乘法运算,复数的模长求解,以及虚部的辨识,属综合基础题. 7.在锐角三角形ABC中,若,且满足关系式,则的取值范围是( ) A. B. C. D. 【答案】C 【解析】 【分析】 根据已知条件求得,构造的函数,通过求三角函数的值域,即可求得结果. 【详解】因为,故可得, 又,故可得. 因为,故可得 整理得,则. 故可得, 因为,故可得. 则 故可得. 故选:C. 【点睛】本题考查利用正余弦定理求解三角形中的范围问题,涉及正弦的和角公式,属综合困难题. 二、填空题:每小题5分,共25分. 8.已知向量,若与共线,则等于_______ 【答案】 【解析】 【分析】 根据已知条件,即可求的与的坐标,根据向量共线的坐标公式,即可求得结果. 【详解】因为, 故可得,, 因为与共线, 故可得,即可得. 故答案为:. 【点睛】本题考查向量坐标的运算,以及由向量共线求参数值,属基础题. 9.已知复数z满足(z-2)i=1+2i(i是虚数单位),则复数z的模为_____. 【答案】 【解析】 【分析】 根据复数的运算,即可求得复数,则模长得解. 【详解】因为(z-2)i=1+2i,故可得. 故可得. 故答案为:. 【点睛】本题考查复数的运算,以及复数模长的求解,属综合基础题. 10.在中,角所对的边分别为,若,,则=______ 【答案】 【解析】 【分析】 利用正弦定理将角化边,将用表示出来,用余弦定理,即可求得 【详解】因为,故可得; 因为,故可得; 综合即可求得. 由余弦定理可得. 又因为,故可得. 故答案为:. 【点睛】本题考查利用正弦定理将角化边,以及用余弦定理解三角形,属综合中档题. 11.已知某圆锥体的底面半径,沿圆锥体的母线把侧面展开后得到一个圆心角为的扇形,则该圆锥体的表面积是___ 【答案】 【解析】 【分析】 利用弧长公式,即可求得圆锥的母线,利用圆锥表面积公式即可求得结果. 【详解】因为底面圆周长,也即扇形的弧长为, 设圆锥母线长为,则可得,解得. 故可得圆锥的侧面积. 则表面积为 故答案:. 【点睛】本题考查扇形的弧长公式,以及圆锥侧面积的求解,属综合基础题. 12.如图,已知等腰梯形中,是的中点,是线段上的动点,则的最小值是_____ 【答案】 【解析】 【分析】 以中点为坐标原点,建立平面直角坐标系,用解析法将目标式转化为函数,求得函数的值域,即可求得结果. 【详解】以中点为坐标原点,建立平面直角坐标系,如下图所示: 由题可知,, 设,,故可得, 则, 故可得, 因的对称轴, 故可得的最小值为. 故答案为:. 【点睛】本题考查用解析法求向量数量积的最值,涉及动点问题的处理,属综合中档题. 三、解答题(52分) 13.如图所示,在长方体中,, 为棱上—点. (1) 若,求异面直线和所成角的大小; (2) 若,求证平面. 【答案】(1) ;(2)证明详见解析. 【解析】 【分析】 (1) 由,得是异面直线和所成角,由此能示出异面直线和所成角的正切值; (2) 时,由勾股定理逆定理得,,由此能证明平面 . 【详解】(1), 是异面直线和所成角, ∵在长方体中,平面, , ,,,M为棱上一点,, , , 即异面直线和所成角的大小为. (2) 时,, ,. ,, , , 又,平面. 【点睛】本题考查异面直线所成角的正切值的求法,考查直线与平面的证明,解题时要注意空间思维能力的培养. 14.已知,的夹角为45°. (1)求方向上的投影; (2)求的值; (3)若向量夹角是锐角,求实数的取值范围. 【答案】(1)1;(2);(3). 【解析】 试题分析:(1)由射影定义可得在方向上的投影;(2)利用公式可求得向量的模;(3)由与的夹角是锐角,可得,且与不能同向共线,即可解出实数的取值范围. 试题解析:(1)∵,,与的夹角为 ∴ ∴在方向上的投影为1 (2)∵ ∴ (3)∵与的夹角是锐角 ∴,且与不能同向共线 ∴,, ∴或 15.在中,角、、所对的边分别为、、. (1)若,,求面积的最大值; (2)若,试判断的形状. (3)结合解答第(2)问请你总结一下在解三角形中判断三角形的形状的方法. 【答案】(1);(2)直角三角形或等腰三角形. (3)见解析 【解析】 【分析】 (1)利用余弦定理列出关系式,将,代入,整理后利用基本不等式求出的最大值,即可确定出三角形面积的最大值; (2)根据三角形内角和定理,得到,代入已知等式,展开化简合并,得 ,最后讨论当时与时,分别对的形状加以判断,可以得到结论. (3)根据(2)中所求,结合解三角形的知识,即可容易总结. 【详解】(1)因为,, 所以由余弦定理得:,即, 整理得,因为,所以, 即,所以, 当且仅当时取等号, 则的最大值为. (2)由,所以, 化简得,即, 所以或, 因为与都为三角形内角, 所以或, 所以是直角三角形或等腰三角形. (3)根据(2)中所求,结合已知知识,总结如下: 一、可利用正余弦定理,求得三角形中的角度,即可判断三角形形状; 二、可利用正余弦定理,求得三角形中的边长,由余弦定理判断三角形形状. 【点睛】本题考查利用正余弦定理求解三角形面积的最值,以及判断三角形的形状,属综合中档题. 16.如图,四边形为矩形,且平面, ,为的中点. (1)求证:; (2)求三棱锥的体积; (3)探究在上是否存在点,使得平面,并说明理由. 【答案】(1)见解析;(2);(3)见解析. 【解析】 【分析】 (1)连结,由几何体的空间结构可证得,利用线面垂直的定义可知. (2)由(1)知为腰长为1的等腰直角三角形,结合题意转化顶点可得. (3)在上存在中点,使得.取的中点,连结. 易证得四边形EGHC是平行四边形,所以EG//CH,结合线面平行的判断定理可知EG//平面PCD. 【详解】(1)连结,∵为的中点,, ∴为等腰直角三角形, 则,同理可得,∴,∴, 又,且, ∴, 又∵,∴,又,∴. (2)由(1)知为腰长为1的等腰直角三角形, ∴,而是三棱锥的高, ∴. (3)在上存在中点,使得.理由如下: 取的中点,连结. ∵是的中点, ∴,且, 又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=AD, 所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH, 又EG平面PCD,CH平面PCD,所以EG//平面PCD. 【点睛】本题主要考查线面垂直的判断定理,线面垂直的判断定理,棱锥的体积公式,立体几何中探索问题的处理方法等知识,意在考查学生的转化能力和计算求解能力. 17.在△ABC中角A、B、C的对边分别为设向量,且, (1)若=,求A; (2)若的外接圆半径为1,且试确定的取值范围. 【答案】(1)或;(2) 【解析】 【分析】 由已知条件,即可求得; (1)利用两角的关系,结合辅助角公式即可求得; (2)将目标式转化为的混合式,令,利用其与之间的关系,求得函数的值域,即可求得结果. 【详解】因为且, 所以,由正弦定理,得, 即. 又,故,因为, 所以即. (1)= , 得,. (2)若则,由正弦定理,得 设=,则, 所以 即, 所以实数的取值范围为. 【点睛】本题考查利用正余弦定理解三角形,涉及之间的关系以及换元法,属综合中档题.查看更多