高一数学必修5课件-3简单的线性规划问题

高一数学必修5课件-3简单的线性规划问题

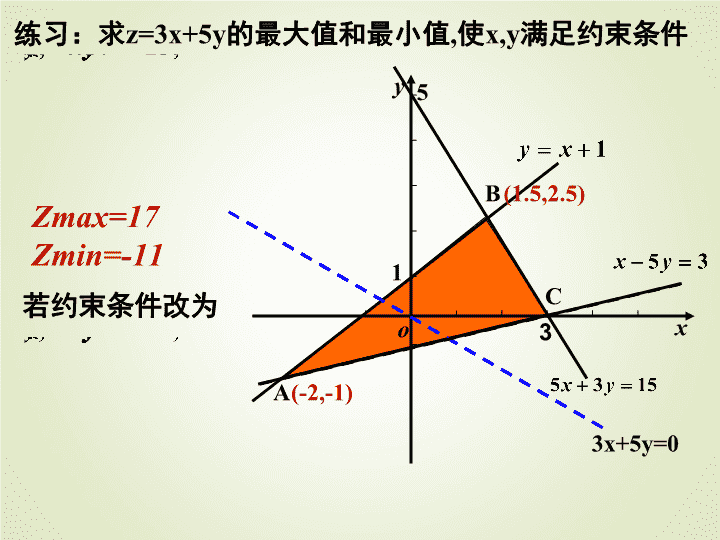
解线性规划问题的步骤： （3）移：作l0，利用平移的方法找出与可行域有公共 点且纵截距最大或最小的直线； （4）求：通过解方程组求出最优解； （5）答：作出答案。 （2）画：画可行域； （1）列：设出未知数,列出约束条件和目标函数； 一、复习回顾 5 3 15, 1, 5 3. x y y x x y         3 5 1 A B x y o 1535  yx 1 xy 35  yx (1.5,2.5) (-2,-1) Zmax=17 Zmin=-11 练习：求z=3x+5y的最大值和最小值,使x,y满足约束条件 C 3x+5y=0 若约束条件改为 5 3 15, 1, 5 3. x y y x x y         例1、某公司计划2011年在甲、乙两个电视台做总时间不超过300 分钟的广告，广告总费用不超过9万元。甲、乙电视台的广告收 费标准分别为500元/分钟和200元/分钟。假定甲、乙两个电视台 为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万 元和0.2万元，问该公司如何分配在甲、乙两个电视台的广告时 间，才能使公司的收益最大，最大收益是多少万元？ 解：设公司在甲电视台和乙电视台做广告的时间分别 为x分钟和y分钟，总收益为z元，由题意得 300 500 200 90000, 0, 0 x y x y x y         目标函数为z=3000x+2000y. 二、例题分析 300 5 2 900 0, 0 x y x y x y         即 作出二元一次不等式组所表示的平面 区域，即可行域，如图. 由图知，当直线l过M点时，目标函数取得最大值 300 ,5 2 900 x y x y      联立 ∴点M (100，200), 答：该公司在甲电视台做100分钟广告，在乙电视台做 200分钟广告。公司的收益最大，最大值为70万元. 解得x=100，y=200， ∴zmax=3000x+2000y=700000(元) 将z=3000x+2000y化为 .3 1 2 2000y x z   3 1 2 2000 z这是一组斜率为 ，纵截距为 的平行直线 例2、某工厂生产甲、乙两种产品。已知生产甲种产品1t需消耗 A种矿石10t、B种矿石5t、煤4t；生产乙种产品1t需消耗A种矿 石4t、B种矿石4t、煤9t。每1t甲种产品的利润是600元，每1t乙 种产品的利润是1000元。工厂在生产这两种产品的计划中要求 消耗A种矿石不超过300t、消耗B种矿石不超过200t、消耗煤不 超过360t。甲、乙两种产品应各生产多少(精确到0.1t)，能使利 润总额达到最大? 甲产品 （1t） 乙产品 （1t） 资源限额 （t） A种矿石（t） B种矿石（t） 煤（t） 利润（元） 产品消耗量 资源 列表： 5 10 4 600 4 4 9 1000 300 200 360 解：设生产甲、乙两种产品，分别为 x t、yt，利润总额为z元 把题中限制条件进行转化： 约束条件 10x+4y≤300 5x+4y≤200 4x+9y≤360 x≥0 y ≥0 z=600x+1000y. 目标函数： 甲产品 （1t） 乙产品 （1t） 资源限额 （t） A种矿石（t） B种矿石（t） 煤（t） 利润（元） xt yt 产品消耗量 资源 5 10 4 600 4 4 9 1000 300 200 360 0 x y 10 20 10 解：设生产甲、乙产品分别为xt、yt，则 作出以上不等式组所表示的可行域 作出一组平行直线 600x+1000y=t 解得交点M的坐标为(12.4，34.4) 10x+4y=300 5x+4y=200 4x+9y=360 600x+1000y=0 M 答:应生产甲产品约12.4吨，乙产 品34.4吨，能使利润总额达到最 大。 (12.4,34.4) 经过可行域上的点M时，目 标函数在y轴上截距最大 9030 75 40 50 40此时z=600x+1000y取得最大值. 利润总额为 z=600x+1000y 元 10x+4y≤300 5x+4y≤200 4x+9y≤360 x≥0 y ≥0 5 4 200 4 9 360 x y x y      由 例3、要将两种大小不同规格的钢板截成A、B、C三种规格，每 张钢板可同时截得三种规格的小钢板的块数如下表所示 ： 解：设需截第一种钢板 x 张，第一种钢板 y 张，则 规格类型 钢板类型 第一种钢板 第二种钢板 A规格 B规格 C规格 2 1 2 1 3 1 作出可行域（如图） 目标函数为 z=x+y 今需要A,B,C三种规格的成品分别为15，18，27块，问各截这两 种钢板多少张可得所需三种规格成品，且使所用钢板张数最少。 X张 y张 2x+y≥15, x+2y≥18, x+3y≥27, x≥0,x∈N y≥0,x∈N 2x+y=15 x+2y=18 x+3y=27 x y O 4 8 12 16 20 4 8 12 16 20 24 28 30 B(3,9) C(4,8)A(18/5,39/5) x+y =0 直线x+y=12经过的整点是B(3,9)和C(4,8)，它们是最优解. 目标函数为z= x+y 化为y=-x+z 当直线经过点A时 z=x+y=11.4 解得交点B,C的坐标B(3,9)和C(4,8) 调整优值法 但它不是最优整数解， 作直线 x+y=12 答（略） x+y=12 作出可行域（如图） 这是斜率为-1，纵 截距为z的一组平 行直线， 经过可行域内的整点B(3,9)和C(4,8)时，t=x+y=12是最优解. 答:(略) 打网格线法 在可行域内打出网格线， 将直线x+y=11.4继续向上平移， 2x+y≥15, x+2y≥18, x+3y≥27, x≥0,x∈N y≥0,x∈N 作出一组平行直线 目标函数为 z= x+y 当直线经过点A时 z=x+y=11.4 但它不是最优整数解， 2x+y=15 x+2y=18 x+3y=27 x y O 4 8 12 16 20 4 8 12 16 20 24 28 30 B(3,9) C(4,8)A(18/5,39/5) x+y =0 x+y=12 在可行域内找出最优解、线性规划整 数解问题的一般方法是： 1、若区域“顶点”处恰好为整点，那么它就是最优 解；（在包括边界的情况下） 2、若区域“顶点”不是整点或不包括边界时，应先 求出该点坐标，并计算目标函数值Z，然后在可行域 内适当放缩目标函数值，使它为整数，且与Z最接近， 在这条对应的直线中，取可行域内整点，如果没有整 点，继续放缩，直至取到整点为止。 3、在可行域内找整数解，一般采用平移找解法，即 打网络、找整点、平移直线、找出整数最优解 练习.某工厂用A、B两种配件生产甲、乙两种产品，每生产 一件甲产品使用 4 个A配件耗时 1h，每生产一件乙产品使 用4个B配件耗时2h，该厂每天最多可从配件厂获得16个A 配件和12个B配件，按每天工作8 h计算，该厂所有可能的 日生产安排是什么？ 解：设甲、乙两种产品 分别生产x、y件，则有 2 8 0 4 0 3 x y x y         (x，y∈Z) 2 8 4 1 6 4 1 2 0 0 x y x y x y        ＋ A配件 B配件 耗时 甲产品 乙产品 总数 4 0 1 0 4 2 16 12 8 2 8 0 4 0 3 x y x y         (x，y∈Z) x y O 4 8 4 2 2 6 x=4 y=3 x+2y=8 右图阴影部分中的整点 (坐标为整数)就代表所 有可能的日生产安排。 练习.某工厂用A、B两种配件生产甲、乙两种产品，每生产 一件甲产品使用 4 个A配件耗时 1h，每生产一件乙产品使 用4个B配件耗时2h，该厂每天最多可从配件厂获得16个A 配件和12个B配件，按每天工作8 h计算，该厂所有可能的 日生产安排是什么？ 4 3 12 1 0 ( ) 2 4 5 8 x y x y y A B C D         不等式组 表示的平面区域内 的整点的个数是 、个 、个 、 随 个 ： 、 练 个 C x y O 4 3-1 x-y+1=0 4x+3y-12=0 课本P91阅读与思考： 已知 ，求4x+2y的取值范围。1≤x+y≤3 -1≤x-y≤1 x y 1 2 3O 1 2 3 x+y=1 x+y=3x-y=1 x-y=-1 (2,1)(0,1) 解线性规划应用问题的一般步骤： 2）设好变元并列出不等式组和目标函数 3）由二元一次不等式表示的平面区域做出可行域； 4）在可行域内求目标函数的最优解 1）理清题意，列出表格 5)还原成实际问题 (准确作图，准确计算)