- 2021-05-21 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北京平谷区2014年中考数学一模试题目
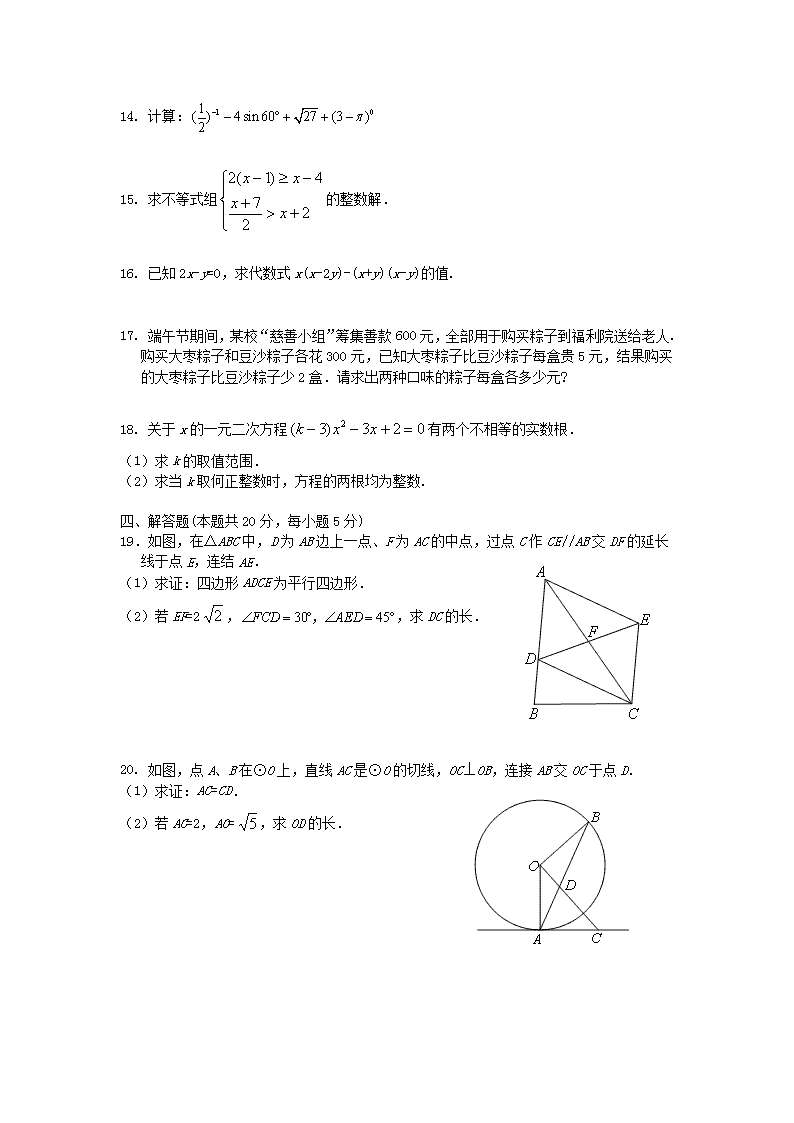
北京市平谷区2014年中考一模数学试题 考 生 须 知 1.本试卷共6页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上认真填写学校、班级、姓名和考号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,请将本试卷、答题卡一并交回. 一、选择题(本题共32分,每小题4分) 1.西部大开发战略是党中央面向21世纪的重大决策,我国西部地区面积为6 400 000平方千米,将6 400 000用科学记数法表示应为 A. B. C. D. 2. 的相反数是( ) A. B. C. D. 3. 在一个口袋中,装有质地、大小均相同、颜色不同的红球3个,蓝球4个,黄球5个,现在随机抽取一个球是红球的概率是 A. B. C. D. 4.如图,AB∥CD,AF交CD于点O,且OF平分∠EOD, 如果∠A=34°,那么∠EOD的度数是 A.34° B.68° C.102° D.146° 图2 900cm 图1 60cm 80cm 5.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对 校园中一些物体进行了测量.下面是他们通过测量得到的一些信息: 如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm. 如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为 A.900cm B.1000cm C.1100cm D.1200cm 6.某校篮球班21名同学的身高如下表: 身高(cm) 180 186 188 192 208 人数(个) 4 6 5 4 2 则该校篮球班21名同学身高的众数和中位数分别是 A.186,188 B.188,186 C.186,186 D.208,188 7. 下列图形中,既是轴对称图形又是中心对称图形的是( ) A B C D 8.如图,在矩形ABCD中,AB=9,BC=3,点E是沿A→B方向运动,点F是沿A→D→C方向运动.现E、F两点同时出发匀速运动,设点E的运动速度为每秒1个单位长度,点F的运动速度为每秒3个单位长度,当点F运动到C点时,点E立即停止运动.连接EF,设点E的运动时间为x秒,EF的长度为y个单位长度,则下列图象中,能表示y与x的函数关系的图象大致是 x 1 4 y O x 1 4 y O x 1 4 y O x 1 4 y O A B C D 二、填空题(本题共16分,每小题4分) 9. 分解因式:= . 10.请写出一个开口向下,对称轴为直线的抛物线的解析式,y= . 11.如图,点O是矩形ABCD的对称中心,E是AB上的点, 沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE 的长为_____________________. 12.如图,、、…(n为正整数)分别是反比例函数在第一象限图像上的点,、、…分别为x轴上的点,且、、…均为等边三角形.若点的坐标为(2,0),则点的坐标为____________,点的坐标为____________. 三、解答题(本题共30分,每小题5分) 13. 如图,点A、C、D、B 四点共线,且AC=DB,∠A=∠B,∠E=∠F. 求证:DE=CF. 14. 计算: 15. 求不等式组的整数解. 16. 已知2x-y=0,求代数式x(x-2y)-(x+y)(x-y)的值. 17. 端午节期间,某校“慈善小组”筹集善款600元,全部用于购买粽子到福利院送给老人.购买大枣粽子和豆沙粽子各花300元,已知大枣粽子比豆沙粽子每盒贵5元,结果购买的大枣粽子比豆沙粽子少2盒.请求出两种口味的粽子每盒各多少元? 18. 关于x的一元二次方程有两个不相等的实数根. (1)求k的取值范围. (2)求当k取何正整数时,方程的两根均为整数. 四、解答题(本题共20分,每小题5分) 19.如图,在△ABC中,D为AB边上一点、F为AC的中点,过点C作CE//AB交DF的延长线于点E,连结AE. (1)求证:四边形ADCE为平行四边形. (2)若EF=2,,求DC的长. 20. 如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D. (1)求证:AC=CD. (2)若AC=2,AO=,求OD的长. 21.由平谷统计局2013年12月发布的数据可知,我区的旅游业蓬勃发展,以下是根据近几年我区旅游业相关数据绘制统计图的一部分: 北京市平谷区2012年旅游 营业收入统计图 北京市平谷区2008-2013年旅游 营业收入统计图 请你根据以上信息解答下列问题: (1)计算2012年平谷区旅游区点营业收入占全区旅游营业收入的百分比,并补全扇形统计图; (2)2012年旅游区点的收入为2.1万元,请你计算2012年平谷区旅游营业收入,并补全条形统计图 (结果保留一位小数) ; (3)如果今年我区的旅游营业收入继续保持2013年的增长趋势,请你预测我区今年的旅游营业收入 (结果保留一位小数) . 22.如图1,在△ABC中,E、D分别为AB、AC上的点,且ED//BC,O为DC中点,连结EO并延长交BC的延长线于点F,则有S四边形EBCD=S△EBF. (1)如图2,在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.将直线MN绕着点P旋转的过程中发现,当直线MN满足某个条件时,△MON的面积存在最小值.直接写出这个条件:_______________________. (2)如图3,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、(,)、(4、2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值. 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.如图,在平面直角坐标系中,直线与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D. (1)求抛物线的解析式; (2)设点P的横坐标为m. ①用含m的代数式表示线段PD的长,并求出线段PD长的最大值; ②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为1:2.若存在,直接写出m的值;若不存在,请说明理由. 24.(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF, 则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足,请证明这个等量关系; (2)在△ABC中, AB=AC,点D、E分别为BC边上的两点. ①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________; ②如图3,当∠BAC=,(0°<<90°),∠DAE=时,BD、DE、EC应满足的等量关系是____________________.【参考:】 25.在平面直角坐标系中,已知抛物线y=-x2+bx+c (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限. (1)如图,若该抛物线过A,B两点,求b,c的值; (2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与直线AC交于另一点Q. ①点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M,P,Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时,求点M的坐标; ②取BC的中点N,连接NP,BQ.当取最大值时,点Q的坐标为________. 平谷区2013-2014学年度第二学期初三统练参考答案 初三数学 一、选择题(本题共32分,每小题4分) 1.B ; 2.A; 3.C; 4.B; 5.D; 6.A; 7.D; 8.C. 二、填空题(本题共16分,每小题4分) 9.; 10. 答案不唯一,比如:; 11.; 12.. 三、解答题(本题共30分,每小题5分) 13. (本小题满分5分) 证明:∵AC=DB, ∴AC+CD=DB+CD,即AD=BC-----------------------------------------------------------------------1分 在△AED和△BFC中 ∴△AED≌△BFC. --------------------------------------------------------------------------------------4分 ∴DE=CF. -------------------------------------------------------------------------------------------------5分 14.(本小题满分5分) ----------------------------------------------------------------------------5分 ----------------------------------------------------------------4分 15.(本小题满分5分) 解不等式①,得 ----------------------------------------------------------------------------1分 解不等式②,得 -----------------------------------------------------------------------------2分 ∴不等式组的解集为 --------------------------------------------------------------4分 ∴不等式组的整数解为-2、-1、0、1、2. ----------------------------------------------------5分 16.(本小题满分5分) 解: x(x-2y)-(x+y)(x-y) =x2-2xy-(x2-y2) --------------------------------------------------------------------------------------------2分 = x2-2xy-x2+y2 =-2xy +y2 -----------------------------------------------------------------------------------------------3分 ∵2x-y=0, ∴原式=-y(2x-y) -------------------------------------------------------------------------------------------4分 =0 -------------------------------------------------------------------------------------------------5分 17.(本小题满分5分) 解:设豆沙粽子每盒x元,则大枣粽子每盒(x+5)元.-------------------------------------------1分 依题意得 ------------------------------------------------------------------------2分 解得 -----------------------------------------------------------------------------3分 经检验是原方程的解,但不符合题意,舍去 当时, ---------------------------------------------------------------------------4分 答:大枣粽子每盒30元,豆沙粽子每盒25元.--------------------------------------------------5分 18.(本小题满分5分) 解:(1)方程有两个不相等的实数根,∴ ---------------------1分 解得,. ------------------------------------------------------------------------2分 (2)k的正整数值为 1、2、4. -----------------------------------------------------------3分 如果k=1,原方程为. 解得,,不符合题意 舍去. 如果k=2,原方程为, 解得,不符合题意,舍去. 如果k=4,原方程为,解得,符合题意. ----------------4分 ∴ k=4. --------------------------------------------------------------------------------------------5分 19.(本小题满分5分) (1)证明:∵CE//AB,∴∠DAF=∠ECF. ∵F为AC的中点,∴AF=CF. 在△DAF和△ECF中 ∴ △DAF≌△ECF. ∴ AD=CE. ------------------------------------------------------------------------------------2分 ∵CE//AB, ∴ 四边形ADCE为平行四边形. --------------------------------------------------------------------3分(2)作FH⊥DC于点H. ∵ 四边形ADCE为平行四边形. ∴ AE//DC,DF= EF=2, ∴∠FDC =∠AED=45°. 在Rt△DFH中,∠DHF=90°,DF=2,∠FDC=45°, ∴ sin∠FDC=,得FH=2, tan∠FDC=,得DH=2. ----------------------------------------------------------------------4分 在Rt△CFH中,∠FHC=90°,FH=2,∠FCD=30°,∴ FC=4. 由勾股定理,得HC=. ∴ DC=DH+HC=2+. ------------------------------------------------------------------------5分 20. (本小题满分5分) 解:(1)∵OA=OB,∴∠OAB=∠B. --------------------------------------------------------------1分 ∵直线AC为⊙O的切线, ∴∠OAC=∠OAB+∠DAC=90°. ----------------------------------------------------------------------2分 ∵OB⊥OC,∴∠BOC=90°. ∴∠ODB+∠B=90°.∴∠DAC=∠ODB. ∵∠ODB=∠CDA,∴∠DAC=∠CDA,∴AC=CD. -----------------------------------------------------------------------3分 (2)在Rt△OAC中,AC=CD=2,AO=,OC=OD+DC=OD+2,--------------------------4分 根据勾股定理得:OC2=AC2+AO2,即, 解得:OD=1.----------------------------------------------------------------------------------------------5分 21. (本小题满分5分) (1) 8.6% 和补充扇形统计图(图略) ------------------------------------------------------------2分 (2) 约24.4万元和补充条形统计图(图略) ----------------------------------------------------4分 (3) ,(万元) 我区今年的旅游营业收入约29.4万元. ------------------------------------------------------5分 22. (本小题满分5分) 解:(1)当直线MN旋转到点P是线段MN的中点时, △MON的面积最小.------------1分 (2)分两种情况: ①如图3①过点P的直线l 与四边形OABC 的一组对边 OC、AB分别交于点M、N. 延长OC、AB交于点D,易知AD = 6,S△OAD=18 . 由(1)的结论知,当PM=PN时,△MND的面积最小,此时四边形OANM的面积最大. 过点P、M分别作PP1⊥OA,MM1⊥OA,垂足分别为P1、M1. 由题意得M1P1=P1A = 2,从而OM1=MM1= 2. 又P(4,2),B(6,3) ∴P1A=M1P1=O M1=P1P=2,M1 M=OM=2,可证四边形MM1P1P是正方形. ∴MN∥OA,∠MND=90°,NM=4,DN=4.求得S△MND=8 ----------------------------------2分 ∴ ------------------------------------------------3分 图3① 图3 ② ② 如图3②,过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N. 延长CB交x轴于T点,由B、C的坐标可得直线BC对应的函数关系式为 y =-x+9 . 则T点的坐标为(9,0). ∴S△OCT= ×9×=. -----------------------------------------------------------------------------4分 由(1)的结论知:当PM=PN时,△MNT的面积最小,此时四边形OCMN的面积最大. 过点P、M点分别作PP1⊥OA,MM1⊥OA,垂足为P1 ,M1. 从而 NP1 =P1M1,MM1=2PP1=4. ∴点M的横坐标为5,点P(4、2),P1M1= NP1 = 1,TN =6. ∴S△MNT= ×6×4=12,S四边形OCMN=S△OCT-S△MNT = -12=<10. 综上所述:截得四边形面积的最大值为10. -----------------------------------------------------5分 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.(1)在中,当y=0时,x=-1;当y=5时,x=4. A(-1,0)、B(4,5) ------------------ ------------------------------------------------------1分 将A(-1,0)、B(4,5)分别代入y=ax2+bx-3中,得 解得,. ∴所求解析式为y=x2-2x-3 ---------------------------------------------------------------------2分 (2)①设直线AB交y轴于点E,求得E(0,1),∴OA=OE,∠AEO=45°, ∠ACP=∠AEO=45°, ∴. ---------------------------------------3分 设,则, ∴. --------------------------------------------4分 ∴. ∴PD的最大值为. ----------------------------------------------------------------------5分 ②当m=0或m=3时,PC把△PDB分成两个三角形的面积比为1:2. -------------7分 24. (1) 在正方形ABCD中,AB=AD,∠BAD=90°, ∠ABM=∠ADN=45°. 把△ABM绕点A逆时针旋转90°得到. 连结.则, ,. ∵∠EAF=45°,∴∠BAM+∠DAN=45°, ∠DAM′+∠DAF=45°, . ∴≌. ∴=MN. 在中,, ∴ -------------------------------------------------------------------3分 (2)① ; ------------------------------------------------------5分 ② ----------------------------------------------7分 25.解:(1)由题意,得点B的坐标为(4,–1). --------------------------------------------------1分∵抛物线过点A(0,–1),B(4,–1)两点, ∴解得 ---------------------------------------------------------3分 (2)由(1)得 . ①∵A的坐标为(0,–1),C的坐标为(4,3). ∴直线AC的解析式为:y=x-1. 设平移前的抛物线的顶点为P0,可得(2,1),且在直线AC上. ∴. -----------------------------------------------------------4分 ∵点P在直线AC上滑动,且与直线AC交于另一点Q. ∴PQ =AP0=2. ---------------------------------------------------------------------------------------5分 ∵PQ为直角边,M到PQ的距离为2(即为PQ的长). 由A(0,-1),B(4,-1),P0(2,1)可知: △ABP0为等腰直角三角形,且BP0⊥AC,BP0=2. 过点B作直线l1∥AC,直线l1与抛物线y=-x2+2x-1的交点即为符合条件的点M. ∴可设直线l1的解析式为:y=x+b1. 又∵点B的坐标为(4,–1),∴-1=4+b1.解得b1=-5. ∴直线l1的解析式为:y=x-5. 解方程组得: ∴M1(4,-1),M2(-2,-7). -----------------------------------------------------------------6分 ② 点Q的坐标为--------------------------------------------------------------------------------8分 以上答案仅供参考,不同做法酌情给分!查看更多