- 2021-05-20 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中文科数学高考模拟试卷含答案
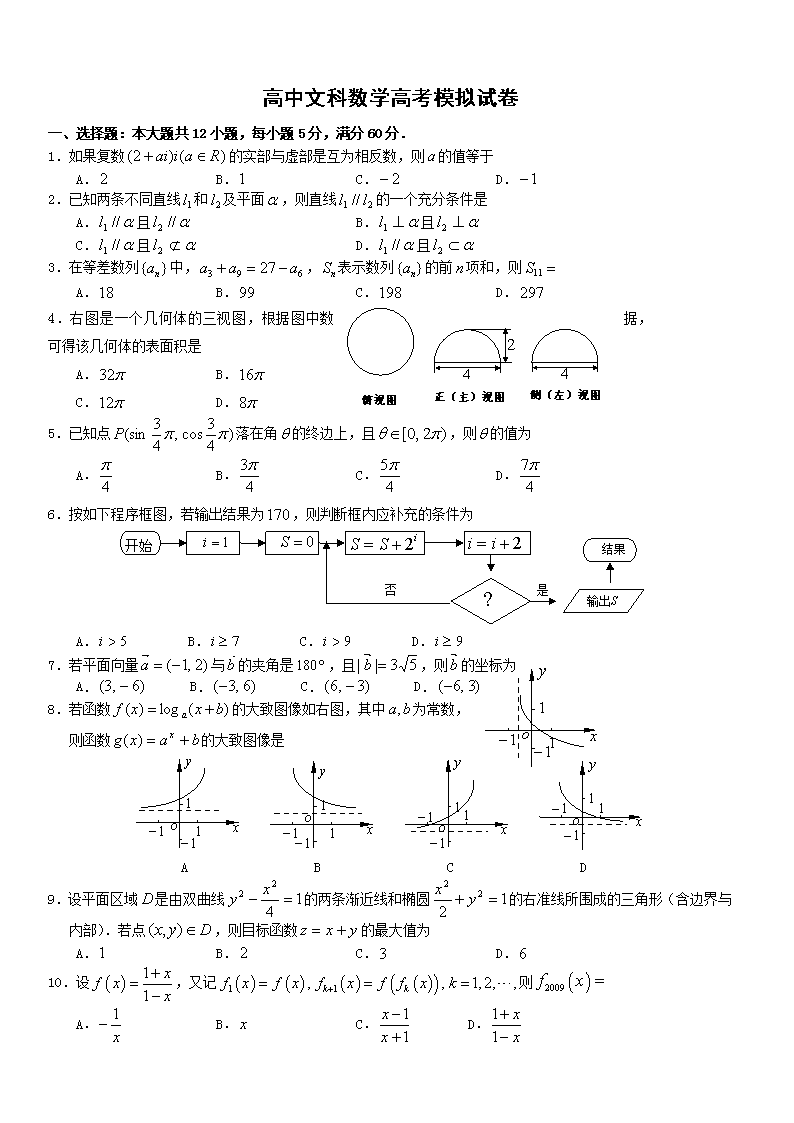
1 1 1 1 y o x 高中文科数学高考模拟试卷 一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分. 1.如果复数 )()2( Raiai 的实部与虚部是互为相反数,则 a 的值等于 A. 2 B.1 C. 2 D. 1 2.已知两条不同直线 1l 和 2l 及平面 ,则直线 21 // ll 的一个充分条件是 A. //1l 且 //2l B. 1l 且 2l C. //1l 且 2l D. //1l 且 2l 3.在等差数列 }{ na 中, 693 27 aaa , nS 表示数列 }{ na 的前 n 项和,则 11S A.18 B.99 C.198 D. 297 4.右图是一个几何体的三视图,根据图中数据, 可得该几何体的表面积是 A. 32 B. 16 C. 12 D. 8 5.已知点 )4 3cos,4 3(sin P 落在角 的终边上,且 )2,0[ ,则 的值为 A. 4 B. 4 3 C. 4 5 D. 4 7 6.按如下程序框图,若输出结果为170 ,则判断框内应补充的条件为 开始 1i 0S iSS 2 2 ii ?否 S输出 结果 是 A. 5i B. 7i C. 9i D. 9i 7.若平面向量 )2,1(a 与b 的夹角是 180 ,且 53|| b ,则 b 的坐标为 A. )6,3( B. )6,3( C. )3,6( D. )3,6( 8.若函数 )(log)( bxxf a 的大致图像如右图,其中 ba, 为常数, 则函数 baxg x )( 的大致图像是 1 1 1 1 y o x 1 11 1 y o x 1 1 1 1 y o x 1 11 1 y o x A B C D 9.设平面区域 D 是由双曲线 14 2 2 xy 的两条渐近线和椭圆 12 2 2 yx 的右准线所围成的三角形(含边界与 内部).若点 Dyx ),( ,则目标函数 yxz 的最大值为 A.1 B. 2 C.3 D. 6 10.设 1 1 xf x x ,又记 1 1, , 1,2, ,k kf x f x f x f f x k 则 2009 f x A. 1 x B. x C. 1 1 x x D.1 1 x x 2 4 侧(左)视图正(主)视图俯视图 4 11. 等差数列 na 中, 8776 , SSSS ,真命题有__________(写出所有满足条件的序号) ①前七项递增,后面的项递减 ② 69 SS ③ 1a 是最大项 ④ 7S 是 nS 的最大项 A.②④ B.①②④ C.②③④ D.①②③④ 12. 已知 ( )f x 是定义在 R 上的且以 2 为周期的偶函数,当 0 1x 时, 2( )f x x ,如果直线 y x a 与曲线 ( )y f x 恰有两个交点,则实数 a 的值为 A.0 B. 2 ( )k k Z C. 12 2 ( )4k k k Z 或 D. 12 2 ( )4k k k Z 或 二、填空题:本大题共 4 小题,每小题 4 分,满分 16 分。 13.某大型超市销售的乳类商品有四种:纯奶、酸奶、婴幼儿奶粉、成人奶粉,且纯奶、酸奶、婴幼儿奶粉、成 人奶粉分别有30 种、10 种、35 种、 25 种不同的品牌.现采用分层抽样的方法从中抽取一个容量为 n 的样 本进行三聚氰胺安全检测,若抽取的婴幼儿奶粉的品牌数是 7 ,则 n 。 14.若关于 x 的不等式 2 | | 2 0ax x a 的解集为 ,则实数 a 的取值范围为 。 15.在 ABCRt 中,若 aBCbACC ,,900 ,则 ABC 外接圆半径 2 22 bar 。 运 用 类 比 方 法 , 若 三 棱 锥 的 三 条 侧 棱 两 两 互 相 垂 直 且 长 度 分 别 为 cba ,, , 则 其 外 接 球 的 半 径 R = 。 16. 在 OAB 中,O 为坐标原点, ( 1,cos ), (sin ,1), 0, 2A B 。 ⑴若 ,OA OB OA OB 则 ,⑵ OAB 的面积最大值为 。 三、解答题:本大题 6 小题,满分 74 分。 17.(本小题满分 12 分)已知函数 2( ) 2cos cos( ) 3sin sin cos6f x x x x x x . (Ⅰ)求 ( )f x 的最小正周期;(Ⅱ)设 ]2,3[ x ,求 ( )f x 的值域. 18.(本小题满分 10 分)先后随机投掷 2 枚正方体骰子,其中 x 表示第1枚骰子出现的点数, y 表示第 2 枚骰子 出现的点数. (Ⅰ)求点 ),( yxP 在直线 1 xy 上的概率; (Ⅱ)求点 ),( yxP 满足 xy 42 的概率. FA E C O BD M 19.(本小题满分 13 分) 如图, AB 为圆O 的直径,点 E 、 F 在圆 O 上, EFAB // ,矩形 ABCD 所在的平面 和圆O 所在的平面互相垂直,且 2AB , 1 EFAD . (Ⅰ)求证: AF 平面CBF ; (Ⅱ)设 FC 的中点为 M ,求证: //OM 平面 DAF ; (Ⅲ)设平面CBF 将几何体 EFABCD 分成的两个锥体的体积分别为 ABCDFV , CBEFV ,求 ABCDFV CBEFV : . 20.(本题满分 12 分)已知函数 dcxbxaxxf 23)( , )( Rx 在任意一点 ))(,( 00 xfx 处的切线的斜 率为 )1)(2( 00 xxk 。 (1)求 cba ,, 的值; (2)求函数 )(xf 的单调区间; (3)若 )(xfy 在 23 x 上的最小值为 2 5 ,求 )(xfy 在 R 上的极大值。 21.(本题满分 13 分) 如图,两条过原点O 的直线 21, ll 分别与 x 轴、y 轴成 30 的角,已知线段 PQ 的长度为 2 ,且点 ),( 11 yxP 在 直线 1l 上运动,点 ),( 22 yxQ 在直线 2l 上运动. (Ⅰ)求动点 ),( 21 xxM 的轨迹 C 的方程; (Ⅱ)设过定点 )2,0(T 的直线l 与(Ⅰ)中的轨迹 C 交于不同的两点 A 、 B ,且 AOB 为锐角,求直线l 的斜率 k 的取值范围. 22.(本小题满分 14 分) 设数列 na 的前 n 项和为 nS , 11 a ,且对任意正整数 n ,点 nn Sa ,1 在直线 022 yx 上. (Ⅰ)求数列 na 的通项公式; (Ⅱ)是否存在实数 ,使得数列 nn nS 2 为等差数列?若存在,求出 的 值;若不存在,则说明理由. (Ⅲ)求证: 2 1 )1)(1( 2 6 1 1 1 n k kk k aa . 2010 年高中文科数学高考模拟试卷 答案及评分标准 一、ABBCD DABCD CC 二、13. 20 . 14. 2[ , )4 . 15. 2 222 cba . 16. 8,2 3 . 三、解答题:本大题满分 74 分. 17.解:(Ⅰ)∵ 2( ) cos ( 3 cos sin ) 3sin sin cosf x x x x x x x 2 23(cos sin ) 2sin cosx x x x xx 2sin2cos3 )32sin(2 x . )(xf 的最小正周期为 . (Ⅱ)∵ ]2,3[ x , 3 4 323 x , ………… 9 分 又 )32sin(2)( xxf , ]2,3[)( xf , ( )f x 的值域为 ]2,3[ . 18.解:(Ⅰ)每颗骰子出现的点数都有 6 种情况,所以基本事件总数为 3666 个. 2 分 记“点 ),( yxP 在直线 1 xy 上”为事件 A , A 有 5 个基本事件: )}5,6(),4,5(),3,4(),2,3(),1,2{(A , .36 5)( AP …… 5 分 (Ⅱ)记“点 ),( yxP 满足 xy 42 ”为事件 B ,则事件 B 有17 个基本事件: 当 1x 时, ;1y 当 2x 时, 2,1y ; …………… 6 分 当 3x 时, 3,2,1y ;当 4x 时, ;3,2,1y ……………… 8 分 当 5x 时, 4,3,2,1y ;当 6x 时, 4,3,2,1y . .36 17)( BP ………… 10 分 19.(Ⅰ)证明: 平面 ABCD 平面 ABEF , ABCB , 平面 ABCD 平面 ABEF = AB , CB 平面 ABEF , AF 平面 ABEF , CBAF ,又 AB 为圆O 的直径, BFAF , AF 平面 CBF 。 …………………… 5 分 (Ⅱ)设 DF 的中点为 N ,则 MN // CD2 1 ,又 AO // CD2 1 , 则 MN // AO ,MNAO 为平行四边形, //OM AN ,又 AN 平面 DAF , OM 平面 DAF , //OM 平面 DAF 。 (Ⅲ)过点 F 作 ABFG 于G ,平面 ABCD 平面 ABEF , FG 平面 ABCD , FGFGSV ABCDABCDF 3 2 3 1 , CB 平面 ABEF , CBSVV BFEBFECCBEF 3 1 FGCBFGEF 6 1 2 1 3 1 , ABCDFV 1:4: CBEFV . 20.(本小题满分 12 分)解:(1) cbxaxxf 23)( 2 (1 分) 而 )(xf 在 ))(,( 00 xfx 处的切线斜率 )1)(2(23)( 000 2 00 xxcbxaxxfk ∴ 2,12,13 cba ∴ 3 1a , 2 1b , 2c (3 分) (2)∵ dxxxxf 22 1 3 1)( 23 由 0)1)(2(2)( 2 xxxxxf 知 )(xf 在 ]1,( 和 ),2[ 上是增函数 A B T y xo 由 0)1)(2()( xxxf 知 )(xf 在 ]2,1[ 上为减函数(7 分) (3)由 )1)(2()( xxxf 及 23 x 可列表 x )1,3[ 1 ]2,1( )(xf + 0 - )(xf 极大值 )(xf 在 ]2,3[ 上的最小值产生于 )3(f 和 )2(f 由 df 2 15)3( , df 3 10)2( 知 )2()3( ff (9 分) 于是 2 5 2 15)3( df 则 10d (11 分)∴ 6 67)1()( fxf 极大值 即所求函数 )(xf 在 R 上的极大值为 6 67 (12 分) 21.解:(Ⅰ)由已知得直线 21 ll , 1l : xy 3 3 , 2l : xy 3 , ……… 2 分 ),( 11 yxP 在直线 1l 上运动, ),( 22 yxQ 直线 2l 上运动, 11 3 3 xy , 22 3xy , …………………… 3 分 由 2PQ 得 4)()( 2 2 2 2 2 1 2 1 yxyx , 即 443 4 2 2 2 1 xx , 13 2 2 2 1 xx , …………………… 4 分 动点 ),( 21 xxM 的轨迹C 的方程为 13 2 2 yx . …………………… 5 分 (Ⅱ)直线l 方程为 2 kxy ,将其代入 13 2 2 yx , 化简得 0912)31( 22 kxxk , ……… 7 分 设 ),( 11 yxA 、 ),( 22 yxB 0)31(36)12( 22 kk , 12 k , 且 221221 31 9,31 12 kxxk kxxx , …………………… 9 分 AOB 为锐角, 0 OBOA , …………………… 9 分 即 02121 yyxx , 0)2)(2( 2121 kxkxxx , 04)(2)1( 2121 2 xxkxxk . 将 221221 31 9,31 12 kxxk kxxx 代入上式, 化简得 031 313 2 2 k k , 3 132 k . …………………… 11 分 由 12 k 且 3 132 k ,得 )3 39,1()1,3 39( k . ……………………13 分 22.(本小题满分 14 分) 设数列 na 的前 n 项和为 nS , 11 a ,且对任意正整数 n ,点 nn Sa ,1 在直线 022 yx 上. (Ⅰ) 求数列 na 的通项公式; (Ⅱ)是否存在实数 ,使得数列 nn nS 2 为等差数列?若存在,求出 的值;若不存在,则说明 理由. (Ⅲ)求证: 2 1 )1)(1( 2 6 1 1 1 n k kk k aa . 解:(Ⅰ)由题意可得: .022 1 nn Sa ① 2n 时, .022 1 nn Sa ② …………………… 1 分 ①─②得 22 1022 1 1 na aaaa n n nnn , 2 122,1 2121 aaaa …………………… 3 分 na 是首项为1,公比为 2 1 的等比数列, .2 1 1 n na ……………… 4 分 (Ⅱ)解法一: . 2 12 2 11 2 11 1 n n nS ……………… 5 分 若 nnS 2 为等差数列, 则 33221 2 3, 2 2,2 SSS 成等差数列, ……………… 6 分 2 ,8 25 4 7 2 314 9 2 328 25 2 3 4 9 312 SSS 得 .2 ……………… 8 分 又 2 时, 22 2 22 nnS nn ,显然 22 n 成等差数列, 故存在实数 2 ,使得数列 nn nS 2 成等差数列. ……………… 9 分 解法二: . 2 12 2 11 2 11 1 n n nS ……………… 5 分 . 2 122 22 12 2 1 nnnnn nnnS …………… 7 分 欲使 nn nS 2 成等差数列,只须 02 即 2 便可. ……………8 分 故存在实数 2 ,使得数列 nn nS 2 成等差数列. ……………… 9 分 (Ⅲ) )1)(1( 1 1kk aa ( 2 1 )1 2 1)(1 2 1( 1 1 k kk 1 2 1 1 k ) 1 2 1 1 1 k …… 10 分 n k k n k ktk k aa 11 1 1 2 1 1()1)(1( 2 ) 1 2 1 1 1 k ………… 11 分 )11 1 12 1 1( ) 12 1 1 12 1 1( 2 1 2 1 1( t ) 1 2 1 1 1 k 11 1 1 2 1 1 k 2 1 12 2 k k ………… 12 分 又函数 12 2 x x y 1 2 1 1 x 在 ),1[ x 上为增函数, 1 12 2 12 2 1 1 k k , ………… 13 分 2 112 1 12 2 2 1 3 2 k k , 2 1 )1)(1( 2 6 1 1 1 n k kk k aa . ……… 14 分 向你推荐高考状元复习法: 朱坤(北京大学光华管理学院学生,河南省高考文科状元): 数学是我最讨厌,也是最头疼的科目之一。不过,它对于文科生又至关重要,成为衡 量优秀学生与一般学生的最重要的尺度。我高一高二时,数学基础不好,时常不及格, 因此心里对它实在是有些害怕。高三数学复习要经过三轮,第一轮先将各知识点重讲 一遍,第二轮将各个知识点串联起来,比较有系统性,第三轮则是做综合试题。每一 轮都离不了大量的题目,如若题题都做,实在精力不逮,况且其他几科的复习又都如 箭在弦上,不得不发,因此事实上我做的题目连 20%也没有。我更注重于对各个知识 点的理解,只有理解了才会运用,这是很明显的道理,况且高考试题又都不是很难, 花费大量时间去钻所谓难题以提高能力实在不值得去效仿。做数学题比做其他题更注 重技巧,比如数学中的解答题,参考答案标明了每一步骤各有多少分,少一个步骤就 要丢掉多少多少分,实在很可惜。我做题就是步骤尽可能的繁复,以期别人抓不到破 绽。我觉得这个方法还蛮有用。再有就是碰到过难的题,也要尽量多写;实在写不下 去,只好胡猜一个结果,以图侥幸。至于有些选择题、填空题技巧,一般老师都多有 秘诀,我在这儿就不多说了。 胡湛智(北京大学生命科学学院学生,贵州省高考理科状元): 数学是理科的支柱,数学基础不好往往影响到理化成绩的提高,因此必须给予足够的 重视。高中的数学可以分为几个大的“板块”:一是函数板块,二是三角板块,三是 立体几何板块,四是解析几何板块,五是数列极限板块,六是排列组合板块,七是复 数板块。其中第一、二、四板块是尤其重要的,比较难的大题大多出自这三块,因此 可以多花一些力气。复习时可以先按照大的板块复习,争取搞清每一个板块的各种题 型,并做到能熟练地对付每种题型。这可以找一本系统复习的参考书来练习,最好是 能跟上老师复习的进度并稍超前些,复习起来就比较轻松了。虽然大家都不提倡“题 海战术”,我也不主张,那太费精力,但这并不意味着不做足够数量的习题就能把数 学学好,这一点必须引起注意。买的参考书和老师布置的习题一定要尽自己的力量做, 空着不做会留下遗憾的空白。关于做题难度的选择问题,我有一点自己的看法。首先, 高考题的难度分布为 30%的简单题,50%的中等题,20%的难题。这意味着基础题占了 120 分,它是复习中练题的主要部分,决不能厌烦它。要知道,高考不仅考你对知识 的掌握程度,还要考做题的速度,许多同学就是在高考时因时间不够,丢掉了平时能 做出来的中等难题才考砸的,这些教训值得大家三思。 鉴于此,我建议大家在中等以下难度的题上多花时间。做难题并非做得越多越好,只 能根据自己的情况适量地做:这一是因为对大多数同学来说做难题感到很头疼,容易 产生厌烦情绪;二是做难题过多太费时间;三是因为大多数难题是由中等难度题组成 的,基础题做熟练了,再来做难题会相对容易些。我的数学老师说过一句话:“越是 表面复杂的题越有机可乘”。这句话非常有道理,而高考的难题绝大部分就属于这种 表面复杂的类型,它往往给出较多的条件,仔细分析条件的特点通常都能击破它。做 难题的关键在于平时总结,自己总结一些小经验、小结论并记牢是非常有用的,能力 也提高得快,有余力的同学不妨试试。 另外,还要特别重视画图的作用。数学中几乎所有的内容都可以用图形给予直观简明 的表示,因而常使繁琐的题目简单化;特别地,通过图形发现的一些几何关系有时正 是解题的关键,因此要掌握各种函数图象的特点,达到熟练的程度。 邓芳(北京大学法律系学生,江西省高考文科状元): 数学相对文科生来说则属于偏理的科目,因此也是很多文科生的弱项。所以,学好数 学在激烈的高考竞争中是占有极大优势的。我觉得,学数学首先要掌握基本的公式、 原理,其次就要懂得灵活运用。第一步背公式,稍花点功夫大家都能做到,而要学会 灵活运用公式、原理解题则需要一定的训练。我的意思不是搞“题海”战术,题目是 永远都做不完的。我认为,除了老师布置的作业和学校发的卷子,只要适当精选一两 本课外参考书就够了。有些人买一大堆参考书,结果手忙脚乱做不过来,到处象征性 地“蜻蜒点水”一下,最终还是一无所获。与其这样,还不如集中精力吃透一本参考 书的效果好。学习数学,思考总结非常重要。很多人做题象完成任务似的,做完就不 管了。还有的人一旦做出一道难题就欣喜异常、大受鼓舞;想乘胜追击解出下一道难 题,因而又把做出的那道题扔在了一边。这两种做法是十分不可取的。我们每做一道 题都要注意思考总结,做完之后回想一下自己的解题思路,从中总结出这一类型题目 的一般解法,尤其是做完了难题,更应从中掌握这种题的特殊技巧。对于错题和没做 出来的题,则要搞懂答案的解题思路,并和自己的思维方法作对比,看看问题出在哪 一环。只有这样,做过的题才算真正消化吸收,变成了你自己的东西,否则下次碰到 同类的题又束手无策,那就白练习了。 所以,学数学主要就在背熟公式、原理的基础上,通过典型的例题的训练,从中掌握 一些题型的基本解法和某些特殊技巧,以不变应万变。另外,在练习过程中要重视基 础题,不能光想攻克难题,钻牛角尖。因为试卷上的难题毕竟不多,大多数还是容易 题和中等题,而且有些难题也只是在基础题上稍作变化而已。 2007 年高考数学试题分析—高中文科数学复习资料 摘要:二、复习方法建议 (一)总要求 1. 指导思想 准确标高,夯实基础;强 化过手,狠抓落实;突出思想,发展思维;分层推进,全面提高。 2. 总体策略 (1) 找准目标,分层推进的策略 普通高中有各种各样的层次,各自 ... 二、复习方法建议 (一)总要求 1. 指导思想 准确标高,夯实基础;强化过手,狠抓落实;突出思想,发展思维;分层推进,全面 提高。 2. 总体策略 (1)找准目标,分层推进的策略 普通高中有各种各样的层次,各自的目标,从而复习的起点、难度控制、方法与策略 都应有所不同。 (2)坚持扎实基础,提高能力并举的策略 数学试题区分度的增加是必然的,但考查基础的趋势是不会变的,主要是适当增加创 新成分,同时罩保留一定的基础分。 因此,基础题仍然是试题的主要构成,是学生得分的主要来源。 ①扎实基础是各个阶段复习的最重要策略 第一阶段复习要注意检查公式记忆是否落实;对教材中的基本概念、性质、限制条件、 图形等基础知识等也不能只布置,还要有检查。 第一阶段复习不能留下盲点,尤其要重视对教材中的阅读材料、想一想、实习作业、 补充例、习题和研究性课题等的复习。 ②坚持以中低档题为主的训练策略 第一轮复习的要点一是要对准 110 分,加强低、中档题的训练,尤其是对选择题和填 空题的训练;二是在“三基”的训练中,力求过手。 ③条件好的中学要适当注意训练材料的实践性、开放性、探究性的策略 学习方法 生源条件较好的学校还应注意探究性、应用性问题的训练。 (3)坚持提高复习课课堂效益的策略 3. 树立两个意识 (1)“平台”意识 即是关注学生已有的知识和经验。 (2)“抓分”意识 即各个复习阶段怎样让学生得分的目标要拒体、要落实。 4. 做到三个回归 数学总复习一般要经历三个阶段: (1)系统复习阶段; (2)专题复习阶段; (3)综合训练(适应性训练)阶段。 在每个阶段都要做到三个回归,即“回归教材,回归基础,回归近几年的高考题”。 (二)拒体要求 (Ⅰ)明确复习的作用 1.深化对“三基”的理解、掌握和运用 高考试题改革的重点是:从“知识立意”向“能力立意”转变。考试大岗提出的数学 学科能力要求是:能力是指思维能力、运算能力、空间想象能力以及实践能力和创新 意识。 摘要: 新课标提出的数学学科的能力为:数学地提出问题、分析问题和解决问题的能 力,数学探究能力,数学建模能力,数学交流能力,数学实践能力,数学思维能力。 学习方法 2. 形成有效的知识网络 知识网络:就是知识之 ... http://www.35di.cn/index.php/huati/view/cps-2/id-44830查看更多