中考数学圆的有关性质押轴题专练

中考数学圆的有关性质押轴题专练

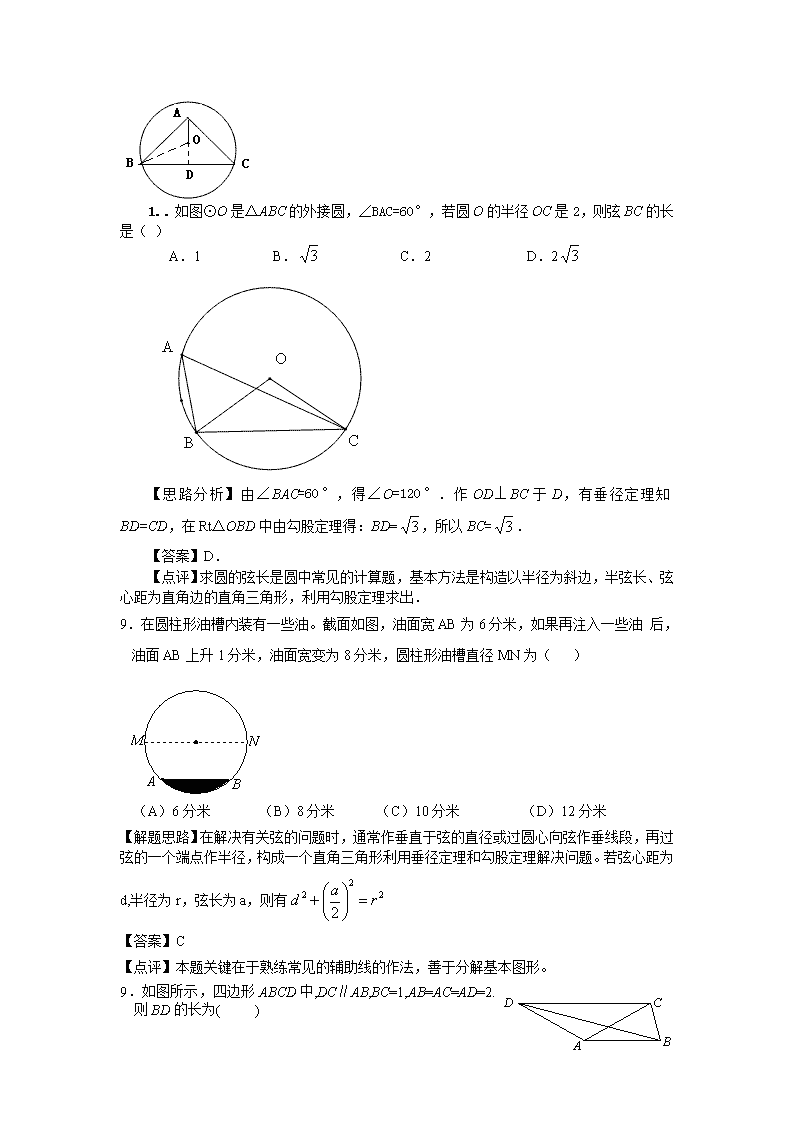
‎ 圆的有关性质 一、选择题 ‎1.如图，海边有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°，为了避免触礁，轮船P与A、B的张角∠APB的最大值为______°．‎ A B O P ‎(第12题)‎ ‎【解题思路】为了避免触礁，轮船P要在以A、B两点形成的的弓形上及以外区域活动，所以当P在弓形上时，轮船P与A、B的张角∠APB的最大，为400。‎ ‎【答案】400。‎ ‎【点评】此题能体现数学的应用价值，难道较较小。‎ 如图，点A、B、C在上，若，则的度数为（ ）‎ A. B. C. D. ‎ ‎【解题思路】和为同弧所对的圆心角与圆周角，根据圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半，可易得答案 ‎【答案】C ‎ ‎【点评】本题考查了圆周角定理的内容，属于基础题，难度较小。注意要正确的区分圆心角和圆周角。‎ ‎1.如图，直径为10的⊙A经过点C(0,5)和点O (0,0)， B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为( ) . ‎ D ‎ A． B． C． D．‎ ‎【解题思路】连接CD，则∠OBC=∠ODC，∵∠COD=90°，∴CD为直径=10，cos∠OBC =cos ‎∠ODC === ，选C. ‎ ‎【答案】C.‎ ‎【点评】本题在平面坐标系中，综合地考查同弧所对的圆周角相等、90°圆周角所的弦是直径、三角函数的定义等知识，解题的关键是能将∠OBC转移到直角三角形中去.难度中等.‎ ‎2.如图，将半径为‎2cm的圆形纸片折叠后，‎ 圆弧恰好经过圆心O，则折痕AB的长为( )‎ ‎ ‎ ‎ A、‎2cm B、cm C、cm D、cm ‎【解题思路】过O作OC⊥AB,垂足为C,连结OA,由垂径定理可得AC=CB.由已知得OC=,‎ 在Rt△AOC中，由勾股定理得cm.‎ ‎【答案】B ‎【点评】本题考查圆的有关性质中的垂径定理知识点，解有关弦长问题的关键是利用半径、弦心距、弦长构造直角三角形，再运用勾股定理。难度中等。‎ ‎3.如图，⊙O过点B、C，圆心O在等腰Rt△ABC的内部，∠BAC=90°，OA=1，BC=6.则⊙O的半径为 A. 6 B. ‎13 C. D. ‎ A B C O ‎【解题思路】因为△ABC是等腰直角三角形，过点A作AD⊥BC,垂直为D，则AD必过圆心O，连结0B.根据垂径定理，BD==3，AD=BD=3，OD=AD-OA=2.在Rt△BOD中，由勾股定理可求得OB=，故选C，显然其它选项不正确.‎ ‎【答案】C．‎ ‎【点评】本题考查的知识点垂径定理、勾股定理、等腰直角三角形的性质等知识点．解决问题的突破点是作弦心距或作等腰直角三角形斜边上高，连结OB，构建直角三角形利用勾股定理.难度中等．‎ ．如图⊙O是△ABC的外接圆，∠BAC=60°，若圆O的半径OC是2，则弦BC的长是（ ）‎ ‎ A．1 B． C．2 D．2‎ ‎【思路分析】由∠BAC=60°，得∠O=120°．作OD⊥BC于D，有垂径定理知BD=CD，在Rt△OBD中由勾股定理得：BD=，所以BC=．‎ ‎【答案】D．‎ ‎【点评】求圆的弦长是圆中常见的计算题，基本方法是构造以半径为斜边，半弦长、弦心距为直角边的直角三角形，利用勾股定理求出．‎ ‎9．在圆柱形油槽内装有一些油。截面如图，油面宽AB为6分米，如果再注入一些油 后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为（ ）‎ ‎（A）6分米 （B）8分米 （C）10分米 （D）12分米 ‎【解题思路】在解决有关弦的问题时，通常作垂直于弦的直径或过圆心向弦作垂线段，再过弦的一个端点作半径，构成一个直角三角形利用垂径定理和勾股定理解决问题。若弦心距为d,半径为r，弦长为a，则有 ‎【答案】C ‎【点评】本题关键在于熟练常见的辅助线的作法，善于分解基本图形。‎ A B C D ‎9．如图所示，四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为( )‎ A. B. C. D.‎ ‎【解题思路】由AB=AC=AD=2得,当以点为圆心,长为半径作圆,必经过,作直径,连接,由DC∥AB得,从而得到，在中，由勾股定理可求出的长.‎ ‎【答案】B ‎【点评】构造圆是本题的亮点和难点,到定点的距离等于定长的点的轨迹是以定点为圆心,定长为半径的圆,利用直径对直角构造直角三角形，丰富了试题的载体,难度较大.‎ ‎1.如图（5），△ABC内接于⊙O，若∠B=30°，AC=，则⊙O的直径为 ‎ 图（5）‎ O C B A 图（5）‎ O C B A A ‎【解题思路】连接AO、CO，则∠AOC=2∠B=60°，因为AO=CO，所以△AOC是等边三角形，所以OA= AC=，所以⊙O的直径为．‎ ‎【答案】‎ ‎【点评】由一般三角形中的圆周角转变为等腰三角形中的圆心角，这是正常思路，本题正好得等边△AOC．本题也可将30°的圆周角转化到直角三角形中，辅助线方面值得总结．‎ ‎9．如图， AB 为 ⊙ O 的直径， CD 为弦， AB ⊥ CD ，如果∠BOC = 70，那么∠A的度数为（ ） ‎ A．‎70 ‎ B．‎30‎ C．35 D． 20‎ ‎【解题思路】连接OD,由垂径定理得弧BC等于弧BD,再由“同圆中等弧所对的圆心角相等”得∠BOD＝∠BOC＝70°，最后由“同弧所对圆周角等于它所对圆心角的一半”，得∠A=∠BOD =35°．故选C．‎ ‎【答案】C．‎ ‎【点评】本题主要考查垂径定理及圆周角定理，是圆中典型的角度计算问题的综合，解决本题的关键是理解掌握圆中的垂径定理及圆周角定理，难度中等.‎ ‎2.如图(六)，△ABC的外接圆上，AB、BC、CA三弧的度数比为12：13：‎ ‎11。自BC上取一点D，过D分别作直线AC、直线AB的并行线，且交于E、F两点，则 ‎∠EDF的度数为何？‎ ‎(A) 55 (B) 60‎ ‎(C) 65 (D) 70‎ ‎【分析】：∵AB∥DF AC∥DE ∴∠B=∠DFE ∠C=∠CED ∴∠D=∠A，∵AB、BC、‎ CA三弧的度数比为∴∠A=‎ ‎【答案】：C ‎【点评】：本题考查了平行线的性质、三角形内角和定理、圆周角等知识。难度中等 ‎3.如图(十三)，ΔABC中，以B为圆心，长为半径画弧，分别交、‎ 于D、E两点，并连接、。若∠A=30∘，＝，则∠BDE的度数为何？‎ ‎(A) 45 (B) 52.5 (C) 67.5 (D) 75‎ ‎【分析】：∵AB=AC ∠A=300 ∴∠ABC=∠ACB= ∵BD=BC ∴∠DBC=30∘，∴∠EBD= ∵‎ BD=BE ∴∠BDE=67.5‎ ‎【答案】：C ‎【点评】：本题考查了等腰三角形，三角形内角和，圆的相关知识.难度较小.‎ ‎4.如图(十五)，为圆O的直径，在圆O上取异于A、B的一点C，并 连接、。若想在上取一点P，使得P与直线BC的距离等于长，判断下列四 个作法何者正确？‎ ‎(A)作的中垂线，交于P点 ‎(B)作∠ACB的角平分线，交于P点 ‎(C)作∠ABC的角平分线，交于D点，过D作直线BC的并行线，交于P点 ‎(D)过A作圆O的切线，交直线BC于D点，作∠ADC的角平分线，交于P点 ‎【分析】：过A作圆O的切线，交直线BC于D点，作∠ADC的角平分线，利用角平分线的性 质定理，可解。‎ ‎【答案】：D ‎【点评】：本题间接考察了角平分线性质定理，穿插了切线的性质（过半径的端点并与半径 垂直。难度较大。‎ ‎6．如图（3），CD是⊙O的弦，直径AB过CD的中点M，若∠BOC=40°，则∠ABD=‎ ‎(A) 40° (B) 60° （C）70° （D）80°‎ ‎【解题思路】：根据图（3）可得：∵CD是⊙O的弦，直径AB过CD的中点M，∴AB⊥CD, =,又∵∠BOC=40°，∴∠CDB=200，∴∠ABD,900-200=700.故C正确。‎ ‎【答案】C。‎ ‎【点评】本题是对垂径定理及圆心角与圆周角关系定理的考查，解决本题的关键是分析图形，确定垂直、平分关系，找准同弧或等弧所对的圆心角和圆周角，利用定理列出关系式，代值计算。本题难度中等。‎ 二、填空题 ‎5.如图，⊙O是的外接圆，CD是直径，，则的度数是 ▲ .‎ ‎【解题思路】连接AD，可得，,所以 ‎【答案】50°‎ ‎【点评】圆周角定理及其推论是中考命题的一个特点，因此，我们一定要理解同弧所对的圆周角的关系与直径所对的圆周角是直角，并注意灵活运用.‎ ‎19如图3所示，若⊙O的半径为‎13cm，点是弦上一动点，且到圆心的最短距离为‎5 cm，则弦的长为________cm．‎ 图3‎ ‎【解题思路】由点是弦上一动点，且到圆心的最短距离为‎5 cm，可知圆心o到弦AB的最小距离为‎5厘米，圆的半径为‎13厘米，根据垂径定理作OC⊥AB于C，连结OA，在Rt△AOC中，根据勾股定理知AC==12，所以AB=‎2AC=24．‎ ‎【答案】24．‎ ‎【点评】本题主要考察勾股定理和垂径定理．解题的关键是熟练地运用垂径定理并准确地作出辅助线．‎ ‎1.如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O 的半径是_________.‎ F G ‎ ‎ ‎【解题思路】过点O分别作OF⊥AB于F，OG⊥CD于G，∵AB⊥CD，AB=CD,∴四边形OFEG为正方形.由垂径定理得CG=DG==×（CE+DE）×（1+3）=2，∴OG=EG=CG-CE=2-1=1.连接OD，则OD==,即⊙O 的半径是.‎ ‎【答案】. ‎ ‎【点评】本题主要考查等弦的弦心距相等、垂径定理、勾股定理等有关知识，同时对矩形（正方形）的判定也有所涉及，是一道推理和计算相结合的较为常规的几何题.难度中等.‎ ‎2.如图，OB是⊙O的半径，点C、D在⊙O上，∠DCB=27°，则∠OBD=‎ ‎4. 度.‎ O D B C ‎【解题思路】∵∠DCB，∠DOB分别是 所对的圆周角和圆心角，∴∠DOB=2∠DCB=2×27°=54°，又∵OD=OB，∴∠OBD=（180°-54°）=63°．‎ ‎【答案】63 ．‎ ‎【点评】本题考查的是圆周角定理：同弧所对的圆周角是圆心角的一半．难度较小.‎ ‎3.如图，点E(0，4)，O(0，0)，C(5，0)在⊙A上，BE是⊙A上的一条弦，则tan∠OBE= ．‎ ‎【解题思路】连接E、C，则∠OBE=∠OCE，所以tan∠OBE=tan∠OCE==。‎ ‎【答案】‎ ‎【点评】本题主要考查与圆有关的计算，涉及到圆周角定理、三角函数等知识，此题的关键在于连接E、C将∠OBE转化为∠OCE。难度较小。‎ ‎4.如图，DE是⊙O的直径，弦AB⊥DE，垂足为C，若AB＝6，CE＝1，则OC＝__▲__，CD＝__▲__．‎ O E D C B A ‎【解题思路】连结OA．由垂径定理知AC＝3．设OC＝x，则OA＝x＋1．由勾股定理得(x＋1)2－x2＝32．解得x＝4．于是CD＝2x＋1＝9．‎ ‎【答案】4，9‎ ‎【点评】此题考查垂径定理和勾股定理等知识．此题的另一解法是：利用相似形得AC2＝CE·CD，从而先求出CD，然后再求OC的长，难度中等．‎ 如图，DE是⊙O的直径，弦AB⊥CD，垂足为C，若AB=6，CE=1，则OC= CD= 。‎ ‎·‎ D ‎ E ‎ A ‎ B ‎ O ‎ C ‎ ‎【解题思路】连接OA,设OA=x,则OC=x-1,由垂径定理有AC=AB=3，根据勾股定理：x2=32+(x-1)2,解得x=5,所以OC=4，OD=5.‎ ‎【答案】4；5.‎ ‎【点评】运用垂径定理解答问题时通常都是连接圆的半径，解答本题的关键是根据勾股定理建立方程使问题得以解决。‎ 如图，点D为AC上一点，点O为边AB上一点，AD＝DO．以O为圆心，OD长为半径作圆，交AC于另一点E，交AB于点F，G，连接EF．若∠BAC＝22°，则∠EFG＝_ ▲ ．‎ 第15题 ‎【解题思路】由AD＝DO，则∠BAC=∠DOA＝22°，则∠DEF=×22°=11°，由三角形的外角等于和它不相邻的两个内角和，得∠EFG＝33°.‎ ‎【答案】33°‎ ‎【点评】本题考查了等腰三角形的性质、圆心角与圆周角之间的关系、三角形的内、外角之间关系，有一定的综合性。难度中等。‎ 如图，以原点O为圆心的圆交x轴于A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=20°，则∠OCD= ▲ °．‎ ‎【解题思路】如图，连接OD，因为∠DAB=20°，所以∠DOB＝2∠DAB＝40°，所以∠DOE＝130°，∠OCD＝∠DOE＝65°.‎ ‎【答案】65‎ ‎【点评】本题主要考查与圆有关的弧、弧所对的圆周角、弧所对的圆心角，以及它们之间的数量关系，可以运用“一条弧所对的圆周角等于它所对的圆心角的一半”等定理求解.难度中等.‎ ‎1．如图，在⊙O中，直径CD垂直弦AB于点E，连接OB,CB，已知⊙O的半径为2，AB=,则∠BCD=________度．‎ ‎（第8题）‎ ‎【解题思路】：由直径CD垂直弦AB于点E，得BE=AB.在Rt△BOE中，利用锐角三角形函数可求出∠BOD的度数，再由圆周角定理求出∠BCD.‎ ‎【答案】30‎ ‎【点评】：本题涉及的知识点较多，理清题目中的数量关系，找出要求的量与已知量之间的关系是解题的关键 ‎2．如图5，⊙O的直径CD过弦EF的中点G，∠EOD=400 ，则∠FCD的度数为 ．‎ ‎【解题思路】连结OF，由题设⊙O的直径CD过弦EF的中点G，可得,所以∠FOD=∠EOD=400 ，根据一条弧所对的圆周角等于它所对的圆心角的一半可得∠FCD=200‎ ‎【答案】200‎ ‎【点评】由垂径定理可得：一条直线若满足①过圆心；②垂直于弦；③平分弦；④平分弦所对的优弧；⑤平分弦所对的劣弧中的任意两个条件，就可以推出其余三个结论．由此可得直径CD平分劣弧．‎ 三、解答题 ‎1. 如图,等腰梯形ABCD中,AB∥CD,AD=BC.将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合． ‎ ‎ (1)点C是否在以AB为直径的圆上?请说明理由; ‎ ‎ (2)当AB=4时,求此梯形的面积．‎ ‎ ‎ ‎【解题思路】（1）要判断点C是否在以AB为直径的圆上，只要判断点C到线段AB中点 M的距离CM是否为线段AB的一半，（2）作梯形ABCD的高DE，求出上底CD和高DE的长，代入梯形的面积公式即可求得.‎ ‎【答案】（1）点C在以AB为直径的圆上.‎ 理由：连接MC,MD,‎ ‎∵AB∥CD,∴∠DCA=∠BAC,‎ ‎∵∠DAC=∠BAC, ∴∠DAC=∠DCA, ∴AD=CD,‎ ‎∵AD=AM, ∴CD=AM, ‎ ‎∴四边形AMCD是平行四边形，∴MC=AD,‎ 同理MD=BC, ∵AD=BC, ∴MC=MD=AD=BC=MA=MB,‎ ‎ ∴点C在以AB为直径的圆上.‎ ‎(2)由（1）得△AMD是等边三角形，过点D作DE⊥AB于E,‎ 由勾股定理得，DE=,∴梯形ABCD的面积=.‎ ‎【点评】本题考查了点与圆的位置关系、勾股定理及梯形的面积公式，关键是证点C到线段AB中点M的距离CM为线段AB的一半及求上底CD和高DE长，难度较大.‎ ‎2.‎ ‎6.在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．‎ ‎⑴求证△ABD为等腰三角形．‎ ‎⑵求证AC•AF=DF•FE ‎【解题思路】（1）利用同角的补角相等，同弧所对的圆周角相等，等量代换；‎ ‎（2）证等积式就要找三角形相似，发现AC、AF、FE所在的三角形，且利用等弧对等弦，同圆中等弦对等弧，发现DF可以被DC替换，进而求解。‎ ‎【答案】⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA，而∠MCD=∠DCA，所以∠DBA=∠DAB，故△ABD为等腰三角形．‎ ‎⑵∵∠DBA=∠DAB ‎∴弧AD=弧BD 又∵BC=AF ‎∴弧BC=弧AF、∠CDB=∠FDA ‎∴弧CD=弧DF ‎∴CD=DF 再由“圆的内接四边形外角等于它的内对角”知 ‎∠AFE=∠DBA=∠DCA①，∠FAE=∠BDE ‎∴∠CDA=∠CDB＋∠BDA=∠FDA＋∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE ‎∴AC：FE=CD：AF ‎∴AC•AF= CD •FE 而CD=DF，‎ ‎∴AC•AF=DF•FE ‎【点评】解决此题关键要用到与圆相关的性质、定理以及三角形相似的判定，等角对等边。‎ 有一定的几何知识的综合性。考查学生审图，分析图中边角关系的解题技能。难度中等 ‎（2011江苏泰州，26，10分）如图，以点O为圆心的两个同心圆中，矩形ABCD的边BC为大圆的弦，边AD与小圆相切于点M，OM的延长线与BC相交于点N。‎ ‎（1）点N是线段BC的中点吗？为什么？‎ ‎（2）若圆环的宽度（两圆半径之差）为‎6cm，AB=‎5cm，BC=‎10cm，求小圆的半径。‎ ‎【解题思路】（1）根据切线的性质可得OM⊥AD，而AD∥BC，从而ON⊥BC，而BC是大圆的弦，根据垂径定理可得ON平分BC；（2）连接OC，构造直角三角形，利用勾股定理列方程可解。‎ ‎【答案】解：（1）是中点。‎ 矩形ABCD中，AD∥BC ‎∴∠OMD=∠ONC ‎∵AD切小圆与M ‎∴∠OMD=90°，∴∠ONC=90°‎ ‎∴ON平分BC，即N为BC的中点。‎ ‎（2）连接OC，设小圆半径为r，则大圆半径为（6+r）cm，‎ 由（1）得∠ONC=90°，而矩形ABCD中∠A=∠B=90°，所以四边形ABNM为矩形。‎ ‎∴MN=AB=‎5cm，‎ ‎∴ON=（5+r）cm。‎ 由（1）得NC==‎ 由Rt△ONC中，可得 ‎（5+r）2+52=(6+r)2 ，解得r=7‎ 答：小圆的半径为‎7cm。‎ ‎【点评】本题主要考查了与圆有关的图形的性质及其应用，切线的性质和垂径定理都是常见的考点，求与圆有关的线段长，往往需要构造直角三角形。新课程标准对圆的要求已经降低，所以本题的设计也是重在基础。难度中等。‎ 如图，⊙O的弦CD与直径AB相交，若∠BAD=50°，则∠ACD= .‎ ‎【解题思路】因为AB是⊙O的直径，所以∠ADB=90°，又因为∠BAD=50°，所以∠B=40°，根据同弧所对的圆周角相等，所以∠ACD=40°．‎ ‎【答案】40°．‎ ‎【点评】本题综合考查了圆的有关性质：“直径所对的圆周角是90°”及“同弧或等弧所对的圆周角相等”．‎ ‎26．如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD.‎ ‎（1）弦长AB等于 （结果保留根号）；‎ ‎（2）当∠D=20°时，求∠BOD的度数；‎ ‎（3）当AC的长度为多少时，以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似？‎ 请写出解答过程.‎ ‎【解题思路】(1)过点O作OE⊥AB于E，根据∠B=30°，OB=2，‎ 可得BE=，由垂径定理知AB=2；（2）连接AO，利用半径相等，‎ 可得∠BAD=∠BAD﹢∠BAD=50°；（3）由∠BCD是△ADC的外角，可知 ‎∠BCD≠∠CAD，∠BCD≠∠D，只有∠BCD=∠ACD，即∠BCD=∠ACD=90°‎ 由∠B=30°，得∠BOD=120°，由圆周角知∠CAD=60° ，可得△DAC∽△BOC，‎ AC=AB=.‎ ‎【解答】（1）2 ‎ ‎ （2）如图。连接OA.‎ ‎∵OA=OB，OA=OD， ∴∠BAO=∠B，∠DAO=∠D ‎∴∠DAB=∠BAO﹢∠DAO=∠B﹢∠D.‎ 又∵∠B=30°，∠D=20°，∴∠DAB=50°.‎ ‎∠BOD=2∠DAB=100°.‎ ‎（3）∵∠BCO=∠A﹢∠D，∠BCO>∠A，∠BCO>∠D ‎ ∴要使△DAC与△BOC相似，只能∠DCA=∠BCO=90°.‎ ‎ 此时∠BOC=60°，∠BOD=120°，∴∠DAC=60°.‎ ‎ ∴△DAC∽△BOC ‎ ∵∠BCO=90，即OC⊥AB，∴AC=AB=.‎ ‎【点评】圆中的圆周角定理、垂径定理在与圆有关的证明、计算题中经常出现，要牢固掌握.‎ ‎1.如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=40°，∠APD=65°.‎ ‎（1）求∠B的大小；‎ A C D B O ‎·‎ P E ‎（2）已知圆心O到BD的距离为3，求AD的长.‎ A C D B O ‎·‎ P ‎ 【解题思路】‎ ‎（1）根据同弧所对的圆周角相等，‎ 有∠B=∠CAB=40°，再由∠APD是 ‎△PBD的外角，于是可求出∠B的大小；‎ ‎ （2）OE过圆心且垂直于弦BD，根 据垂径定理所知，点E是BD中点，判 断出OE是△ABD中位线，最后根据中 位线性质可求得AD长.‎ ‎【答案】解：（1）∵∠APD是△APC的外角，∴∠APD=∠CAP+∠C.∴∠C=∠APD-∠CAP=65°-40°=25°.又∵，∴∠B=∠C=25°.‎ ‎（2）过点O作OE⊥BD，垂足为E，则OE=3.由垂径定理可知BE=DE.∵OA=OB.∴线段OE是△ABD的中位线.∴AD=2OE=6.‎ ‎【点评】本题考查了圆周角性质、三角形外角、三角形中位线定义及其性质等知识.突出考查了新课标要求的核心内容.较好地实现了注重基础、考查能力的目的.难度中等.‎ ‎2.如图，等边△ABC内接⊙O，P是上任一点（点P不与点A、B重合）.连AP、BP，过点C作CM∥BP交PA的延长线于点M.‎ ‎（1）填空：∠APC=________ 度，∠BPC________ 度.‎ ‎（2）求证：△ACM≌△BCP.‎ ‎（3）若PA=1，PB=2，求梯形PBCM的面积 ‎【解题思路】对于（1）,利用同弧所对的圆周角相等即可得到两个角的度数;对于(2),根据平行及(1)中∠APC=60°,可得到△PCM为等边三角形,再用AAS证明全等;(3)要求梯形PBCM的面积,上底=BP=2,再结合(2)中的结论,可知CM=PM=PA+AM=PA+PB=1+2=3,所以,求高是关键.‎ ‎【答案】解：（1）60，60.‎ ‎（2）∵CM∥BP,∴∠BPM+∠M=180°，∠PCM=∠BPC=60°，∴∠M=180°-∠BPM =180°-（∠APC+∠BPC）=180°-120°=60°.∴∠M=∠BPC=60°.又△ABC为等边三角形，∴BC=AC，∠CAB=60°，∴∠PCM-∠ACP=∠BCA-∠ACP,即∠ACM=∠BCP.在△ACM和△BCP中 ‎∠M=∠BPC,‎ ‎∠ACM=∠BCP,‎ AC=BC,‎ ‎∴△ACM≌△BCP.‎ ‎（3）∵△ACM≌△BCP,‎ ‎ ∴CM＝CP ,AM=BP.‎ 又∠M=60°，∴△PCM为等边三角形.‎ ‎∴CM=CP=PM=1+2=3.‎ 作PH⊥CM于H.‎ 在Rt△PMH中，∠MPH=30°∴PH=.‎ ‎∴S四边形PBCM=.‎ ‎【点评】本题以圆为背景,重点考查了圆周角定理以及推论,全等的判定以及梯形和解直角三角形等．难度中等．‎ ‎3．在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．‎ ‎⑴求证△ABD为等腰三角形．‎ ‎⑵求证AC•AF=DF•FE ‎ 第22题图 B A F E D C M ‎【思路分析】（1）利用圆内接四边的性质可得∠MCD=∠DAB，由同弧或等弧所对的圆周角相等，可得∠DCA=∠DBA，由角平分线的定义可得∠MCD=∠DCA.所以∠DBA=∠DAB.所以△ABD为等腰三角形．‎ ‎（2）可通过证明△DCA∽△FAE即可.‎ ‎【答案】⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA，而∠MCD=∠DCA，所以∠DBA=∠DAB，故△ABD为等腰三角形．‎ ‎⑵∵∠DBA=∠DAB，∴弧AD=弧BD，又∵BC=AF，∴弧BC=弧AF、∠CDB=∠FDA，‎ ‎∴弧CD=弧DF，∴CD=DF.‎ 再由“圆的内接四边形外角等于它的内对角”知 ‎∠AFE=∠DBA=∠DCA①，∠FAE=∠BDE，∴∠CDA=∠CDB＋∠BDA=∠FDA＋∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE，∴AC：FE=CD：AF，∴AC•AF= CD •FE，而CD=DF，∴AC•AF=DF•FE.‎ ‎【点评】本题主要考查了圆的内接四边形，相似三角形的判定和性质等知识点，通过构建相似三角形来来求解是解题的关键．难度中等.‎