【数学】2019届一轮复习人教A版(文)第三章第1节任意角和弧度制及任意角的三角函数学案
第一节任意角和弧度制及任意角的三角函数
1.角的概念的推广
(1)定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
(2)分类
(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+2kπ,k∈Z}.
2.弧度制的定义和公式
(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad.
(2)公式:
角α的弧度数公式
|α|=(l表示弧长)
角度与弧度的换算
①1°= rad;②1 rad=°
弧长公式
l=|α|r
扇形面积公式
S=lr=|α|r2
3.任意角的三角函数
(1)定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),那么sin α=,cos α=,tan α=(x≠0).
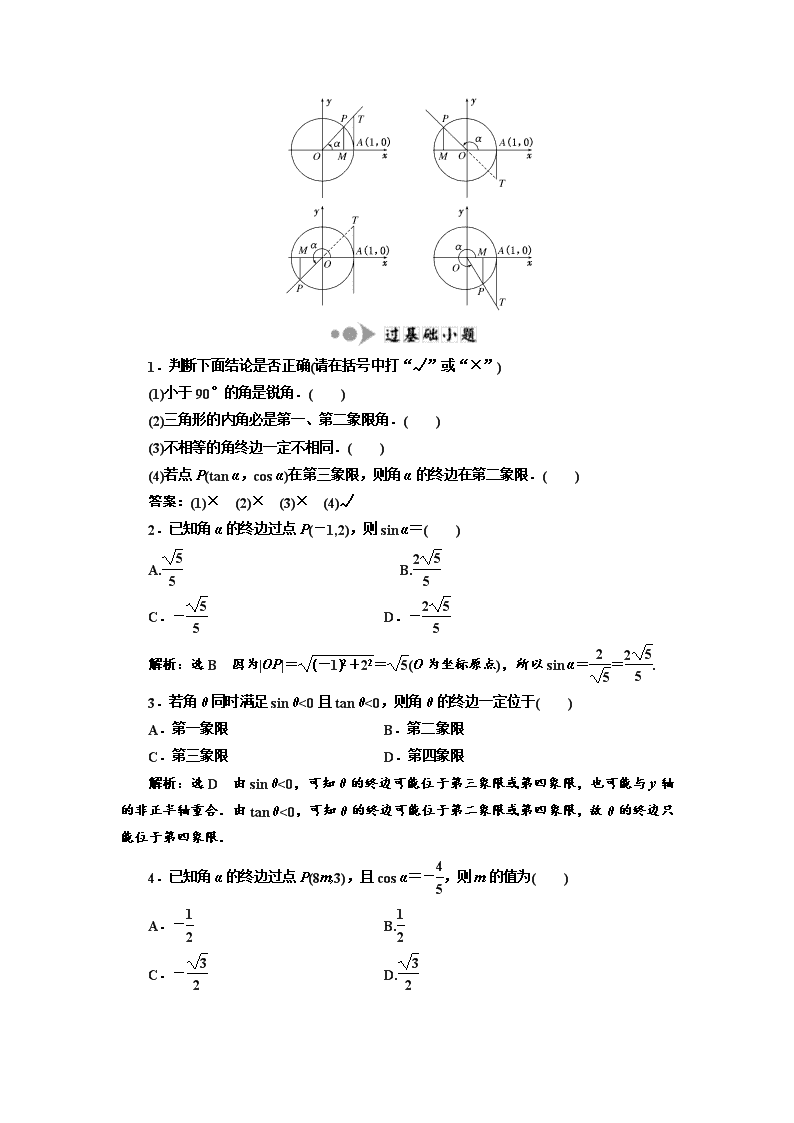
(2)几何表示:三角函数线可以看作是三角函数的几何表示.正弦线的起点都在x轴上,余弦线的起点都是原点,正切线的起点都是(1,0).如图中有向线段MP,OM,AT分别叫做角α的正弦线、余弦线和正切线.
1.判断下面结论是否正确(请在括号中打“√”或“×”)
(1)小于90°的角是锐角.( )
(2)三角形的内角必是第一、第二象限角.( )
(3)不相等的角终边一定不相同.( )
(4)若点P(tan α,cos α)在第三象限,则角α的终边在第二象限.( )
答案:(1)× (2)× (3)× (4)√
2.已知角α的终边过点P(-1,2),则sin α=( )
A. B.
C.- D.-
解析:选B 因为|OP|==(O为坐标原点),所以sin α==.
3.若角θ同时满足sin θ<0且tan θ<0,则角θ的终边一定位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:选D 由sin θ<0,可知θ的终边可能位于第三象限或第四象限,也可能与y轴的非正半轴重合.由tan θ<0,可知θ的终边可能位于第二象限或第四象限,故θ的终边只能位于第四象限.
4.已知角α的终边过点P(8m,3),且cos α=-,则m的值为( )
A.- B.
C.- D.
解析:选A 由题意得=-,且m<0.
解得m=-.
5.已知扇形的圆心角为60°,其弧长为2π,则此扇形的面积为________.
解析:设此扇形的半径为r,由题意得r=2π,所以r=6,
所以此扇形的面积为×2π×6=6π.
答案:6π
6.在0到2π范围内,与角-终边相同的角是________.
解析:与角-终边相同的角是2kπ+,k∈Z,令k=1,可得与角-终边相同的角是.
答案:
[考什么·怎么考]
高考对象限角及终边相同的角直接考查较少,多渗透到三角函数求值及性质中,属于基础题.
1.给出下列四个命题:
①-是第二象限角;
②是第三象限角;
③-400°是第四象限角;
④-315°是第一象限角.
其中正确命题的个数为( )
A.1 B.2
C.3 D.4
解析:选C -是第三象限角,故①错误;=π+,从而是第三象限角,故②正确;-400°=-360°-40°,从而-400°是第四象限角,故③正确;-315°=-360°+45°,从而-315°是第一象限角,故④正确,故选C.
2.在-720°~0°范围内所有与45°终边相同的角为________.
解析:所有与45°终边相同的角可表示为:
β=45°+k×360°(k∈Z),
则令-720°≤45°+k×360°<0°(k∈Z),
得-765°≤k×360°<-45°(k∈Z),
解得-≤k<-(k∈Z),
从而k=-2或k=-1,
代入得β=-675°或β=-315°.
答案:-675°或-315°
3.终边在直线y=x上的角的集合为__________________.
解析:在坐标系中画出直线y=x,可以发现它与x轴正半轴的夹角是,终边在直线y=x上的角的集合为.
答案:
4.若角α是第二象限角,则是第________象限角.
解析:∵α是第二象限角,∴+2kπ<α<π+2kπ,k∈Z,
∴+kπ<<+kπ,k∈Z.当k为偶数时,是第一象限角;当k为奇数时,是第三象限角.
答案:一或三
[怎样快解·准解]
1.象限角的两种判断方法
(1)图象法:在平面直角坐标系中,作出已知角并根据象限角的定义直接判断已知角是第几象限角.
(2)转化法:先将已知角化为k·360°+α(0°≤α<360°,k∈Z)的形式,即找出与已知角终边相同的角α,再由角α终边所在的象限判断已知角是第几象限角.
2.求或nθ(n∈N*)所在象限的方法
(1)将θ的范围用不等式(含有k,且k∈Z)表示.
(2)两边同除以n或乘以n.
(3)对k进行讨论,得到或nθ(n∈N*)所在的象限.
[注意] (1)相等的角终边一定相同,但终边相同的角却不一定相等,终边相同的角有无数个,它们之间相差360°的整数倍.
(2)终边在一条直线上的角之间相差180°的整数倍;终边在互相垂直的两条直线上的角之间相差90°的整数倍.
[考什么·怎么考]
高考对扇形的弧长、面积公式很少直接考查,主要是理解弧度制下的公式的应用,属于基础题.
1.已知扇形的周长是6,面积是2,则扇形的圆心角的弧度数是( )
A.1 B.4
C.1或4 D.2或4
解析:选C 设扇形的半径为r,弧长为l,
则解得或
从而α===4或α===1.
2.已知扇形弧长为20 cm,圆心角为100°,则该扇形的面积为________cm2.
解析:由弧长公式l=|α|r,得
r==,∴S扇形=lr=×20×=.
答案:
3.如果一个扇形的半径变为原来的一半,而弧长变为原来的倍,则该弧所对的圆心角是原来的________倍.
解析:设圆的半径为r,弧长为l,则其弧度数为.
将半径变为原来的一半,弧长变为原来的倍,
则弧度数变为=3·,
即弧度数变为原来的3倍.
答案:3
[怎样快解·准解]
弧度制下有关弧长、扇形面积问题的解题策略
(1)明确弧度制下弧长及扇形面积公式,在使用公式时,要注意角的单位必须是弧度.
(2)分析题目已知哪些量、要求哪些量,然后灵活地运用弧长公式、扇形面积公式直接求解,或合理地利用圆心角所在三角形列方程(组)求解.
任意角的三角函数(正弦、余弦、正切)的定义属于理解内容.在高考中多以选择题、填空题的形式出现.,常见的命题角度有:
(1)利用三角函数定义求值;
(2)三角函数值符号的判定;
(3)三角函数线的应用.
[题点全练]
角度(一) 利用三角函数定义求值
1.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos 2θ=( )
A.- B.-
C. D.
解析:选B 设P(t,2t)(t≠0)为角θ终边上任意一点,则cos θ=.
当t>0时,cos θ=;当t<0时,cos θ=-.
因此cos 2θ=2cos2θ-1=-1=-.
2.已知角α的终边经过点P(-x,-6),且cos α=-,则+=________.
解析:∵角α的终边经过点P(-x,-6),且cos α=-,
∴cos α==-,解得x=或x=-(舍去),
∴P,
∴sin α=-,∴tan α==,
则+=-+=-.
答案:-
[题型技法] 利用三角函数定义求三角函数值的方法
(1)已知角α终边上一点P的坐标,则可先求出点P到原点的距离r,然后用三角函数的定义求解.
(2)已知角α的终边所在的直线方程,则可先设出终边上一点的坐标,求出此点到原点的距离,然后用三角函数的定义求解.
角度(二) 三角函数值符号的判定
3.(2014·全国卷Ⅰ)若tan α>0,则( )
A.sin α>0 B.cos α>0
C.sin 2α>0 D.cos 2α>0
解析:选C 由tan α>0,可得α的终边在第一象限或第三象限,此时sin α与cos α同号,故sin 2α=2sin acos α>0,故选C.
4.若sin αtan α<0,且<0,则角α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
解析:选C 由sin αtan α<0可知sin α,tan α异号,
则α为第二象限角或第三象限角.
由<0可知cos α,tan α异号,
则α为第三象限角或第四象限角.
综上可知,α为第三象限角.
[题型技法] 三角函数值符号及角的位置判断
已知一角的三角函数值(sin α,cos α,tan α)中任意两个的符号,可分别确定出角终边所在的可能位置,二者的交集即为该角的终边位置,注意终边在坐标轴上的特殊情况.
角度(三) 三角函数线的应用
5.函数y=lg(3-4sin2x)的定义域为________.
解析:∵3-4sin2x>0,∴sin2x<,
∴-
1.
[冲关演练]
1.如图,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为,则cos α的值为( )
A. B.-
C. D.-
解析:选D 因为点A的纵坐标yA=,且点A在第二象限,又因为圆O为单位圆,所以A点的横坐标xA=-,由三角函数的定义可得cos α=-.
2.已知点P(cos α,tan α)在第三象限,则角α的终边在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:选B 由题意得⇒所以角α的终边在第二象限.
3.函数y= 的定义域为________.
解析:因为sin x≥,作直线y=交单位圆于A,B两点,连接OA,OB,则OA与OB围成的区域(图中阴影部分)即为角x的终边的范围,故满足条件的角x的集合为.
答案:,k∈Z
(一)普通高中适用作业
A级——基础小题练熟练快
1.已知扇形的面积为2,扇形圆心角的弧度数是4,则扇形的周长为( )
A.2 B.4
C.6 D.8
解析:选C 设扇形的半径为r,弧长为l,则由扇形面积公式可得2=lr=|α|r2=×4×r2,解得r=1,l=αr=4,所以所求扇形的周长为2r+l=6.
2.已知点P在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A. B.
C. D.
解析:选C 因为点P在第四象限,
根据三角函数的定义可知tan θ==-,
又θ∈[0,2π),可得θ=.
3.若角α与β的终边关于x轴对称,则有( )
A.α+β=90°
B.α+β=90°+k·360°,k∈Z
C.α+β=2k·180°,k∈Z
D.α+β=180°+k·360°,k∈Z
解析:选C 因为α与β的终边关于x轴对称,所以β=2k·180°-α,k∈Z.所以α+β=2k·180°,k∈Z.
4.已知角α的终边经过点(3a-9,a+2),且cos α≤0,sin α>0,则实数a的取值范围是( )
A.(-2,3] B.(-2,3)
C.[-2,3) D.[-2,3]
解析:选A 由cos α≤0,sin α>0可知,角α的终边落在第二象限或y轴的正半轴上,所以有
解得-2<a≤3.
5.下列选项中正确的是( )
A.sin 300°>0 B.cos(-305°)<0
C.tan>0 D.sin 10<0
解析:选D 300°=360°-60°,则300°是第四象限角;
-305°=-360°+55°,则-305°是第一象限角;
因为-=-8π+,所以-是第二象限角;
因为3π<10<,所以10是第三象限角.故sin 300°<0,cos(-305°)>0,tan<0,sin 10<0,故D正确.
6.集合中的角所表示的范围(阴影部分)是( )
解析:选C 当k=2n(n∈Z)时,2nπ+≤α≤2nπ+,此时α表示的范围与≤α≤表示的范围一样;当k=2n+1(n∈Z)时,2nπ+π+≤α≤2nπ+π+,此时α表示的范围与π+≤α≤π+表示的范围一样,结合图象知选C.
7.若α=1 560°,角θ与α终边相同,且-360°<θ<360°,则θ=________.
解析:因为α=1 560°=4×360°+120°,
所以与α终边相同的角为360°×k+120°,k∈Z,
令k=-1或k=0可得θ=-240°或θ=120°.
答案:120°或-240°
8.在直角坐标系xOy中,O是原点,A(,1),将点A绕O逆时针旋转90°到B点,则B点坐标为__________.
解析:依题意知OA=OB=2,∠AOx=30°,∠BOx=120°,
设点B坐标为(x,y),所以x=2cos 120°=-1,y=2sin 120°=,即B(-1,).
答案:(-1,)
9.若两个圆心角相同的扇形的面积之比为1∶4,则这两个扇形的周长之比为________.
解析:设两个扇形的圆心角的弧度数为α,半径分别为r,R(其中r<R),则=,
所以r∶R=1∶2,两个扇形的周长之比为=1∶2.
答案:1∶2
10.已知角α的终边上一点P(-,m)(m≠0),且sin α=,则m=________.
解析:由题设知点P的横坐标x=-,纵坐标y=m,
∴r2=|OP|2=(-)2+m2(O为原点),
即r=.
∴sin α===,
∴r==2,
即3+m2=8,解得m=±.
答案:±
B级——中档题目练通抓牢
1.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角α(0<α<π)的弧度数为( )
A. B.
C. D.
解析:选C 设圆的半径为R,由题意可知,圆内接正三角形的边长为R,所以圆弧长为R.所以该圆弧所对圆心角的弧度数为=.
2.已知角α=2kπ-(k∈Z),若角θ与角α的终边相同,则y=++的值为( )
A.1 B.-1
C.3 D.-3
解析:选B 由α=2kπ-(k∈Z)及终边相同的概念知,角α的终边在第四象限,又角θ与角α的终边相同,所以角θ是第四象限角,所以sin θ<0,cos θ>0,tan θ<0.
所以y=-1+1-1=-1.
3.设α是第二象限角,P(x,4)为其终边上的一点,且cos α=x,则tan α=( )
A. B.
C.- D.-
解析:选D ∵α是第二象限角,∴x<0.
又由题意知=x,
解得x=-3.
∴tan α==-.
4.一扇形是从一个圆中剪下的一部分,半径等于圆半径的,面积等于圆面积的,则扇形的弧长与圆周长之比为________.
解析:设圆的半径为r,则扇形的半径为,记扇形的圆心角为α,
则=,
∴α=.
∴扇形的弧长与圆周长之比为==.
答案:
5.(2018·石家庄模拟)在(0,2π)内,使sin x>cos x成立的x的取值范围为____________.
解析:如图所示,找出在(0,2π)内,使sin x=cos x的x值,sin=cos=,sin=cos=-.根据三角函数线的变化规律标出满足题中条件的角x∈.
答案:
6.已知=-,且lg(cos α)有意义.
(1)试判断角α所在的象限;
(2)若角α的终边上一点M,且|OM|=1(O为坐标原点),求m的值及sin α的值.
解:(1)由=-,得sin α<0,
由lg(cos α)有意义,可知cos α>0,
所以α是第四象限角.
(2)因为|OM|=1,所以2+m2=1,
解得m=±.
又α为第四象限角,故m<0,
从而m=-,
sin α====-.
7.若角θ的终边过点P(-4a,3a)(a≠0),
(1)求sin θ+cos θ的值;
(2)试判断cos(sin θ)·sin(cos θ)的符号.
解:(1)因为角θ的终边过点P(-4a,3a)(a≠0),
所以x=-4a,y=3a,r=5|a|,
当a>0时,r=5a,sin θ+cos θ=-=-.
当a<0时,r=-5a,sin θ+cos θ=-+=.
(2)当a>0时,sin θ=∈,
cos θ=-∈,
则cos(sin θ)·sin(cos θ)=cos ·sin<0;
当a<0时,sin θ=-∈,
cos θ=∈,
则cos(sin θ)·sin(cos θ)=cos·sin >0.
综上,当a>0时,cos(sin θ)·sin(cos θ)的符号为负;
当a<0时,cos(sin θ)·sin(cos θ)的符号为正.
C级——重难题目自主选做
已知扇形AOB的周长为8.
(1)若这个扇形的面积为3,求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.
解:设扇形AOB的半径为r,弧长为l,圆心角为α,
(1)由题意可得
解得或
∴α==或α==6.
(2)法一:∵2r+l=8,
∴S扇=lr=l·2r≤2=×2=4,
当且仅当2r=l,即r=2,l=4,α==2时,扇形面积取得最大值4.
∴圆心角α=2,弦长AB=2sin 1×2=4sin 1.
法二:∵2r+l=8,
∴S扇=lr=r(8-2r)=r(4-r)=-(r-2)2+4≤4,
当且仅当r=2,l=4,即α==2时,扇形面积取得最大值4.
∴弦长AB=2sin 1×2=4sin 1.
(二)重点高中适用作业
A级——保分题目巧做快做
1.下列与的终边相同的角的表达式中正确的是( )
A.2kπ+45°(k∈Z) B.k·360°+π(k∈Z)
C.k·360°-315°(k∈Z) D.kπ+(k∈Z)
解析:选C 由定义知终边相同的角中不能同时出现角度和弧度,应为+2kπ或k·360°+45°(k∈Z),结合选项知C正确.
2.已知点P在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A. B.
C. D.
解析:选C 因为点P在第四象限,
所以根据三角函数的定义可知tan θ==-,
又θ∈[0,2π),可得θ=.
3.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角α(0<α<π)的弧度数为
( )
A. B.
C. D.
解析:选C 设圆的半径为R,由题意可知,圆内接正三角形的边长为R,所以圆弧长为R,所以该圆弧所对圆心角的弧度数为=.
4.下列选项中正确的是( )
A.sin 300°>0 B.cos(-305°)<0
C.tan>0 D.sin 10<0
解析:选D 300°=360°-60°,则300°是第四象限角;
-305°=-360°+55°,则-305°是第一象限角;
因为-=-8π+,所以-是第二象限角;
因为3π<10<,所以10是第三象限角.故sin 300°<0,cos(-305°)>0,tan<0,sin 10<0,故D正确.
5.已知角α=2kπ-(k∈Z),若角θ与角α的终边相同,则y=++的值为( )
A.1 B.-1
C.3 D.-3
解析:选B 由α=2kπ-(k∈Z)及终边相同的概念知,角α的终边在第四象限,又角θ与角α的终边相同,所以角θ是第四象限角,所以sin θ<0,cos θ>0,tan θ<0.
所以y=-1+1-1=-1.
6.若α=1 560°,角θ与α终边相同,且-360°<θ<360°,则θ=________.
解析:因为α=1 560°=4×360°+120°,
所以与α终边相同的角为360°×k+120°,k∈Z,
令k=-1或k=0可得θ=-240°或θ=120°.
答案:120°或-240°
7.若两个圆心角相同的扇形的面积之比为1∶4,则这两个扇形的周长之比为________.
解析:设两个扇形的圆心角的弧度数为α,半径分别为r,R(其中r<R),则=,
所以r∶R=1∶2,两个扇形的周长之比为=1∶2.
答案:1∶2
8.点P从(-1,0)出发,沿单位圆顺时针方向运动 弧长到达点Q,则点Q的坐标为________.
解析:设点A(-1,0),点P从(-1,0)出发,沿单位圆顺时针方向运动 弧长到达点Q,则∠AOQ=-2π=(O为坐标原点),所以∠xOQ=,cos=,sin=,所以点Q的坐标为.
答案:
9.如图,在平面直角坐标系xOy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.
(1)若点B的横坐标为-,求tan α的值;
(2)若△AOB为等边三角形,写出与角α终边相同的角β的集合.
解:(1)设点B的纵坐标为m,则由题意m2+2=1,
且m>0,所以m=,故B,
根据三角函数的定义得tan α==-.
(2)若△AOB为等边三角形,则∠AOB=,故与角α终边相同的角β的集合为.
10.已知扇形AOB的周长为8.
(1)若这个扇形的面积为3,求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.
解:设扇形AOB的半径为r,弧长为l,圆心角为α,
(1)由题意可得
解得或
∴α==或α==6.
(2)法一:∵2r+l=8,
∴S扇=lr=l·2r≤2=×2=4,
当且仅当2r=l,即r=2,l=4,α==2时,扇形面积取得最大值4.
∴圆心角α=2,弦长AB=2sin 1×2=4sin 1.
法二:∵2r+l=8,
∴S扇=lr=r(8-2r)=r(4-r)=-(r-2)2+4≤4,
当且仅当r=2,l=4,即α==2时,扇形面积取得最大值4.
∴弦长AB=2sin 1×2=4sin 1.
B级——拔高题目稳做准做
1.已知点P落在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A. B.
C. D.
解析:选D 由sin >0,cos <0知角θ是第四象限角,
因为tan θ==-1,θ∈[0,2π),
所以θ=.故选D.
2.已知sin α>sin β,那么下列命题成立的是( )
A.若α,β是第一象限的角,则cos α>cos β
B.若α,β是第二象限的角,则tan α>tan β
C.若α,β是第三象限的角,则cos α>cos β
D.若α,β是第四象限的角,则tan α>tan β
解析:选D 由三角函数线可知选D.
3.若角α是第三象限角,则是第________象限角.
解析:因为2kπ+π<α<2kπ+(k∈Z),
所以kπ+<<kπ+(k∈Z).
当k=2n(n∈Z)时,2nπ+<<2nπ+,是第二象限角,
当k=2n+1(n∈Z)时,2nπ+<<2nπ+,是第四象限角,
综上知,当α是第三象限角时,是第二或四象限角.
答案:二或四
4.(2018·石家庄模拟)在(0,2π)内,使sin x>cos x成立的x的取值范围为_____________.
解析:如图所示,找出在(0,2π)内,使sin x=cos x的x值,sin=cos=,sin=cos=-.根据三角函数线的变化规律标出满足题中条件的角x∈.
答案:
5.已知角α的终边在直线y=-3x上,求10sin α+的值.
解:设α终边上任一点为P(k,-3k),
则r==|k|.
当k>0时,r=k,
∴sin α==-,==,
∴10sin α+=-3+3=0;
当k<0时,r=-k,∴sin α==,
==-,
∴10sin α+=3-3=0.
综上,10sin α+=0.
6.若角θ的终边过点P(-4a,3a)(a≠0),
(1)求sin θ+cos θ的值;
(2)试判断cos(sin θ)·sin(cos θ)的符号.
解:(1)因为角θ的终边过点P(-4a,3a)(a≠0),
所以x=-4a,y=3a,r=5|a|,
当a>0时,r=5a,sin θ+cos θ=-=-.
当a<0时,r=-5a,sin θ+cos θ=-+=.
(2)当a>0时,sin θ=∈,
cos θ=-∈,
则cos(sin θ)·sin(cos θ)
=cos ·sin<0;
当a<0时,sin θ=-∈,
cos θ=∈,
则cos(sin θ)·sin(cos θ)
=cos·sin >0.
综上,当a>0时,cos(sin θ)·sin(cos θ)的符号为负;
当a<0时,cos(sin θ)·sin(cos θ)的符号为正.