- 2021-05-20 发布 |
- 37.5 KB |
- 17页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学好题精选66道
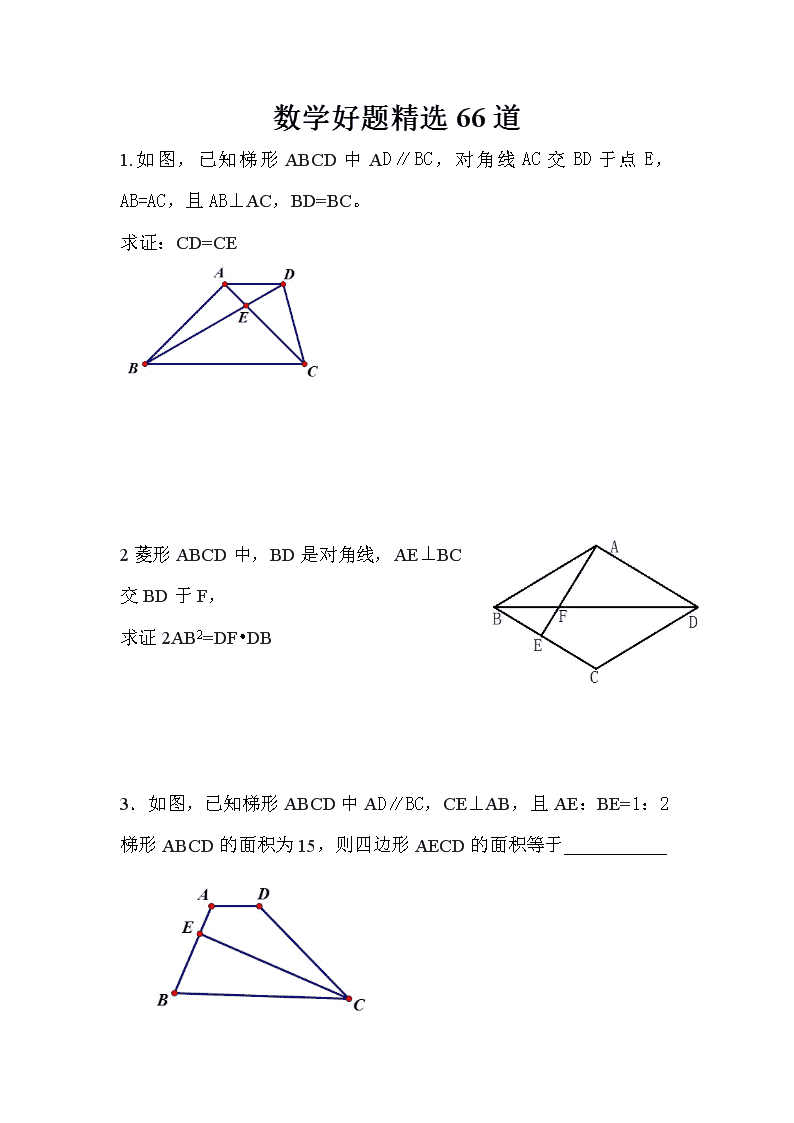
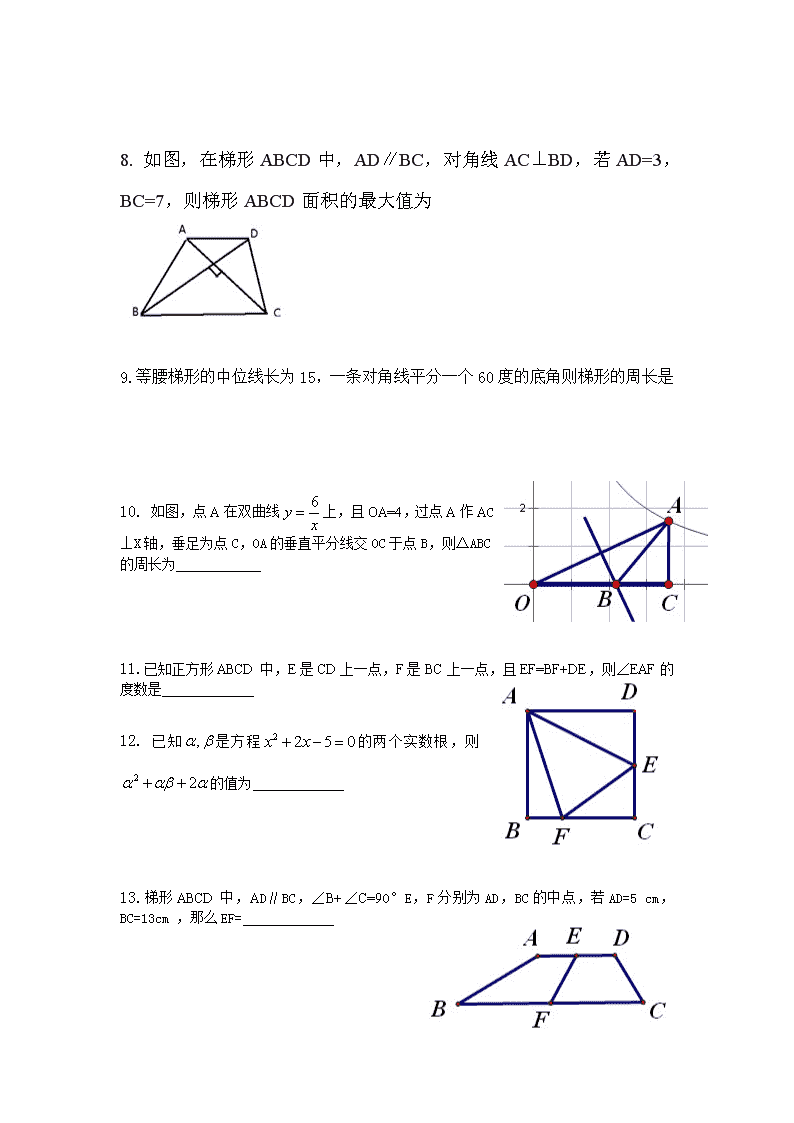
数学好题精选66道 1.如图,已知梯形ABCD中AD∥BC,对角线AC交BD于点E,AB=AC,且AB⊥AC,BD=BC。 求证:CD=CE 2菱形ABCD中,BD是对角线,AE⊥BC交BD于F, 求证2AB2=DF•DB 3.如图,已知梯形ABCD中AD∥BC,CE⊥AB,且AE:BE=1:2梯形ABCD的面积为15,则四边形AECD的面积等于 4.甲,乙两人在周长为400米的正方形水池相邻的两角上同时同向绕池边行走,乙在甲后。甲每分钟走50米,乙每分钟走44米。问:甲,乙两人自出发后初次在同一边上行走花了多少时间? 5.已知:x满足不等式3x+4≦6+2(x-2) 求的最小值 6 .关于x,y的二元一次方程组的解满足x-y>0求k的取值范围. 7. 如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数的图像交于A点和B点,若C为x轴上任意一点,连接AC,BC则△ABC的面积为 【 】 8. 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=3,BC=7,则梯形ABCD面积的最大值为 9.等腰梯形的中位线长为15,一条对角线平分一个60度的底角则梯形的周长是 10. 如图,点A在双曲线上,且OA=4,过点A作AC⊥X轴,垂足为点C,OA的垂直平分线交OC于点B,则△ABC的周长为 11.已知正方形ABCD中,E是CD上一点,F是BC上一点,且EF=BF+DE,则∠EAF的度数是 12. 已知是方程的两个实数根,则的值为 13.梯形ABCD中,AD∥BC,∠B+∠C=90°E,F分别为AD,BC的中点,若AD=5 cm, BC=13cm ,那么EF= 14. 如图,在□ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在边CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则FC的长为 15. 如图,在菱形ABCD中,对角线AC=16 cm,BD=12 cm,BE⊥DC于点E,则BE的长为 16.如图所示,在△ABC中,AB=AC,AD=AE, ∠EDC=20°,则∠DAB的度数为 . 17.已知△ABC的周长为24cm,M是AB的中点,MC=MA=5cm,则△ABC的面积= . 41..如图,一个等边三角形的边长和与它的一边相外切的 圆的周长相等,当这个圆按箭头方向从某一位置沿等边三 角形的三边做无滑动旋转,直至回到原出发位置时,则这个 圆共转了( ) A.4圈 B.3圈 C.5圈 D.3.5圈 18.有一张矩形纸片ABCD,其中AD=4cm,上面有一个以AD为直径的半园,正好与对边BC相切,如图(甲)。将它沿DE折叠,是A点落在BC上,如图(乙)。这时,半圆还露在外面的部分(阴影部分)的面积是( ) A B C D 第12题图甲 A、(π-)cm2 B、(π+)cm2 C、(π-)cm2 D、(π+)cm2 19.如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm。 2 0 4 http://www.1230.org6 8 20.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C, AC平分∠DAB. (1)求证:AD⊥DC (2)若AD=2,AC=,求AB的长. 21. 当一枚硬币不动,另一枚硬币绕它旋转一周时,则旋转的这枚硬币自己转了 圈? 22. . 如图,⊙O的直径AB为10 cm,弦AC为6 cm,∠ACB的平分线交AB于E,交⊙O于D.求弦AD、CD的长. 23. 如图6,在Rt△ABC中,∠ABC=90°,D是AC的中点, ⊙O经过A、B、D三点,CB的延长线交⊙O于点E. (1) 求证AE=CE; (2) EF与⊙O相切于点E,交AC的延长线于点F, 若CD=CF=2cm,求⊙O的直径; (3)若 (n>0),求sin∠CAB. 24. 如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD. (第5题图) (1)求证:∠ADB=∠E;(3分) (2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.(3分) (3)当AB=5,BC=6时,求⊙O的半径.(4分) 25. 已知:如图,中,,以为直径的⊙O交于点,于点. C P B O A D (第2题) (1)求证:是⊙O的切线; (2)若,求的值. 26. 如图△ABC内接于⊙O,过点B作⊙O的切线,交于CA的延长线于点E,∠EBC=2∠C. (1)求证:AB=AC;(2)当=时,①求tan∠ABE的值;②如果AE=,求AC的值。 27.关于x的一元二次方程x2-x+p-1=0有两个实数根x1,x2, (1)求p的取值范围. (2)若[2+ x1(1- x2,)] [2+ x2(1- x1,)]=9,求p的值.(利用韦达定理) (3)若[2+ x1(1- x1,)] [2+ x2(1- x2,)]=9,求p的值. (利用方程根的意义) 28. 如图,点E为矩形ABCD的AD边上的一点,EF⊥AC,EG⊥BD,且AB=6,BC=8,求EF+EG的值. 29. 如图,点E为边长为1的正方形ABCD的对角线BD边上的一点,且BE=BC,点P为EC上任意一点PM⊥BD,PN⊥BC, 求PM+PN的值. 30. 如图,在梯形ABCD中,DC∥AB,∠A+∠B=90°若AB=10,AD=4,DC=5, 则梯形ABCD的面积为 31. 15、已知A(x1,y2),B(x2,y2)都在图像上。若x1 x2=-3则y1 y2的值为 32. 若一个菱形的边长为2,则这个菱形两条对角线的平方和为 ( ) A、16 B、8 C、4 D、1 33. 菱形对角线的平方和等于一边平方的( ) A、8倍 B、6倍 C、4倍 D、2倍 34. 如图,在梯形ABCD中,DC∥AB,∠A+∠B=90°若AB=10, DC=4,点E、F分别为CD、AB中点, 则EF的长为 35如图,四边形ABCD是正方形,点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于F. (1) 求证:DE-BF=EF. (2) 当点G为BC的中点时,试探索线段EF与GF之间的数量关系,并说明理由 36.如图,□ABCD中,F为BC边上的一点,AF交BD与E,且BF:FC=2:3,若则四边形EFCD的面积为 37.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连接ED,FD,要使四边形AEDF为平行四边形,需要添加条件 38.如图,□ABCD中,分别以AD、BC,为边向内作等边△ADE和等边△BCF,连接BE、DF。求证:四边形BEDF是平行四边形。 39.如图,将矩形ABCD的顶点A与C重合后折叠,得折痕EF,若AB=6,BC=8。求折痕EF的长。 N E B C D A H 40.如图,在直角梯形ABCD中,AD//BC,ÐABC=90°,BD ^DC,BD=DC,CE平分ÐBCD,交AB于点E,交BD于 点H,EN//DC交BD于点N。下列结论: j BH=DH;k CH=(+1)EH;l =; 其中正确的是 (A) jkl (B) 只有kl (C) 只有k (D) 只有l 。 41. 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________. A E B C D F G H 42. 已知:如图,在梯形ABCD中,AD//BC,AB=DC=AD=2, BC=4。求ÐB的度数及AC的长。 A B C D 43. 如图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H. (1)证明:△ABG≌△ADE; (2)试猜想∠BHD的度数,并说明理由; (3)将图中正方形ABCD绕点A逆时针旋转(0°<∠BAE<180°),设△ABE的面积为S1,△ADG的面积为S2,判断S1与S2的大小关系,并给予证明. 44. 如图,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( ) A D B C E F (第10题) A.12 cm2 B.18 cm2 C.24 cm2 D.30 cm2 45.如图所示,在折纸活动中,小明制作了一张纸片,点分别是边、上,将沿着折叠压平,与重合,若,则( ) A. B. C. D. 46.如图,两同心圆的圆心为,大圆的弦切小圆于,两圆的半径分别为 和,则弦长= ;若用阴影部分围成一个圆锥,则该圆锥的底面半径 为 .(结果保留根号) N E B C D A H 47如图,在直角梯形ABCD中,AD//BC,ÐABC=90°,BD ^DC,BD=DC,CE平分ÐBCD,交AB于点E,交BD于 点H,EN//DC交BD于点N。下列结论: j BH=DH;k CH=(+1)EH;l =; 其中正确的是 (A) jkl (B) 只有kl (C) 只有k (D) 只有l 。 y A B C x O 48.如图,直线y= -x+b与y轴交于点A,与双曲线y=在第一象 限交于B、C两点,且AB·AC=4,则k= 。 A B C O E P 49. (本题满分8分) 如图,点O在ÐAPB的平分在线,圆O与PA相切于 点C; (1) 求证:直线PB与圆O相切; (2) PO的延长线与圆O交于点E。若圆O的半径为3,PC=4。 求弦CE的长。 50. . 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________. 51. 、是一次函数图象上不同的两点,若,则( ). A. B. C. D. (第58题) 52. 如图,将△ABC绕点C(0,-1)旋转180°得到△ABC,设点A的坐标为则点A’的坐标为【 】 (A) (B) (C) (D) A B C D E F 53. 在锐角△ABC中,∠BAC=60º,BD、CE为高,F为BC的中点, 连接DE、DF、EF,则结论:①DF=EF;②AD∶AB=AE∶AC; ③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45º时, BE=DE中,一定正确的有( ) A.2个 B.3个 C.4个 D.5个 第(60)题 D C A F B E G 54. 如图,等边三角形中,、分别为、边上 的点,,与交于点,于点, 则的值为 . 55.已知,点A的坐标为(a,0)点B的坐标为(a+3,0)点C的坐标为(4,-1)点D的坐标为(-2,-4),求a的值为多少时,四边形ABCD的周长最小? 56. 已知,如图,菱形ABCD的边长为10,对角线AC=16, G 为 AB中点,E、F为对角线AC上的两点,且EF=2,求四边形BFEG的周长的最小值。 57.(2009陕西)(本题满分8分) 如图,⊙O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P. (1)求证:AP是⊙O的切线; (2)若⊙O的半径R=5,BC=8,求线段AP的长. 58.(2009陕西)(本题满分10分) 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2). (1)求点B的坐标; (2)求过点A、O、B的抛物线的表达式; (3)连接AB,在(2)中的抛物线上求出点P,使得S△ABP=S△ABO. 59.(2010陕西)如图,在RT△ABC中∠ABC=90°,斜边AC的垂直平分线交BC与D点,交AC与E点,连接BE (1)若BE是△DEC的外接圆的切线,求∠C的大小? (2)当AB=1,BC=2时求△DEC外接圆的半径 60.(2010陕西)如图,在平面直角坐标系中,抛物线A(-1,0),B(3,0)C(0,-1)三点。 (1)求该抛物线的表达式; (2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形求所有满足条件点P的坐标。 61.(2011陕西)(本题满分8分) 如图,在△ABC中,,⊙O是△ABC外接圆,过点A 作的切线,交CO的延长线于P点,CP交⊙O于D (1) 求证:AP=AC (2) 若AC=3,求PC的长 62.(2011陕西)(本题满分10分) 如图,二次函数的图像经过△AOC的三个顶点,其中A(-1,m),B(n,n) (1) 求A、B的坐标 (2) 在坐标平面上找点C,使以A、O、B、C为顶点的四边形是平行四边形 ①、 这样的点C有几个? ②、 能否将抛物线平移后经过A、C两点,若能求出平移后经过A、C两点的一条抛物线的解析式;若不能,说明理由。 63.已知:梯形ABCD中,点Q、P分别为BC、AD边上的动点,PE∥AQ,PF∥DQ,S梯形ABCD=7,AD=3,BC=4求S△PEF的最大值 64.如图,在△ABC,,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且。 (1)求证:直线BF是⊙O的切线; (2)若,,求BC和BF的长。 65.在平面直角坐标系xOy中,二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。 (1)求点A的坐标; (2)当时,求m的值; (3)已知一次函数,点P(n,0)是x轴上的一个动点,在(2)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数的图象于N。若只有当时,点M位于点N的上方,求这个一次函数的解析式。 66.在右表中,我们把第i行第j列的数记为(其中i,j都是不大于5的正整数),对于表中的每个数,规定如下:当时,;当时,。例如:当,时,。按此规定,_____;表中的25个数中,共有_____个1;计算 的值为________。查看更多