- 2021-05-20 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
苏科版八年级数学上册有关等腰三角形的性质和判定应用的常见类型(含答案)
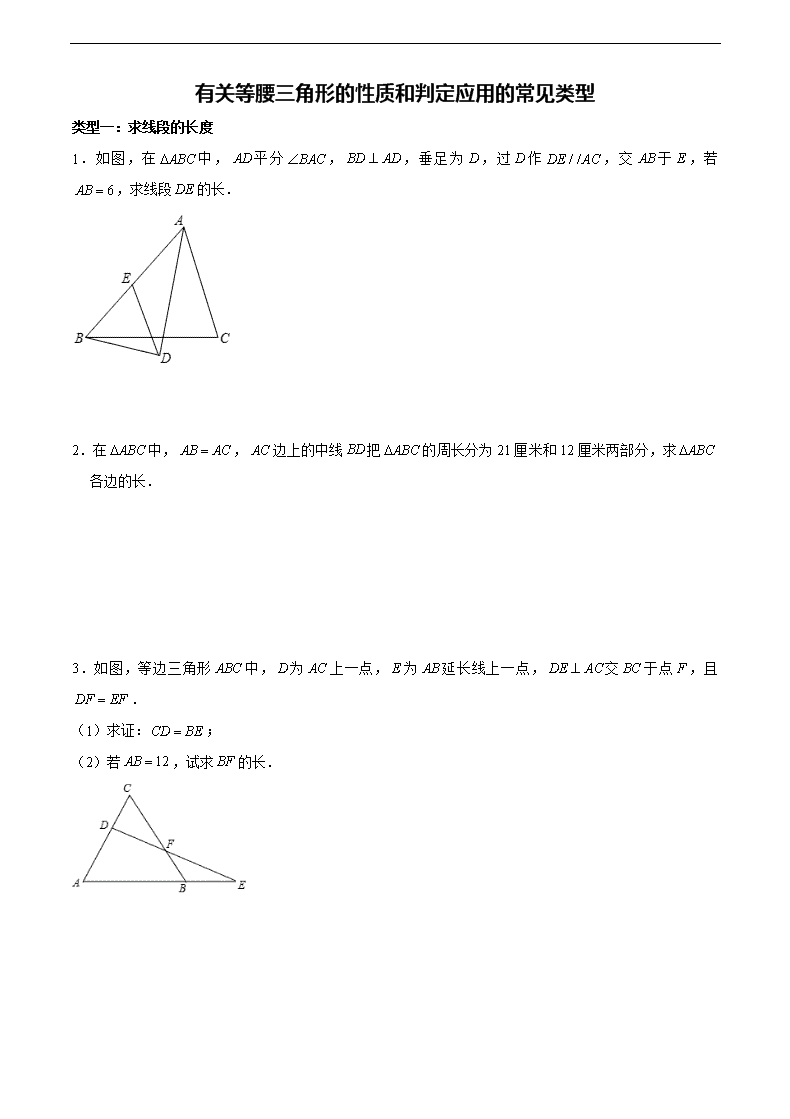
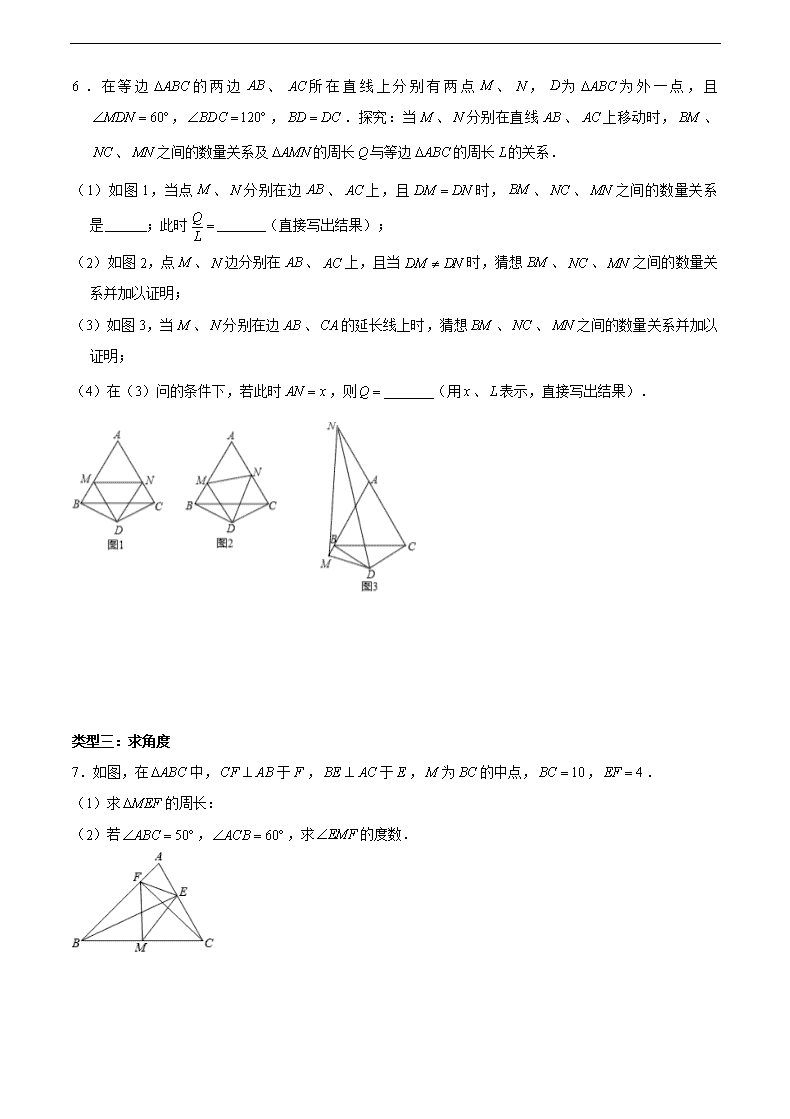
有关等腰三角形的性质和判定应用的常见类型 类型一:求线段的长度 1.如图,在 ABC 中,AD 平分 BAC ,BD AD ,垂足为 D ,过 D 作 / /DE AC ,交 AB 于 E ,若 6AB , 求线段 DE 的长. 2.在 ABC 中,AB AC ,AC 边上的中线 BD 把 ABC 的周长分为 21 厘米和 12 厘米两部分,求 ABC 各 边的长. 3.如图,等边三角形 ABC 中, D 为 AC 上一点, E 为 AB 延长线上一点, DE AC 交 BC 于点 F ,且 DF EF . (1)求证: CD BE ; (2)若 12AB ,试求 BF 的长. 类型二:证明线段之间的关系 4.已知:如图,在 ABC 中,AB AC , 120A ,AB 的垂直平分线 MN 分别交 BC ,AB 于点 M ,N , 求证: 2CM BM . 5.【阅读理解】 截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相 等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题. (1)如图 1, ABC 是等边三角形,点 D 是边 BC 下方一点, 120BDC ,探索线段 DA 、 DB 、 DC 之 间的数量关系. 解题思路:延长 DC 到点 E ,使CE BD ,连接 AE ,根据 180BAC BDC ,可证 ABD ACE 易 证得 ABD ACE ,得出 ADE 是等边三角形,所以 AD DE ,从而探寻线段 DA 、 DB 、 DC 之间的 数量关系. 根据上述解题思路,请直接写出 DA 、 DB 、 DC 之间的数量关系是 ; 6.在等边 ABC 的两边 AB 、AC 所在直线上分别有两点 M 、N ,D 为 ABC 为外一点,且 60MDN , 120BDC , BD DC .探究:当 M 、 N 分别在直线 AB 、 AC 上移动时, BM 、 NC 、 MN 之间的 数量关系及 AMN 的周长 Q 与等边 ABC 的周长 L 的关系. (1)如图 1,当点 M 、 N 分别在边 AB 、 AC 上,且 DM DN 时, BM 、 NC 、 MN 之间的数量关系 是 ;此时 Q L (直接写出结果); (2)如图 2,点 M 、 N 边分别在 AB 、 AC 上,且当 DM DN 时,猜想 BM 、 NC 、 MN 之间的数量关 系并加以证明; (3)如图 3,当 M 、 N 分别在边 AB 、 CA 的延长线上时,猜想 BM 、 NC 、 MN 之间的数量关系并加以 证明; (4)在(3)问的条件下,若此时 AN x ,则 Q (用 x 、 L 表示,直接写出结果). 类型三:求角度 7.如图,在 ABC 中, CF AB 于 F , BE AC 于 E , M 为 BC 的中点, 10BC , 4EF . (1)求 MEF 的周长: (2)若 50ABC , 60ACB ,求 EMF 的度数. 类型四:证明角度之间的关系 8.已知 ABC ,AB AC ,D 为直线 BC 上一点,E 为直线 AC 上一点,AD AE ,设 BAD , CDE . (1)如图,若点 D 在线段 BC 上,点 E 在线段 AC 上. ①如果 60ABC , 70ADE ,那么 , . ②求 , 之间的关系式. (2)是否存在不同于以上②中的 , 之间的关系式?若存在,求出这个关系式(求出一个即可);若不 存在,说明理由. 9.如图, ABC 中, ABC ACB ,点 D 在 BC 所在的直线上,点 E 在射线 AC 上,且 AD AE ,连接 DE . (1)如图①,若 35B C , 80BAD ,求 CDE 的度数; (2)如图②,若 75ABC ACB , 18CDE ,求 BAD 的度数; (3)当点 D 在直线 BC 上(不与点 B 、 C 重合)运动时,试探究 BAD 与 CDE 的数量关系,并说明理 由. 有关等腰三角形的性质和判定应用的常见类型 参考答案与试题解析 类型一:求线段的长度 1.解: AD 平分 BAC , / /DE AC , EAD CAD , EDA CAD , EAD EDA , BD AD , EBD EAD BDE EDA EBD BDE , DE BE , 1 1 6 32 2DE AB . 【点评】该题主要考查了等腰三角形的判定与性质、直角三角形的性质、平行线的性质等几何知识点的应 用问题;灵活运用有关定理来分析、判断是解题的关键. 2.解:如图, 设 2AB AC , BC ; BD 是中线, AD CD ; 若 21AB AD , 12BC CD ,即 2 21 12 , 解得: 7 , 5 ,此时, 14AB AC , 5BC ; 若 12AB AD , 21BC CD ,即 2 12 21 , 解得: 4 , 17 , 此时 8AB AC , 17BC , AB AC BC , 4 , 17 ,不合题意,舍去. 综上所述, ABC 各边的长为14cm 、14cm 、 5cm . 【点评】该题以等腰三角形为载体,以三角形三边关系的考查为核心构造而成;解题的关键是运用分类讨 论的数学思想,列出方程逐一解析,问题即可解决. 3.解:(1)如图,作 / /DM AB ,交 CF 于 M ,则 MDF E , ABC 是等边三角形, 60C CDM CMD , CDM 是等边三角形, CD DM , 在 DMF 和 EBF 中, MDF E DF EF DFM EFB , ( )DMF EBF ASA , DM BE , CD BE ; (2) ED AC , 60A ABC , 30E BFE DFM FDM , BE BF , DM FM , 又 DMF EBF , MF BF , CM MF BF , 又 12AB BC , 4CM MF BF . 【点评】本题主要考查了等边三角形的性质、全等三角形的判定与性质的综合应用,解决问题的关键是作 平行线,构造等边三角形和全等三角形,根据全等三角形的性质以及等边三角形的性质进行求解. 类型二:证明线段之间的关系 4.证法 1:如答图所示,连接 AM , 120BAC , AB AC , 30B C , MN 是 AB 的垂直平分线, BM AM , 30BAM B , 90MAC , 2CM AM , 2CM BM . 证法二:如答图所示,过 A 作 / /AD MN 交 BC 于点 D . MN 是 AB 的垂直平分线, N 是 AB 的中点. / /AD MN , M 是 BD 的中点,即 BM MD . AC AB , 120BAC , 30B C , 90BAD BNM , 1 2AD BD BM MD , 又 120 90 30CAD BAC BAD , CAD C , AD DC , BM MD DC , 2CM BM . 【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点 的距离相等. 5.解:(1)如图 1,延长 DC 到点 E ,使 CE BD ,连接 AE , ABC 是等边三角形, AB AC , 60BAC , 120BDC , 180ABD ACD , 又 180ACE ACD , ABD ACE , ( )ABD ACE SAS , AD AE , BAD CAE , 60ABC ,即 60BAD DAC , 60DAC CAE ,即 60DAE , ADE 是等边三角形, DA DE DC CE DC DB ,即 DA DC DB , 故答案为: DA DC DB ; 【点评】此题是三角形的综合题,主要考查了考查的是全等三角形的判定和性质、直角三角形的性质、等 边三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键. 6.解:(1)如图 1,猜想: MN BM NC ,理由是: DM DN , 60MDN , MDN 是等边三角形, MN DM DN , 120BDC , BD DC , 30DBC DCB , ABC 是等边三角形, 60ABC ACB , 90DBM DCN , BD CD , DM DN , Rt DBM Rt DCN , 30BDM CDN , BM CN , 2DM BM , 2DM MN BM BM NC , AB AC , BM CN , AM AN , 60A , AMN 是等边三角形, AMN 的周长 3 6Q MN BM , 等边△ 4BC 的周长 3 3( ) 9L AB AM BM BM , 6 2 9 3 Q BM L BM , 故答案为: MN BM NC , 2 3 ; (2) MN BM CN , 如图 2,延长 AC 到 E ,使 CE BM ,连接 DE , ABC 是等边三角形, 60ABC ACB , BD CD , 120BDC , 30DBC DCB , ABC DBC ACB DCB , 即 90ABD ACD , 180 180 90 90DCE ACD , 在 Rt DBM 和 Rt DCE 中, 90 BD CD ABD DCE BM CE , ( )DBM DCE HL , DM DE , BDM CDE , 120BDC , 60MDN , 120 60 60BDM CDN , 即 60CDE CDN , 60NDE , 在 MDN 和 EDN 中, 60 DM DE MDN EDN DN DN , ( )MDN EDN SAS , MN NE , NE CN CE , CE BM , MN BM CN ; (3) CN BM MN ;在 NC 上截取CF BM ,连接 DF , 由(2)知: 90ABD ACD , 180 90 90MBD , 在 DBM 和 DCF 中, BD CD DBM DCF BM CF , ( )DBM DCF SAS , BDM CDF , DM DF , 60MDN BDM BDN CDF BDN 120BDC , 60NDF , 在 MDN 和 FDN 中, 60 MD FD MDN FDN DN DN , ( )MDN FDN SAS , MN NF , CN NF CF ,CF BM , CN MN BM ; (4)如图 3,等边 ABC 的周长为 L , 3 LAB , AMN 的周长 Q MN AN AM FN AN AB BM AN AF AN AB CF 2 2x AB , 22 3x L ,故答案为: 22 3x L . 【点评】此题是三角形的综合题,考查了等边三角形,直角三角形,等腰三角形的性质以及全等三角形的 判定与性质等知识.此题综合性很强,难度适中,解题的关键是注意数形结合思想的应用与辅助线的作 法. 类型三:求角度 7.解:(1) CF AB , BE AC , M 为 BC 的中点, 1 52EM BC , 1 52FM BC , MEF 周长 4 5 5 14EF EM FM ; (2) BM FM , 50ABC , 50MBF MFB , 180 2 50 80BMF , CM EM , 60ACB , 60MCE MEC , 180 2 60 60CME , 180 40EMF BMF CME . 【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,平 角的定义,是基础题,熟记性质并准确识图是解题的关键. 类型四:证明角度之间的关系 8.解:(1)① AB AC , 60ABC , 60BAC , AD AE , 70ADE , 180 2 40DAE ADE , 60 40 20BAD , 60 20 80ADC BAD ABD , 10CDE ADC ADE , 故答案为:20,10; ②设 ABC x , AED y , ACB x , AED y , 在 DEC 中, y x ,在 ABD 中, x y x , 2 ; (2)①当点 E 在 CA 的延长线上,点 D 在线段 BC 上, 如图 1:设 ABC x , ADE y , ACB x , ACE y , 在 ABD 中, x y ,在 DEC 中, 180x y , 2 180 , ②当点 E 在 CA 的延长线上,点 D 在 CB 的延长线上, 如图 2,同①的方法可得 180 2 . 【点评】此题是三角形综合题,主要考查了等腰三角形的性质,三角形的内角和定理,解本题的关键是利 用三角形的内角和定理得出等式. 9.解:(1) 35B C , 110BAC , 80BAD , 30DAE , 75ADE AED , 180 35 30 75 40CDE ; (2) 75ACB , 18CDE , 75 18 57E , 57ADE AED , 39ADC , 75ABC ADB DAB , 36BAD ; (3)设 ABC ACB y , ADE AED x , CDE , BAD ①如图 1,当点 D 在点 B 的左侧时, ADC x , (1) (2) y x y x , (1) (2)得 2 0 , 2 ; ②如图 2,当点 D 在线段 BC 上时, ADC x , (1) (2) x y x y , (2) (1)得 , 2 ; ③如图 3,当点 D 在点 C 右侧时, ADC x , 180 (1) 180 (2) x y y x , (2) (1)得 2 0 , 2 . 综上所述, BAD 与 CDE 的数量关系是 2 CDE BAD . 【点评】本题考查了等腰三角形的性质,三角形的外角的性质,三角形的内角和,正确的识别图形是解题 的关键.查看更多