2019届二轮复习圆与圆的位置关系课件(33张)(全国通用)(全国通用)
圆与圆的位置关系
d
d
d
r
r
r
几何法
位置关系
相交
相切
相离
d
r
代数法
交点个数
△=0
△>0
△<0
2
1
0
图形
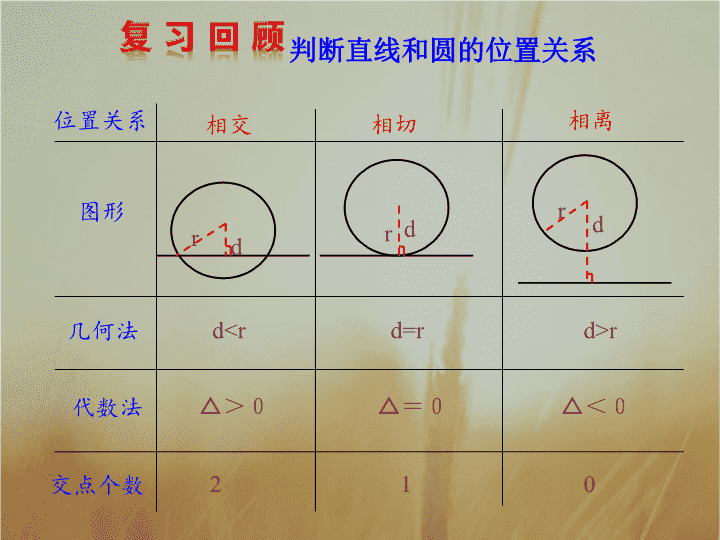
判断直线和圆的位置关系
圆与圆有哪几种位置关系呢?
你能从生活中举几个圆和圆的位置关系的例子吗?
思考
下面我们就进入今天的学习内容,圆与圆的位置关系!
总结
1.
理解圆与圆的位置关系的种类
.
2.
会根据两圆的圆心距与半径之间的关系判断出
两圆的位置关系
.
(重点、难点)
3.
会求两相交圆的公共弦方程、公切线方程
.
探究
圆与圆的位置关系
1.
相离(没有公共点)
2.
相切(一个公共点)
3.
相交(两个公共点)
外离
内含(同心圆)
内切
外切
外离
圆和圆的五种位置关系
d>R+r
d=R+r
R-rd≥0.
2.
利用代数方法判断
(
1
)当
Δ=0
时,有一个交点,两圆内切或外切,
(
2
)当
Δ<0
时,没有交点,两圆内含或相离,
消去其中的一个未知数
y
或
x
,得关于
x
或
y
的一元二次方程
.
将两个圆方程联立
,
得
(
3
)当
Δ>0
时,有两个交点,两圆相交
.
两种方法的优缺点;
几何方法直观,但不能求出交点;
代数方法能求出交点,但
Δ=0
,
Δ<0
时,不能准确判断圆的位置关系
.
例
1
:
已知圆
圆
试判断圆
C
1
与圆
C
2
的位置关系
.
【
提升总结
】
方法二,代数法.
由两者方程组成方程组,由方程组解的情况决定
.
解法一:
把圆的方程都化成标准形式
,
为
的圆心坐标是
,
半径长
的圆心坐标是
,
半径长
分析:
方法一,几何法.
判断圆心距与两圆半径的和与差的绝对值的大小关系
.
所以圆心距
两圆半径的和与差
而
即
所以两圆相交
.
解法二:
将两个圆方程联立
,
得方程组
把上式代入①,并整理得
故两圆相交.
方程④根的判别式
所以方程④有两个不等实数根,方程组有两解;
圆
x
2
+y
2
-2x=0
与
x
2
+y
2
+4y=0
的位置关系是
( )
A.
相离
B.
外切
C.
相交
D.
内切
【
解析
】
选
C.
圆的方程分别化为
(x-1)
2
+y
2
=1,x
2
+(y+2)
2
=4,
因为两圆圆心距
d=
而两圆的半径和
r
1
+r
2
=3,
半径差
r
2
-r
1
=1
,
所以
r
2
-r
1
<
d
<
r
1
+r
2
,
所以两圆相交
.
【
变式练习
】
探究:
圆
与圆
相交于
A,B
两点,如何求公共弦的方程?
方法一:
将两圆方程联立,求出两个交点的坐标,利用两点式求公共弦的方程
.
方法二:
先来探究一般情形.
已知圆
与圆
相交于
A,B
两点,
设
那么
同理可得
由③④可知
一定在直线
显然通过两点的直线只有一条,即直线方程唯一,
故公共弦的方程为
消去二次项
所以前面探究问题可通过
(
D
1
-
D
2
)x+(E
1
-
E
2
)y+F
1
-
F
2
=0
得出
,
即公共弦的方程为:
2x+1=0
例
2:
已知圆
C
1
:
x
2
+y
2
-
10x
-
10y=0
和圆
C
2
:
x
2
+y
2
+6x+2y
-
40=0
相交于
A
、
B
两点,求公共弦
AB
的长
.
解法一:
由两圆的方程相减,消去二次项得到
一个二元一次方程,此方程为
4x+3y=10.
即为公共弦
AB
所在的直线方程,
由
解得
或
所以两点的坐标是
A(
-
2,6)
,
B(4,
-
2)
,或
A
(
4
,
-2
),
B
(
-2,6
),
故
|AB|=
圆
C
1
的圆心
C
1
(5
,
5 )
,半径
r
1
=
,
则
|C
1
D|=
所以
|AB|=2|AD|=
解法二:
先求出公共弦所在直线的方程:
4x+3y=10.
过圆
C
1
的圆心
C
1
作
C
1
D⊥AB
于
D.
两圆
O
1
:
x
2
+y
2
-6x+16y-48=0
与
O
2
:
x
2
+y
2
+4x-8y-44
=0
,其半径分别为
m
1
,m
2
,
则它们的公切线条数为
( )
A.1 B.2 C.3 D.4
【
变式练习
】
B
【
解析
】
选
B.
将两圆方程化为标准方程为
(x-3)
2
+(y+8)
2
=121,(x+2)
2
+(y-4)
2
=64.
所以
O
1
(3,-8),r
1
=11;O
2
(-2,4),r
2
=8.
因为
|O
1
O
2
|=
所以
3
<
|O
1
O
2
|
<
19,
所以两圆相交,从而公切线有两条
.
B
2.
若圆 相交,求实数
m
的范围
.
13+2
两圆心坐标及半径
r
1
,r
2
(配方法)
圆心距
d
(两点间距离公式)
比较
d
和
r
1
,
r
2
的和与差的大小,下结论
消去
y
几何方法
代数方法