- 2021-05-20 发布 |
- 37.5 KB |
- 20页


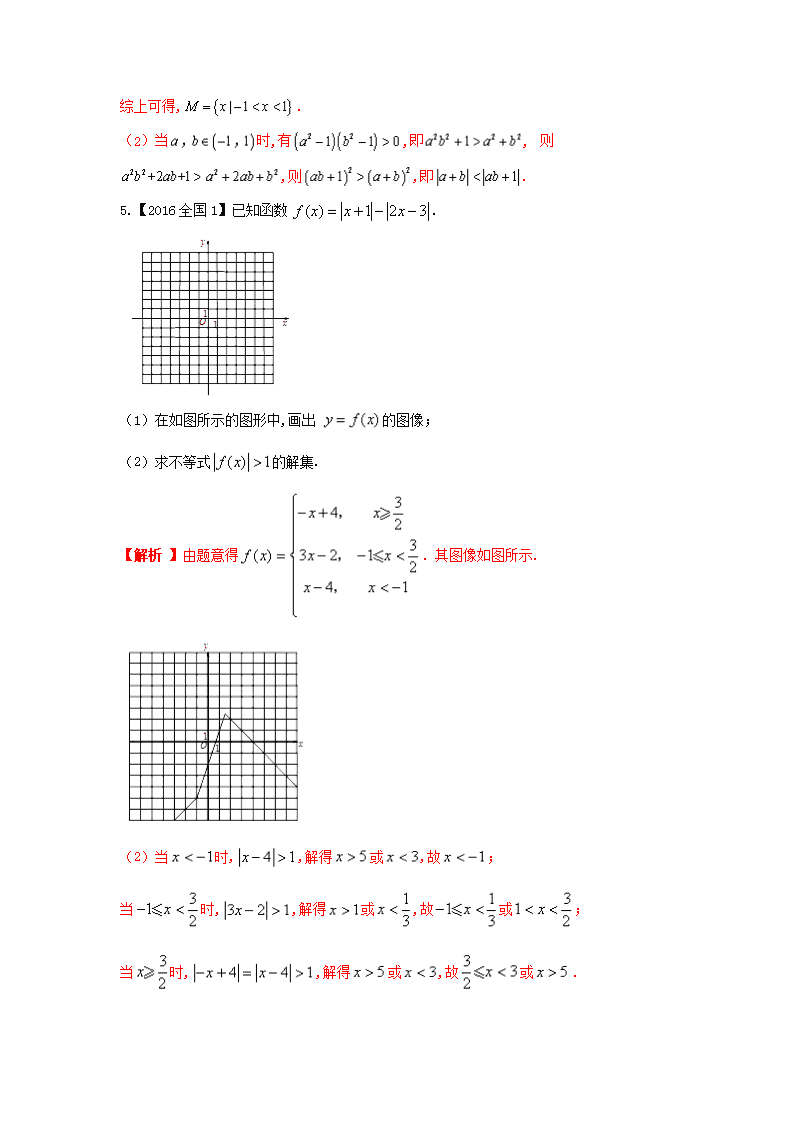
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教B版绝对值不等式和不等式的证明学案
热点二十四 绝对值不等式和不等式的证明(选修4-5) 【名师精讲指南篇】 【高考真题再现】 1.【2014全国卷1】若,且. (Ⅰ)求的最小值; (Ⅱ)是否存在,使得?并说明理由. 2.【2015全国卷1】已知函数,. (1)当时,求不等式的解集; (2)若的图像与x轴围成的三角形面积大于6,求的取值范围. 【解析】(1)当时,,即. 当时,,无解; 当时,,解得; 当时,,解得. 综上所述,当时,的解集为. (2),,作图,图像与轴所围成三角形的三个顶点为,,,,即,解得,所以的取值范围是. 3.【2015全国卷】设,,,均为正数,且.证明: (1)若,则; (2)是的充要条件. 【解析】(1)因为,,由题设,,得,因此. (2)( i)若,则,即.因为,所以,由(Ⅰ)得. ( ii)若,则, 即.因为,所以, 于是,因此. 综上,是的充要条件. 4.【2016全国卷2】已知函数,为不等式的解集. (1)求; (2)证明:当时,. 【解析】(1)当时,,所以; 当时,恒成立; 当时,,所以. 综上可得,. (2)当时,有,即, 则,则,即. 5.【2016全国1】已知函数. (1)在如图所示的图形中,画出的图像; (2)求不等式的解集. 【解析 】由题意得.其图像如图所示. (2)当时,,解得或,故; 当时,,解得或,故或; 当时,,解得或,故或. 综上所述,该不等式的解集为. 6.【2016全国3】已知函数 (1)当时,求不等式的解集; (2)设函数当时,,求的取值范围. 【热点深度剖析】 2014年高考本题考查基本不等式的灵活应用.2015年全国卷1考查绝对值不等式的解法,全国卷2考查不等式的证明及充要条件;2016年3套试卷都考查了绝对值不等式的解法,又分别考查了不等式的证明、绝对值函数的图象及恒成立问题. 从三年试题来看,高考对这部分要求不是太高,会解绝对值不等式,会利用柯西不等式,基本不等式求最值,而解绝对值不等式是高考的热点,预测2017年高考全国卷1可能会考不等式的证明,全国卷2,3可能会考绝对值不等式的解法,另外柯西不等式全国卷还没有考查过,应引起重视. 【重点知识整合】 1、含绝对值不等式的解法 ①|ax+b|≤c(c>0)⇔-c≤ax+b≤c, |ax+b|≥c(c>0)⇔ax+b≥c或ax+b≤-c, ②|x-a|+|x-b|≤c,|x-a|+|x-b|≥c型不等式的解法. 解法1:S1 令每个绝对值符号里的一次式为0,求出相应的根. S2 把这些根由小到大排序,它们把实数轴分成若干个小区间. S3 在所分区间上,根据绝对值的定义去掉绝对值符号,讨论所得的不等式在这个区间上的解集. S4 这些解集的并集就是原不等式的解集. 解法2:构造函数f(x)=|x-a|+|x-b|-c,写出f(x)的分段解析式作出图象,找出使f(x)≤0(或f(x)≥0)的x的取值范围即可. 解法3:利用绝对值的几何意义求解,|x-a|+|x-b|表示数轴上点P(x)到点A(a)、B(b)距离的和.关键找出到A、B两点距离之和为c的点,“≤”取中间,“≥”取两边. 注意这里c≥|a-b|,若c<|a-b|,则|x-a|+|x-b|≤c的解集为,|x-a|+|x-b|≥c的解集为R. 2、几个重要的不等式 (1)定理1 a2+b2≥2ab(a,b∈R),当且仅当a=b时取等号. 定理2 ≥(a,b∈R+),当且仅当a=b时取等号. 定理3 ≥(a,b,c∈R+),当且仅当a=b=c时,取等号. 定理4 (a1+a2+…+an)≥(ai∈R+,i=1,2,…,n),仅当a1=a2=…=an时取等号. (2)绝对值三角不等式 ①定理1 |a|+|b|≥|a+b|(a,b∈R),仅当ab≥0时等号成立. ②定理2 设a、b、c∈R,则|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立. ③推论 ||a|-|b||≤|a±b|≤|a|+|b|. (3)分式不等式 若a>b>n>0,m>0,则<<. 3、不等式的证明方法 (1)比较法:依据a>b⇔a-b>0,a查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档