西藏山南市第二高级中学2018-2019学年高一下学期期末考试数学试题

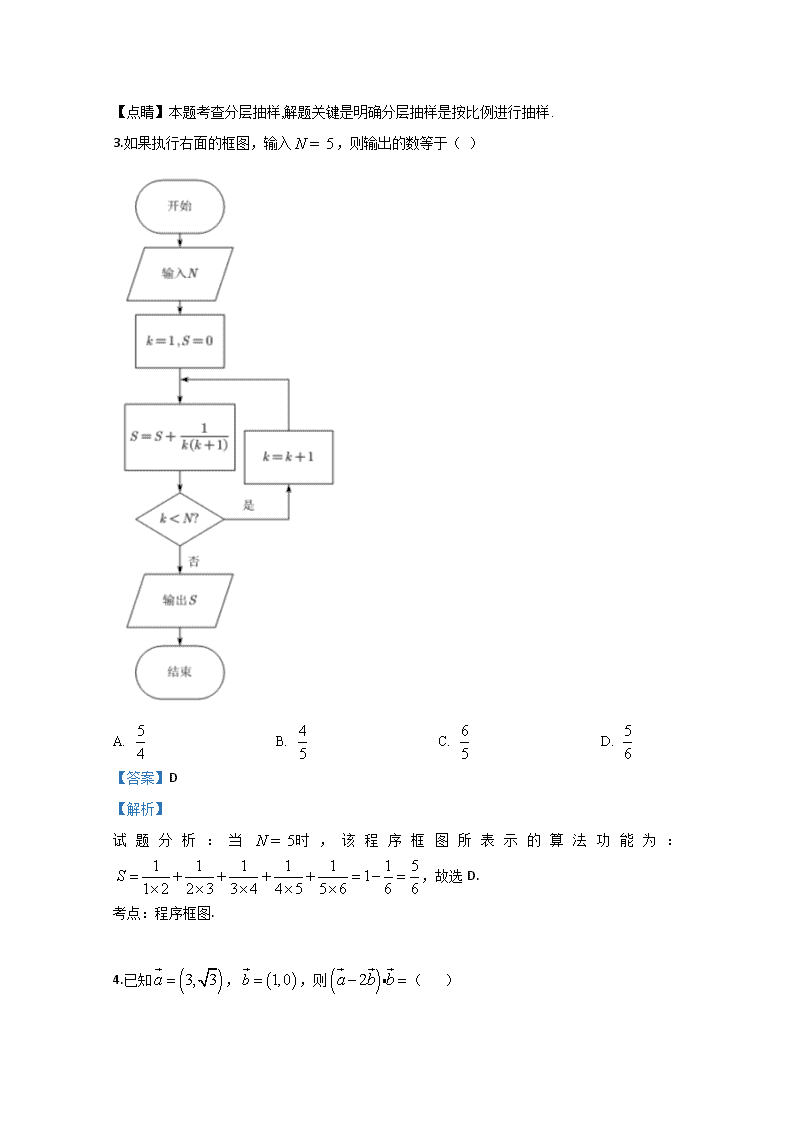
西藏山南市第二高级中学2018-2019学年高一下学期期末考试数学试题

‎2019年山南期末二高高一数学试卷 一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.如果角的终边经过点，那么的值是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据任意角的三角函数定义直接求解.‎ ‎【详解】因为角终边经过点,‎ 所以,‎ 故选:D.‎ ‎【点睛】本题考查任意角的三角函数求值,属于基础题.‎ ‎2.某市电视台为调查节目收视率，想从全市3个县按人口数用分层抽样的方法抽取一个容量为的样本，已知3个县人口数之比为，如果人口最多的一个县抽出60人，那么这个样本的容量等于（ ）‎ A. 96 B. ‎120 ‎C. 180 D. 240‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据分层抽样的性质,直接列式求解即可.‎ ‎【详解】因为3个县人口数之比为,而人口最多的一个县抽出60人,‎ 则根据分层抽样的性质,有,‎ 故选:B.‎ ‎【点睛】本题考查分层抽样,解题关键是明确分层抽样是按比例进行抽样.‎ ‎3.如果执行右面的框图，输入，则输出的数等于（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 试题分析：当时，该程序框图所表示的算法功能为：，故选D.‎ 考点：程序框图.‎ ‎4.已知，，则（ ）‎ A. 1 B. ‎2 ‎C. D. 3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据向量坐标运算法则直接求解.‎ ‎【详解】因为,,‎ 所以,‎ 所以,‎ 故选:A.‎ ‎【点睛】本题考查向量的坐标运算,属于基础题.‎ ‎5.掷两颗均匀的骰子，则点数之和为5的概率等于（　　）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【详解】试题分析：掷两颗均匀的骰子，共有36种基本事件，点数之和为5的事件有（1,4），（2,3），（3,2），（4,1）这四种，因此所求概率为，选B．‎ 考点：概率问题 ‎6.已知，则角的终边所在的象限为（ ）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎【答案】D ‎【解析】‎ 由可知：则 的终边所在的象限为第四象限 故选 ‎7.已知，，，若，则等于（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据向量的坐标运算法则,依据题意列出等式求解.‎ ‎【详解】由题知:,,,‎ 因为,‎ 所以,‎ 故,‎ 故选:A.‎ ‎【点睛】本题考查向量的坐标运算,属于基础题.‎ ‎8.（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ 分析：利用诱导公式和两角差的余弦函数，即可化简求值．‎ 详解：由题意 ‎ ‎，故选B．‎ 点睛：本题考查了三角函数的化简求值，其中解答中涉及到三角函数的诱导公式和两角差的余弦函数的应用，其中熟记三角函数的恒等变换的公式是解答的关键，试题比较基础，属于基础题．‎ ‎9. 某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40,50), [50,60), [60,70), [70,80), [80,90), [90,100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（ ）‎ A. 588 B. ‎480 ‎C. 450 D. 120‎ ‎【答案】B ‎【解析】‎ 试题分析：根据频率分布直方图，得；该模块测试成绩不少于60分的频率是1-（0.005+0.015）×10=0.8，∴对应的学生人数是600×0.8=480‎ 考点：频率分布直方图 ‎10.定义运算，设，若，，，则的值域为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【详解】由题意，‎ ‎ 由于与都是周期函数，且最小正周期都是，‎ ‎ 故只须在一个周期上考虑函数的值域即可，‎ ‎ 分别画出与的图象，如图所示，‎ ‎ 观察图象可得：的值域为，故选C.‎ ‎ ‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎11.的值为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 直接利用诱导公式化简求值.‎ ‎【详解】,‎ 故答案为:.‎ ‎【点睛】本题考查诱导公式的应用,属于基础题.‎ ‎12.设向量与向量共线，则实数等于__________．‎ ‎【答案】3‎ ‎【解析】‎ ‎【分析】‎ 利用向量共线坐标公式,列式求解.‎ ‎【详解】因为向量与向量共线,‎ 所以,‎ 故答案为:3.‎ ‎【点睛】本题考查向量共线的坐标公式,属于基础题.‎ ‎13. 将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为________.‎ ‎【答案】‎ ‎【解析】‎ ‎2本不同的数学书和1本语文书在书架上随机排成一行，所有的基本事件有（数学1，数学2，语文），（数学1，语文，数学2），（数学2，数学1，语文），（数学2，语文，数学1），（语文，数学1，数学2），（语文，数学2，数学1）共6个，其中2本数学书相邻的有（数学1，数学2，语文），（数学2，数学1，语文），（语文，数学1，数学2），（语文，数学2，数学1）共4个，故2本数学书相邻的概率 ． ‎ ‎14.已知函数y=sin（x+）（>0, -<）的图象如图所示，则=________________ . ‎ ‎【答案】‎ ‎【解析】‎ ‎【详解】由图可知，‎ 三、解答题：本大题天4小题，每小题10分，共40分.解答应写出文字说明、证明过程或演算步骤.‎ ‎15.从两个班中各随机抽取10名学生，他们的数学成绩如下，通过作茎叶图，分析哪个班学生的数学学习情况更好一些.‎ 甲班 ‎76‎ ‎74‎ ‎82‎ ‎96‎ ‎66‎ ‎76‎ ‎78‎ ‎72‎ ‎52‎ ‎68‎ 乙班 ‎86‎ ‎84‎ ‎62‎ ‎76‎ ‎78‎ ‎92‎ ‎82‎ ‎74‎ ‎88‎ ‎85‎ ‎【答案】茎叶图见解析，乙班 ‎【解析】‎ ‎【分析】‎ 根据表中数据作出茎叶图再依据茎叶图进行分析.‎ ‎【详解】根据表中数据,作出茎叶图如下:‎ 从这个茎叶图中可以看出,甲班成绩集中在70分左右,而乙班成绩集中在80左右,‎ 故乙班的数学成绩更好一些.‎ ‎【点睛】本题考查画茎叶图,也考查茎叶图的应用,属于基础题.‎ ‎16.求函数的单调递增区间.‎ ‎【答案】（）‎ ‎【解析】‎ 分析】‎ 先化简函数得到,再利用复合函数单调性原则结合整体法求单调区间即可.‎ ‎【详解】,‎ 令,则,‎ 因为是的一次函数,且在定义域上单调递增,‎ 所以要求的单调递增区间,即求的单调递减区间,‎ 即(),‎ ‎∴(),‎ 即(),‎ ‎∴函数的单调递增区间为().‎ ‎【点睛】本题考查求复合型三角函数的单调区间,答题时注意,复合函数的单调性遵循“同增异减”法则.‎ ‎17.已知.‎ ‎(1)求与的夹角；‎ ‎(2)求.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由得到，又代入夹角公式 ‎，求出的值；‎ ‎（2）利用公式进行模的求值.‎ ‎【详解】（1）因为，所以，‎ 因为，因为，所以.‎ ‎（2）.‎ ‎【点睛】本题考查数量积的运算及其变形运用，特别注意之间关系的运用与转化，考查基本运算能力.‎ ‎18.已知.‎ ‎（1）求函数的最小正周期；‎ ‎（2）求函数在闭区间上的最小值并求当取最小值时，的取值.‎ ‎【答案】（1）；（2），‎ ‎【解析】‎ ‎【分析】‎ ‎(1)先化简,再求最小正周期;‎ ‎(2)由,得,再结合的函数图像求最小值.‎ ‎【详解】(1)‎ ‎,‎ 即,‎ 所以的最小正周期是;‎ ‎(2)由(1)知,‎ 又由,得,‎ 所以当时,的最小值为,‎ 即时,的最小值为.‎ ‎【点睛】本题考查三角恒等变换,考查三角函数图像的性质应用,属于中档题.‎