- 2021-05-20 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
文科高考中关于异面直线所成角的常考题型
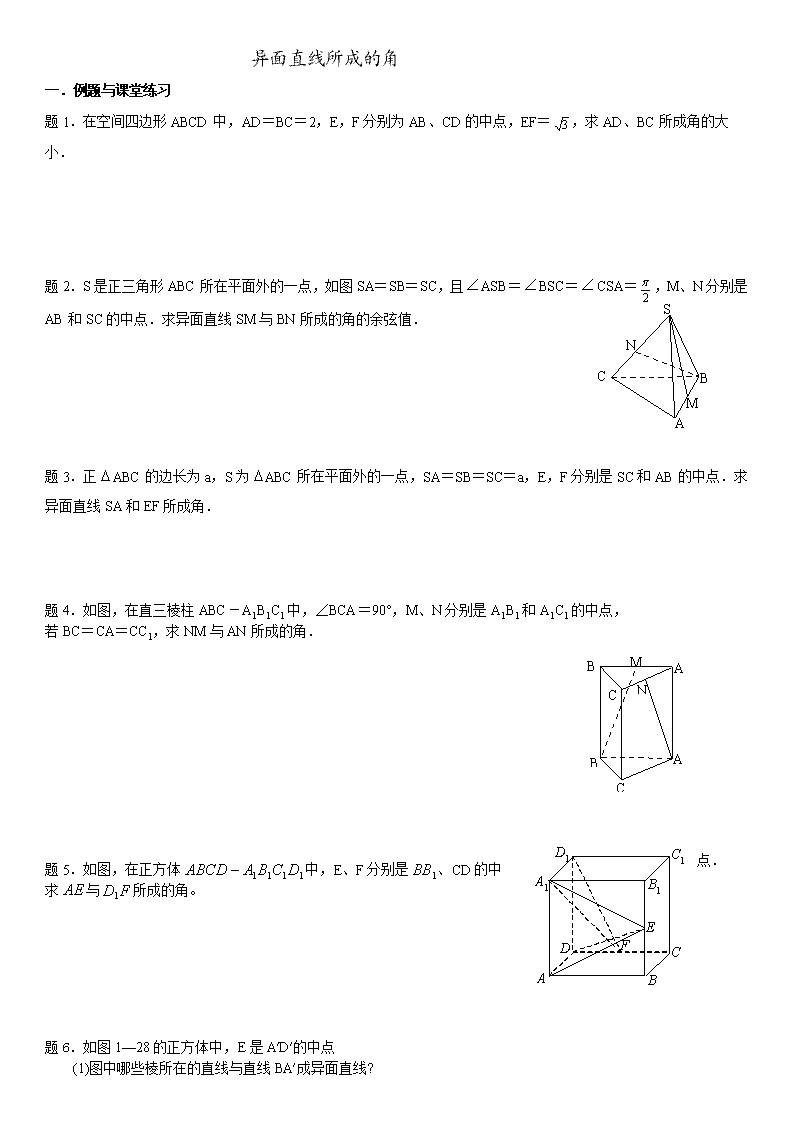
异面直线所成的角 一.例题与课堂练习 题1.在空间四边形ABCD中,AD=BC=2,E,F分别为AB、CD的中点,EF=,求AD、BC所成角的大小. B M A N C S 题2.S是正三角形ABC所在平面外的一点,如图SA=SB=SC,且ASB=BSC=CSA=,M、N分别是AB和SC的中点.求异面直线SM与BN所成的角的余弦值. 题3.正ABC的边长为a,S为ABC所在平面外的一点,SA=SB=SC=a,E,F分别是SC和AB的中点.求异面直线SA和EF所成角. 题4.如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,M、N分别是A1B1和A1C1的中点, 若BC=CA=CC1,求NM与AN所成的角. A C B N M A1 C1 B1 题5.如图,在正方体中,E、F分别是、CD的中点. 求与所成的角。 题6.如图1—28的正方体中,E是A′D′的中点 (1)图中哪些棱所在的直线与直线BA′成异面直线? B¢ (图1-28) A¢ A B C¢ D¢ C D F E (2)求直线BA′和CC′所成的角的大小; (3)求直线AE和CC′所成的角的正切值; (4)求直线AE和BA′所成的角的余弦值 【说明】(1)如图1—29,单独画出△A¢BF,使图中线段与角的数量关系较直观图中清楚,使计算更为方便和准确,这是立体几何中常用的重要方法; (2)解法中用余弦定理求cos∠A¢BF,其实有更简单方法,请找出简单方法 (3)如果用余弦定理求出角的余弦值为负数,应如何写答案? 异面直线所成的角的作业 一. 判断是非(下列命题中,正确的打“√”,错误的打“×”) (1)梯形的四个顶点在同一平面内; (2)对边相等的四边形是平行四边形; (3)平行于同一直线的两直线平行; (4)垂直于同一直线的两直线平行; (5)两条直线确定一个平面; (6)经过三点可以确定一个平面; (7)无公共点的两直线异面; (8)两异面直线无公共点; (9)两异面直线可以同时平行于一直线; (10)两异面直线可以同时垂直于一直线; (11)不同在一个已知平面内的两直线异面;(12)互相垂直的两条直线必可确定一平面 二. 选择题 1.没有公共点的两条直线的位置关系是( ) (A)平行 (B)异面 (C)平行或异面 (D)不能确定 2.分别在两相交平面内的两条直线的位置关系是( ) (A)异面 (B)平行 (C)平行或异面 (D)平行或异面或相交 3.两条异面直线指的是( ) (A)在空间不相交的两条直线(B)某一平面内的一条直线和这个平面外的一条直线 (C)分别位于两个不同平面的两条直线 (D)不同在任一平面内的两条直线 4.a、b是异面直线,b、c也是异面直线,那么a、c的位置是( ) (A)异面 (B)异面或平行 (C)异面或相交 (D)相交、平行或异面 B1 (第6题) A1 A B C1 D1 C D 5.说出正方体中各对线段的位置关系: (1) AB和CC1; (2)A1C和BD1; (3)A1A和CB1; (4)A1C1和CB1; (5)A1B1和DC; (6)BD1和DC. (第7题) F1 A B C D1 C1 A1 B1 B1 (第6题) A1 A B C1 D1 C D M N 6.在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是( ) 7.如图,A1B1C1—ABC是直三棱柱(三侧面为矩形),∠BCA=90°,点D1、F1 分别是A1B1、A1C1的中点若BC=CA=CC1,则BD1与AF1所成角的余弦值是( ) 8.正方体ABCD—A1B1C1D1中,直线BC1与AC (A)相交且垂直 (B)相交但不垂直 (C)异面且垂直 (D)异面但不垂直 9.设a、b、c是空间中的三条直线,下面给出四个命题: ①如果a⊥b、b⊥c,则a∥c; ②如果a和b相交,b和c相交,则a和c也相交; ③如果a、b是异面直线,c、b是异面直线,则a、c也是异面直线; ④如果a和b共面,b和c共面,则a和c也共面在上述四个命题中,真命题的个数是( ) (A)4 (B)3 (C)2 (D)1 (E)0 10.如果直线l和n是异面直线,那么和直线l、n都垂直的直线 (A)不一定存在 (B)总共只有一条 (C)总共可能有一条,也可能有两条 (D)有无穷多条 11.如图,四面体SABC的各棱长都相等,如果E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( ) (A)90° (B)60° (C)45° (D)30° F A B C E S (第11题)查看更多