- 2021-05-20 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】上海市松江区2019-2020学年高二下学期期末考试试题
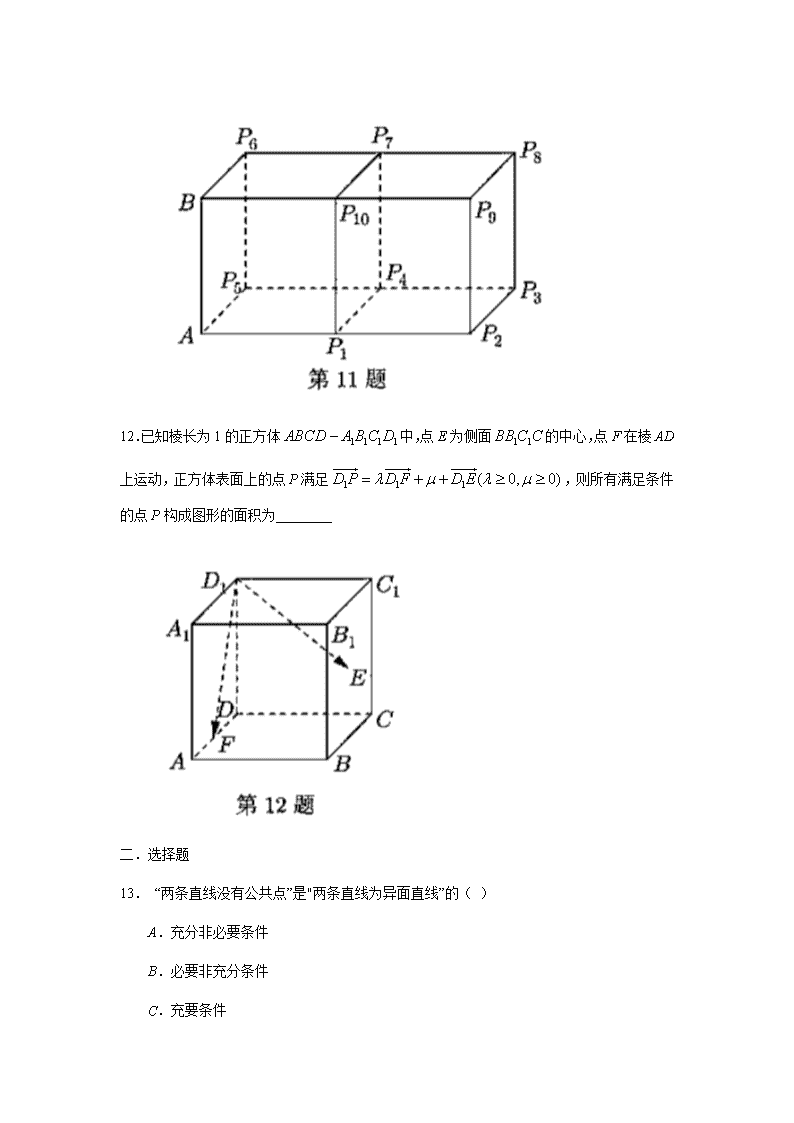
上海市松江区2019-2020学年高二下学期期末考试试题 一.填空题 1.已知正方体的棱长为a,异面直线BD与的距离为________ 2.若排列数 ,则m=________. 3.若关于x的一元二次方程(其中)有一个根为1+i (i是虚数单位),则q的值为________ 4.正三棱柱的侧棱长为4,底面边长为6,则此三棱柱的体积为________ 5.已知直线l的一个方向向量,平面α的一个法向量,若l⊥α,则m+n=________ 6.已知复数z满足,则(其中i是虚数单位)的最小值为________ 7.已知,则向量与的夹角是________ 8.二项式的展开式中,各项的系数之和为A,各项的二项式系数之和为B,且A+B=72,则n=________ 9.从分别标有数字1, 2, …, 9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到的2张卡片上数字的奇偶性不同的概率是________ 10.设球O的表面积为16π,圆是球O的一小圆, , A、B是圆上的两点,若A、B两点间的球面距离为,则________ 11.如图,两个棱长为1的正方体排成一个四棱柱, AB是一条侧棱, 是正方体其余的10个顶点,则的不同值的个数为________个 上海市松江区2019-2020学年高二下学期期末考试试题 一.填空题 1.已知正方体的棱长为a,异面直线BD与的距离为________ 2.若排列数 ,则m=________. 3.若关于x的一元二次方程(其中)有一个根为1+i (i是虚数单位),则q的值为________ 4.正三棱柱的侧棱长为4,底面边长为6,则此三棱柱的体积为________ 5.已知直线l的一个方向向量,平面α的一个法向量,若l⊥α,则m+n=________ 6.已知复数z满足,则(其中i是虚数单位)的最小值为________ 7.已知,则向量与的夹角是________ 8.二项式的展开式中,各项的系数之和为A,各项的二项式系数之和为B,且A+B=72,则n=________ 9.从分别标有数字1, 2, …, 9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到的2张卡片上数字的奇偶性不同的概率是________ 10.设球O的表面积为16π,圆是球O的一小圆, , A、B是圆上的两点,若A、B两点间的球面距离为,则________ 11.如图,两个棱长为1的正方体排成一个四棱柱, AB是一条侧棱, 是正方体其余的10个顶点,则的不同值的个数为________个 12.已知棱长为1的正方体中,点E为侧面的中心,点F在棱AD上运动,正方体表面上的点P满足,则所有满足条件的点P构成图形的面积为________ 二.选择题 13. “两条直线没有公共点”是"两条直线为异面直线”的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件 14.某中学采用系统抽样方法,从该校高一年级全体400名学生中抽25名学生做牙齿健康检查,现将400名学生从1到400进行编号,求得间隔数,即每16人抽取—个人,在1—16中随机抽取一个数,如果抽到的是7,则从33—48这16个数中应取的数是( ) A.40 B. 39 C.38 D. 37 15.设a、b是两条不同的直线, α、β是两个不同的平面,则下列四个命题正确的是( ) A.若,则 B.若,则 C.若,则 D.若,则 16.已知集合,从这三个集合中各取一个元素构成空间直角坐标系中的点的坐标,则不同点的坐标个数为( ) A. 36 B.35 C.34 D. 33 三.解答题 17.已知复数 (其中i是虚数单位). (1)求z: (2)若,求a的取值范围 18.已知圆锥的顶点为P,底面圆心为O,母线长为4, 是底面半径,且为线段AB的中点,如图所示. (1)求圆锥的表面积; (2)求异面直线PM与OB所成的角的大小. 19.为了促进消费回补和潜力释放,上海市政府举办“2020五五购物节”活动,某商家提供1000台吸尘器参加此项活动,其中豪华型吸尘器400台,普通型吸尘器600台. (1)豪华型吸尘器前6天的销量分别为: 9、12.x、y、10、10 (单位:台) , 把这6个数据看作一个总体,其均值为10,方差为3,求的值; (2)若用分层抽样的方法在这批吸尘器中抽取一个容量为25的样本,将该样本看成一个总体,从中任取2台吸尘器,求至少有1台豪华型吸尘器的概率(用最简分数表示). 20.如图所示,已知三棱柱的侧棱与底面垂直,,AB⊥AC, M是的中点, N是BC的中点,点P在直线上,且满足. (1)证明: PN⊥AM; (2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角取得最大值时的正切值; (3)若平面PMN与平面ABC所成的二面角为45°,试确定点P的位置. 21.我们称元有序实数组为n维向量, 为该向量的范数,已知n维向量,其中,记范数为奇数的n维向量的个数为,这个向量的范数之和为. (1)求和的值; (2)求值; (3)当n为奇数时,证明:.查看更多