六年级总复习教案《图形的认识》

六年级总复习教案《图形的认识》

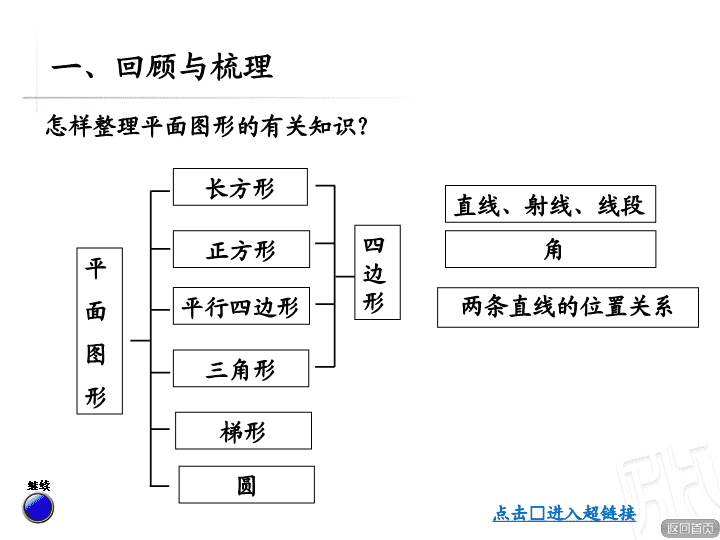
图形的认识整理与复习 应用与反思 讨论与交流 回顾与梳理 总结与评价 一、回顾与梳理 怎样整理平面图形和立体图形的有关知识？ 回顾整理要求： 2. 把整理的结果用表格、流程图、树状图等自己喜欢的 方式表示出来。 1. 小组合作，对平面图形的相关知识进行系统地回顾与整理。 平 面 图 形 直线、射线、线段 角 两条直线的位置关系 怎样整理平面图形的有关知识？ 三角形 正方形 长方形 平行四边形 梯形 圆 四边形 点击 □进入超链接 继续 一、回顾与梳理 想一想：直线、射线和线段有什么联系？ 直线 射线 线段 一、回顾与梳理 直线、射线和线段 : 射线 线段 直线 不同点 相同点 名称 直线、射线和线段的关系 能否延长 能 不能 不能 能否测量长度 1 个 无 都是直 直的线 端点个数 2 个 可以向两端 无限延长 可以向一端 无限延长 不能向两端无限延长 返回 一、回顾与整理 角 射线 两条 锐角 直角 钝角 平角 周角 小于 90° 90° 大于 90° 小于 180° 180° 360° 想一想：角的大小与什么有关？ 返回 一、回顾与梳理 角 : 从一个顶点出发 两直线的 位置关系 相交 不相交 垂直 不垂直 平行 返回 同一个平面内两条直线的位置关系 : 一、回顾与梳理 四个角都是直角。 ɑ b 两组对边平行且相等； C = （ ɑ ＋ b ） ×2 S = ɑ b 一、回顾与梳理 长方形： 返回 四个角都是直角。 ɑ 四条边都相等； C = 4 ɑ S = ɑ ² 一、回顾与梳理 正方形： 返回 相对的角相等。 h 两组对边平行且相等； S = ɑ h 一、回顾与梳理 平行四边形： 返回 ɑ b h 只有一组对边平行。 S = （ ɑ ＋ b ） h ÷2 一、回顾与梳理 梯形： 返回 ɑ 内角和是 180 ° ； 任意两边长度和大于第三边。 具有稳定性； ɑ h 三角形有三条边、三个顶点； S = ɑh ÷2 怎样给三角形分类呢？ 一、回顾与梳理 三角形： 锐角三角形 直角三角形 钝角三角形 等边三角形 等腰三角形 三角形 按角分类 按边分类 怎样给三角形分类呢 ? 返回 一、回顾与梳理 r 圆有无数条半径，有无数条直径。 S = πr ² 返回 o d 所有的直径都相等； 圆是轴对称图形，每一条直径所在的直线都是它的对称轴。 同一个圆中 d = 2 r r = d ÷2 C = πd 一、回顾与梳理 圆： 直径是半径的 2 倍。 所有的半径都相等； 名称 特点 计算公式 长方形 正方形 平 行 四边形 三角形 梯 形 圆 形 想一想 , 填一填。 平面图形 对边相等，四个角都是直角。 四条边都相等，四个角都是直角。 对边平行且相等，相对的角相等。 由三条线段围成，内角和是 180 度。 只有一组对边平行的四边形。 在同圆（等圆）中，所有的半径都相等，所有的直径都相等。 C=2( ɑ +b) S=ab C=4a    S=ɑ 2 S=ɑh S=ɑh÷2 S=  ( ɑ+b ) h ÷2 d=2r C=2πr C=πd    S=πr 2 一、回顾与梳理 你能把它们分分类吗？ 线段围成 曲线围成 一、回顾与梳理 返回 四边形 平行四边形 长方形 正方形 梯形 等腰梯形 直角梯形 你能给四边形分分类吗？ 一、回顾与梳理 四边形之间的关系 当梯形的上底等于 0 时，就变成了三角形。 一、回顾与梳理 当梯形的上、下底相等时，就变成了平行四边形。 四边形之间的关系 一、回顾与梳理 一、回顾与整理 当平行四边形的四个角都是直角时，就变成了长方形。 四边形之间的关系 当长方形的长和宽相等时，就变成了正方形。 返回 立 体 图 形 怎样整理立体图形的有关知识？ 长方体 圆柱 正方体 圆锥 一、回顾与梳理 继续 点击 □进入超链接 ɑ h b 长方体有 6 个面、 12 条棱和 8 个顶点； 6 个面都是长方形（特殊情况下有两个相对的面是正方形），相对的面完全相同，相对 4 条棱的长度相等。 S = （ ɑ b ＋ ɑ h ＋ bh ） ×2 V = ɑ b h 返回 一、回顾与梳理 长方体： ɑ 正方体有 6 个面、 12 条棱和 8 个顶点； S = 6 ɑ ² V = ɑ ³ 返回 6 个面都是正方形； 每个面都相等； 12 条棱都相等。 一、回顾与梳理 正方体： S S 表 = 2 S 底 ＋ S 侧 V = Sh h 上、下两个面都是圆，并且大小相等 ; S 侧 = Ch 返回 一、回顾与梳理 圆柱： 侧面是一个曲面。 h 底面是个圆。 V = Sh S 侧面是一个曲面。 返回 一、回顾与梳理 圆锥： 名 称 特点 计算公式 长方体 正方体 圆 柱 圆 锥 6 个面是长方形（特殊情况有两个对面是正方形）对面相等； 12 条棱，相对 4 条棱长度相等； 8 个顶点。 6 个面都相等，都是正方形； 12 条棱都相等； 8 个顶点。 上下两个面是完全相同的圆形，侧面是一个曲面，上下一样粗。 底面是一个圆，侧面展开是扇形，只有一条高。 S= 2 （ ɑb+ɑh+bh ） V = Sh V = π r 2 h S= 6 ɑ 2 想一想 , 填一填。 立体图形 V= ɑbh V= ɑ 3 S 侧 = 2 π rh S 表 = 2 π rh + 2 π r 2 一、回顾与梳理 你能把它们分分类吗？ 所有的面都是平面 有一个面是曲面 一、回顾与梳理 当长方体的长、宽、高相等时，就变成了正方体。 正方体是特殊的长方体。 立体图形之间的关系 长方体 正方体 一、回顾与梳理 当圆柱的上底面的面积等于 0 时，就变成了圆锥。 立体图形之间的关系 一、回顾与梳理 返回 二、讨论与交流 ● 我们是从哪几个方面研究平面图形特征的？立体图形呢？ 平面图形的特点主要从线、角来研究的。 立体图形的特点主要从点、线、面来研究的。 （ 1 ）一条射线长 3 厘米。　　　　　　　　　　（　）   （ 2 ）圆柱体的体积等于圆锥体的 3 倍。 　　 　（　）   （ 3 ）小冬用一个能放大 10 倍的放大镜去看一个 角，结果这个角的大小放大了 10 倍。　 （　）   （ 4 ）圆柱的侧面展开后是一个正方形，那么它的底面周长和 高一定相等。 （ ） （ 5 ）正方体的棱长总和是 48 厘米，它的每条棱长是 4 厘米。 （ ） 1. 火眼金睛辨对错。 × √ × × √ 三、应用与反思 2 . 三、应用与反思 自来水公司计划经过 P 点铺两条管道，一条管道要与 a 管道平行，另一条与 a 管道相连且最省料。请画出这两条管道所在的位置。 3. 三、应用与反思 想一想，将下列平面图形以一条边为轴旋转一周，会形成什么样的空间图形，用线连一连。 三、应用与反思 3. 想一想，下面的平面图形，以它的一条边为轴旋转一周，会形成什么样的空间图形，用线连一连。 宝剑锋从磨砺出，梅花香自苦寒来！