- 2021-05-19 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三年级上册数学一课一练-4.24认识面积
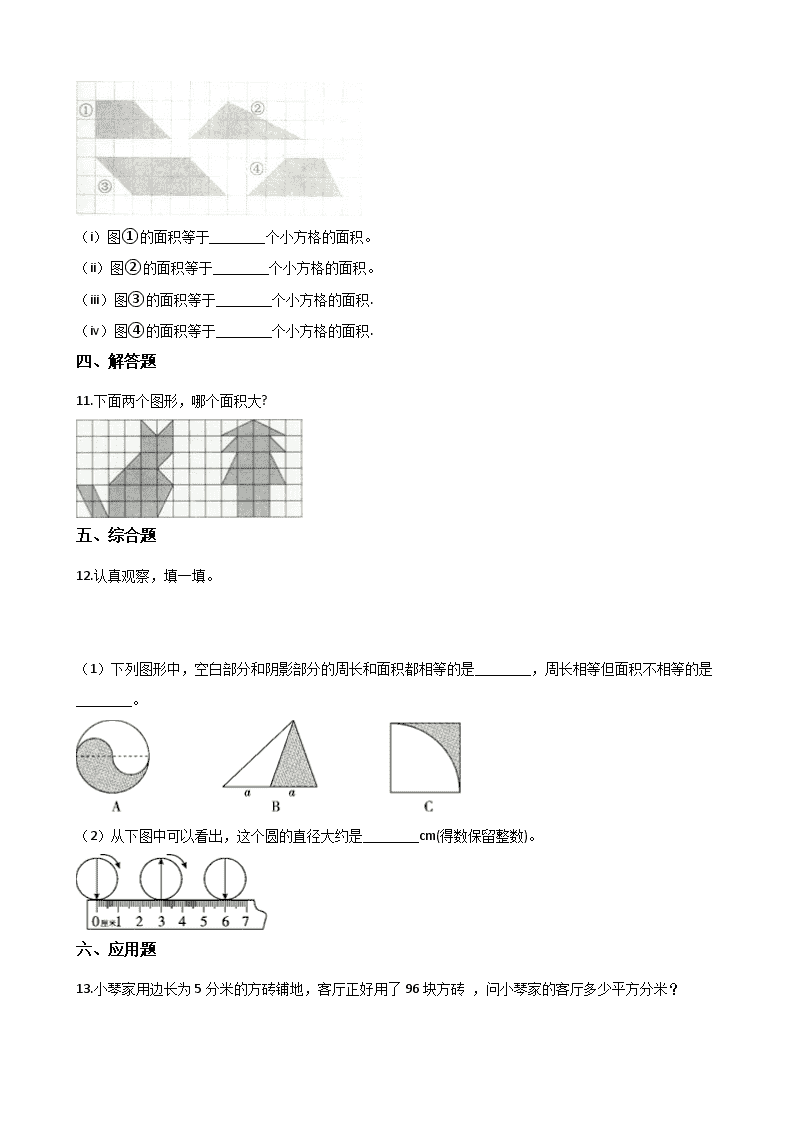
三年级上册数学一课一练-4.24认识面积 一、单选题 1.一个长方形和一个圆的周长相等,它们的面积相比,( )。 A. 长方形=圆 B. 圆<长方形 C. 圆>长方形 2.一个圆的周长与一个正方形的周长相等,那么它们的面积大小比较( ) A. 两个面积一样大 B. 圆面积大 C. 正方形面积大 D. 不能确定 3.一个正方形的周长与一个圆的周长相等,它们的面积大小是( ) A. 相等 B. 圆的面积大 C. 正方形的面积大 D. 无法比较 4.如果四边形ABCD是长方形,下面说法错误的有( ) A. 三角形BCE面积>三角形BCF面积 B. 三角形BCE面积=三角形BCF面积 C. 三角形BOE面积=三角形COF面积 D. 三角形BCE面积是长方形ABCD面积的一半 二、判断题 5.一个角的面积是10平方分米。( ) 6.(2014·重庆云阳)下面四个图涂色部分的面积相等,周长也相等。(判断对错) 7.当圆的直径和正方形的边长相等时,正方形的面积比圆的面积大. 三、填空题 8.把4个面积是1平方分米的小正方形拼成一个大的正方形,这个大正方形的面积是________平方分米,周长是________分米。 9.如图,两个大三角形等底等高,有部分重叠在一起,甲、乙两个图形的面积相比,甲________乙.(填“大于”“小于”“=”) 10.数数填填。 (i)图①的面积等于________个小方格的面积。 (ii)图②的面积等于________个小方格的面积。 (iii)图③的面积等于________个小方格的面积. (iv)图④的面积等于________个小方格的面积. 四、解答题 11.下面两个图形,哪个面积大? 五、综合题 12.认真观察,填一填。 (1)下列图形中,空白部分和阴影部分的周长和面积都相等的是________,周长相等但面积不相等的是________。 (2)从下图中可以看出,这个圆的直径大约是________cm(得数保留整数)。 六、应用题 13.小琴家用边长为5分米的方砖铺地,客厅正好用了96块方砖 ,问小琴家的客厅多少平方分米? 参考答案 一、单选题 1.【答案】 C 【解析】【解答】假设它们的周长是6.28厘米,则长+宽:6.28÷2=3.14(厘米),长方形的长和宽越接近,它的面积越大 所以长方形的长可以为1.56厘米,1.58厘米,长方形的面积:1.56×1.58=2.4648(平方厘米) 圆的面积:6.28÷3.14÷2=1(厘米),3.14×12=3.14(平方厘米),2.4648<3.14,所以周长相等时圆的面积大于长方形的面积. 故选:C. 【分析】本题考点:面积及面积的大小比较. 周长相等的情况下利用假设的方法分别求出它们的面积相比较,这是一种常用的方法. 假设它们的周长都是6.28厘米,分别依据各自的周长公式求出长方形的长和宽,圆的半径,进而依据各自的面积公式即可求出它们的面积,进而比较出它们的面积的大小. 2.【答案】 B 【解析】【解答】解:假设圆的周长和正方形的周长是12.56厘米. 则正方形的边长a=c÷4═12.56÷4=3.14(厘米) 正方形的面积S=a2=3.14×3.14=9.8596(平方厘米) 圆的半径r=C÷2π=12.56÷(2×3.14)=2(厘米) 圆的面积S=πr2=3.14×22=12.56(平方厘米) 12.56>9.8596 则圆的面积大于正方形的面积. 故选:B. 【分析】这道题中圆和正方形的周长没有说明具体是多少,要比较它们的面积不好比较,因此,可以把它们的周长假设成一个数,根据“a=c÷4和r=c÷2π”算出正方形的边长和圆的半径,再根据正方形的面积公式和圆的面积公式,算出它们的面积后去比较大小,最后得出答案.像这样没有具体数字而要求比较大小的题目,可以采用“假设法”,也就是举例子,放到具体的题目中去比较. 3.【答案】B 【解析】【解答】解:设周长是c,则正方形的边长是:C÷4= ,圆的半径是:C÷2π= , 则圆的面积为:π×( )2= , 正方形的面积为: × = , 因为 > ,所以圆的面积大; 故选:B. 【分析】周长相等的正方形和圆,圆的面积比正方形的面积大.可以通过举例证明,设周长是C,则正方形的边长是C÷4,圆的半径是C÷2π;根据它们的面积公式求出它们的面积,进行比较.此题主要考查周长相等的正方形和圆,圆的面积比正方形的面积大. 4.【答案】 A 【解析】【解答】解:根据等底等高的三角形面积相等,可知三角形BCE面积=三角形BCF面积, 由等量关系可得三角形BOE面积=三角形COF面积, 根据等底等高的三角形面积是长方形面积的一半,可知三角形BCE面积是长方形ABCD面积的一半, 故选项B、C、D的说法是正确的,选项A的说法是错误的. 故选:A. 【分析】根据等底等高的三角形面积相等,以及等底等高的三角形面积是长方形面积的一半,以及等量关系即可求解. 二、判断题 5.【答案】 错误 【解析】【解答】角没有面积和周长 【分析】面积和周长都必须是在封闭的图形内 6.【答案】错误 【解析】【解答】由图可知:空白部分的面积都是一个大圆的面积减去一个小黑圆的面积,即空白部分的面积相等, 所以四个图形的阴影部分的面积都相等,但周长明显不等; 故答案为:错误. 【分析】考点:面积及面积的大小比较、圆、圆环的周长. 明确空白部分的面积都是一个大圆的面积减去一个小黑圆的面积,即空白部分的面积相等,是解答此题的关键. 由图可知:空白部分的面积都是一个大圆的面积减去一个小黑圆的面积,即空白部分的面积相等,因为大圆的面积相等,所以阴影部分的面积也相等,但是周长不相等;由此解答即可. 7.【答案】正确 【解析】【解答】解:假设圆的半径为r, 则圆的面积=πr2 , 正方形的边长=2r, 则正方形的面积=2r×2r, =4r2 , 又因4r2>πr2 , 所以一个圆的直径和一个正方形的边长相等,那么正方形的面积一定大于圆的面积. 故答案为:√. 【分析】圆的面积=πr2 , 正方形的面积=a2 , 可以假设出圆的半径,分别代入公式求出其面积,即可进行判断.此题主要考查圆和正方形的面积的计算方法的灵活应用. 三、填空题 8.【答案】4 ;8 【解析】【解答】4个小正方形两两并排构成一个大正方形,面积就是4个小正方形面积的和,大正方形的一条边由两个小正方形的边构成,所以边长是2分米,它的周长是8分米 【分析】要结合图形的变换来做题 9.【答案】= 【解析】【解答】解:因为两个大三角形等底等高,所以两个大三角形的面积相等,再都去掉重叠的部分; 所以甲、乙两个图形的面积相等; 故答案为:=. 【分析】因为两个大三角形等底等高,所以两个大三角形的面积相等,再都去掉重叠的部分,由此得出结论.本题主要是利用等底等高的三角形的面积相等解答. 10.【答案】6 ;6 ;10 ;7 【解析】【解答】6 6 10 7 【分析】 用数方格的方法求解,先数出整方格的个数,再数出不是整方格的个数,进而确定出图形大约有几个方格,再乘上每个方格的面积即可. 面积及面积的大小比较.解决此类题要注意认真分析图形,弄清图形所占的整方格数,然后再计算图形的面积即可. 四、解答题 11.【答案】答:第一个图形的面积大。 【解析】【分析】本题考点:面积及面积的大小比较. 关键是先求出每组中图形的面积,再比较. 设1个小正方形的面积为a,分别数出小正方形的个数,即先分别算出每组中图形的面积,再进行比较即可. 五、综合题 12.【答案】(1)A;C (2)2 【解析】【分析】(1)选项A,阴影部分和空白部分的周长都等于大圆周长的一半+小圆的周长,阴影部分和空白部分的面积都等于大圆面积的一半;选项B,阴影部分和空白部分的面积相等,因为它们是等底等高的两个三角形,周长不相等,空白部分的周长大于阴影部分的周长;选项C,空白部分和阴影部分的周长都等于正方形的两条边长的和+圆弧的长度,空白部分的面积大于阴影部分的面积;(2)观察图可知,这个圆转动一圈的长度是6厘米,要求这个圆的直径,用一圈的长度÷3.14,结果保留整数即可. 六、应用题 13.【答案】 解:5×96=480(平方分米) 答:小琴家的客厅480平方分米 【解析】【分析】通过生活中的实际问题,认识和学习了面积的知识 查看更多