- 2021-05-06 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年福建省厦门市湖里区五缘实验学校八年级(下)期末数学试卷 (解析版)
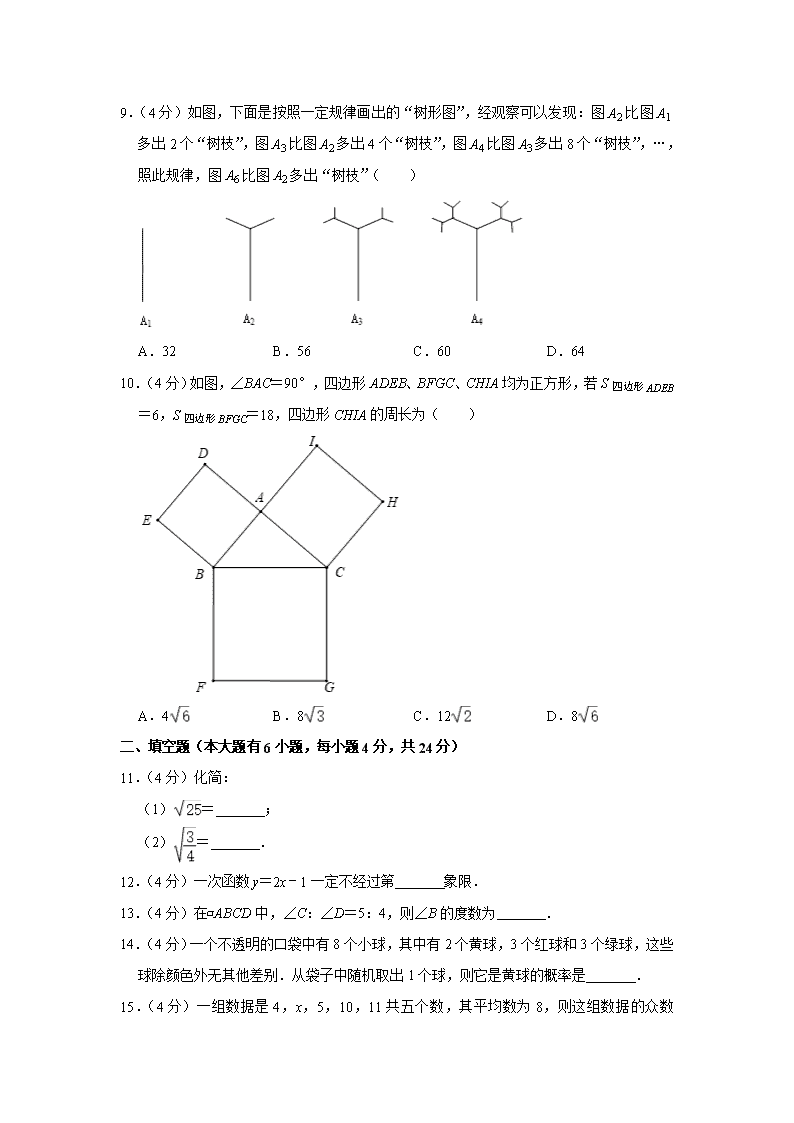
2019-2020学年福建省厦门市湖里区五缘实验学校八年级(下)期末数学试卷 一、选择题(共10小题,每小题4分,满分40分) 1.(4分)要使式子有意义,则x的值可以是( ) A.2 B.0 C.1 D.9 2.(4分)下列各式中,y随x的变化关系式是正比例函数的是( ) A.y=2x B.y= C.y=x﹣1 D.y=x2﹣1 3.(4分)以下列各组数为边长,能构成直角三角形的是( ) A.1,2,3 B.2,3,4 C.2,2,3 D.1,2, 4.(4分)下列条件中,不能判定四边形ABCD是平行四边形的是( ) A.AB=CD,AD=BC B.AB∥CD,∠B=∠D C.AB∥CD,AD=BC D.AB∥CD,AB=CD 5.(4分)若方程x2+3x+c=0有实数根,则c的取值范围是( ) A.c≤ B.c≤ C.c≥ D.c≥ 6.(4分)正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( ) A. B. C. D. 7.(4分)反比例函数y=﹣,下列说法不正确的是( ) A.图象经过点(1,﹣3) B.图象位于第二、四象限 C.图象关于直线y=x对称 D.y随x的增大而增大 8.(4分)样本方差的计算公式S2=[(x1﹣20)2+(x2﹣20)2+…+(x30﹣20)2]中,数字30和20分别表示样本的( ) A.众数、中位数 B.方差、标准差 C.数据的个数、中位数 D.数据的个数、平均数 9.(4分)如图,下面是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出“树枝”( ) A.32 B.56 C.60 D.64 10.(4分)如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为( ) A.4 B.8 C.12 D.8 二、填空题(本大题有6小题,每小题4分,共24分) 11.(4分)化简: (1)= ; (2)= . 12.(4分)一次函数y=2x﹣1一定不经过第 象限. 13.(4分)在▱ABCD中,∠C:∠D=5:4,则∠B的度数为 . 14.(4分)一个不透明的口袋中有8个小球,其中有2个黄球,3个红球和3个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是黄球的概率是 . 15.(4分)一组数据是4,x ,5,10,11共五个数,其平均数为8,则这组数据的众数是 . 16.(4分)如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,若∠ADB=36°,则∠E= °. 三、解答题(本大题有9小题,共86分) 17.(18分)(1)计算:; (2)计算:; (3)解方程:2x2﹣4x+1=0. 18.(7分)如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠A=∠C. 19.(7分)2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的5名选手的复赛成绩如图所示. (1)根据图示补全下表; 平均数(分) 中位数(分) 众数(分) A队 83 85 B队 95 (2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好; (3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定. 20.(8分)如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(2,3),B(﹣3,n)两点,与x轴交于点C. (1)求直线和双曲线的函数关系式. (2)若kx+b﹣<0,请根据图象直接写出x的取值范围. 21.(8分)如图,BD为▱ABCD的对角线,BD⊥AD,延长AD到点E,使得DE=AD,连接CE. (1)求证:四边形BCED是矩形; (2)若四边形BCED的周长是6,AB=5,求四边形BCED的面积. 22.(8分)如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边AB上距直角顶点B10米远的点D处同时开始测量,点C为终点.小娟沿D→B→C的路径测得所经过的路程是15米 ,小燕沿D→A→C的路径测得所经过的路程也是15米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由? 23.(9分)某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同. (1)求该家具商场计划购进的餐桌、餐椅的进价分别为多少元? (2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少? 24.(9分)如图,在△ABD中,AB=AD,将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE. (1)依题意补全图形; (2)判断∠DFC与∠BAE的大小关系并加以证明; (3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值. 25.(12分)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). (1)当t为何值时,四边形PQDC是平行四边形. (2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2? (3)是否存在点P,使△PQD是等腰三角形(不考虑QD=PD)?若存在,请求出所有满足要求的t的值,若不存在,请说明理由. 2019-2020学年福建省厦门市湖里区五缘实验学校八年级(下)期末数学试卷 参考答案与试题解析 一、选择题(共10小题,每小题4分,满分40分) 1.(4分)要使式子有意义,则x的值可以是( ) A.2 B.0 C.1 D.9 【分析】根据二次根式的意义,被开方数大于等于0,即可求得. 【解答】解:依题意得:x﹣5≥0,解得:x≥5. 观察选项,只有选项D符合题意. 故选:D. 2.(4分)下列各式中,y随x的变化关系式是正比例函数的是( ) A.y=2x B.y= C.y=x﹣1 D.y=x2﹣1 【分析】根据正比例函数y=kx的定义条件:k为常数且k≠0,自变量次数为1,判断各选项,即可得出答案. 【解答】A、y=2x符合正比例函数的定义,故本选项正确; B、y=自变量次数不为1,故本选项错误; C、y=x﹣1是和的形式,故本选项错误; D、y=x2﹣1是二次函数,故本选项错误. 故选:A. 3.(4分)以下列各组数为边长,能构成直角三角形的是( ) A.1,2,3 B.2,3,4 C.2,2,3 D.1,2, 【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可. 【解答】解:A、12+22≠32; B、22+32≠42; C、22+22≠32; D、12+22=()2. 故选:D. 4.(4分)下列条件中,不能判定四边形ABCD是平行四边形的是( ) A.AB=CD,AD=BC B.AB∥CD,∠B=∠D C.AB∥CD,AD=BC D.AB∥CD,AB=CD 【分析】根据平行四边形的判断方法一一判断即可解决问题. 【解答】解:A、∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形, 故A可以判断四边形ABCD是平行四边形; B、∵AB∥CD,∴∠B+∠C=180°, ∵∠B=∠D, ∴∠D+∠C=180°, ∴AC∥BD, ∴四边形ABCD是平行四边形, 故B可以判断四边形ABCD是平行四边形; C、∵AB∥CD,AD=BC, ∴四边形ABCD可能是平行四边形,有可能是等腰梯形. 故C不可以判断四边形ABCD是平行四边形 D、∵AB∥CD,AB=CD, ∴四边形ABCD是平行四边形, 故D可以判断四边形ABCD是平行四边形; 故选:C. 5.(4分)若方程x2+3x+c=0有实数根,则c的取值范围是( ) A.c≤ B.c≤ C.c≥ D.c≥ 【分析】根据方程的系数结合根的判别式,即可得出△≥0,再求出不等式的解集即可. 【解答】解:∵方程x2+3x+c=0有实数根, ∴△=b2﹣4ac=32﹣4×1×c≥0, 解得:c≤, 故选:A. 6.(4分)正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( ) A. B. C. D. 【分析】直接利用正比例函数的性质得出k的取值范围,进而得出一次函数经过的象限. 【解答】解:∵正比例函数y=kx(k≠0)函数值y随x的增大而增大, ∴k>0, ∴y=kx﹣k的图象经过第一、三、四象限, 故选:B. 7.(4分)反比例函数y=﹣,下列说法不正确的是( ) A.图象经过点(1,﹣3) B.图象位于第二、四象限 C.图象关于直线y=x对称 D.y随x的增大而增大 【分析】通过反比例图象上的点的坐标特征,可对A选项做出判断;通过反比例函数图象和性质、增减性、对称性可对其它选项做出判断,得出答案. 【解答】解:由点(1,﹣3)的坐标满足反比例函数y=﹣,故A是正确的; 由k=﹣3<0,双曲线位于二、四象限,故B也是正确的; 由反比例函数图象的对称性,可知反比例函数y=﹣的图象关于y=x对称是正确的,故C也是正确的, 由反比例函数的性质,k<0,在每个象限内,y随x的增大而增大,不在同一象限,不具有此性质,故D是不正确的, 故选:D. 8.(4分)样本方差的计算公式S2=[(x1﹣20)2+(x2﹣20)2+…+(x30﹣20)2]中,数字30和20分别表示样本的( ) A.众数、中位数 B.方差、标准差 C.数据的个数、中位数 D.数据的个数、平均数 【分析】方差计算公式:S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],n表示样本容量,为平均数,根据此公式即可得到答案. 【解答】解:由于S2=[(x1﹣20)2+(x2﹣20)2+…+(x30﹣20)2],所以样本容量是30,平均数是20. 故选:D. 9.(4分)如图,下面是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出“树枝”( ) A.32 B.56 C.60 D.64 【分析】通过观察已知图形可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,以此类推可得:A6比图A2多出“树枝”4+8+16+32个 【解答】解:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,A6比图A2多出“树枝”4+8+16+32=60个, 故选:C. 10.(4分)如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为( ) A.4 B.8 C.12 D.8 【分析】由正方形的面积易求其边长AB2,BC2的长,再由勾股定理可求出AC的长,进而可求出四边形CHIA的周长. 【解答】解:∵四边形ADEB、BFGC均为正方形,S四边形ADEB=6,S四边形BFGC=18, ∴AB2=6,BC2=18, ∵∠BAC=90°, ∴AC2=18﹣6=12, ∴AC==2, ∴四边形CHIA的周长=4×2=8, 故选:B. 二、填空题(本大题有6小题,每小题4分,共24分) 11.(4分)化简: (1)= 5 ; (2)= . 【分析】利用算术平方根的定义计算即可. 【解答】解:(1)=5, 故答案为:5; (2)=, 故答案为:. 12.(4分)一次函数y=2x﹣1一定不经过第 二 象限. 【分析】根据一次函数图象与系数的关系求解. 【解答】解:∵k=2>0,b=﹣1<0, ∴一次函数图象在一、三、四象限,即一次函数图象不经过第二象限. 故答案为:二. 13.(4分)在▱ABCD中,∠C:∠D=5:4,则∠B的度数为 80° . 【分析】根据平行四边形的性质可得AD∥BC,∠B=∠D,利用平行线的性质可求解∠D的度数,进而可求解. 【解答】解:在▱ABCD中,AD∥BC,∠B=∠D, ∴∠C+∠D=180°, ∵∠C:∠D=5:4, ∴∠C=100°,∠D=80°, ∴∠B=80°. 故答案为80°. 14.(4分)一个不透明的口袋中有8个小球,其中有2个黄球,3个红球和3个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是黄球的概率是 . 【分析】用黄球的个数除以总球的个数即可得出黄球的概率. 【解答】解:∵不透明的口袋中有8个小球,其中有2个黄球,3个红球和3个绿球, ∴从袋子中随机取出1个球,则它是黄球的概率是=; 故答案为:. 15.(4分)一组数据是4,x,5,10,11共五个数,其平均数为8,则这组数据的众数是 10 . 【分析】首先根据平均数算出x的值,再根据众数的定义:一组数据中出现次数最多的数据叫做众数,可得答案. 【解答】解:根据题意,得:4+x+5+10+11=5×8, 解得x=10, 所以这组数据为4、5、10、10、11, 则这组数据的众数为10, 故答案为:10. 16.(4分)如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,若∠ADB=36°,则∠E= 18 °. 【分析】连接AC,由矩形性质可得∠E=∠DAE、BD=AC=CE,知∠E=∠CAE,而∠ADB=∠CAD=36°,可得∠E度数. 【解答】解:连接AC, ∵四边形ABCD是矩形, ∴AD∥BE,AC=BD,且∠ADB=∠CAD=36°, ∴∠E=∠DAE, 又∵BD=CE, ∴CE=CA, ∴∠E=∠CAE, ∵∠CAD=∠CAE+∠DAE, ∴∠E+∠E=36°, ∴∠E=18°. 故答案为:18 三、解答题(本大题有9小题,共86分) 17.(18分)(1)计算:; (2)计算:; (3)解方程:2x2﹣4x+1=0. 【分析】(1)先算乘法,再合并同类二次根式即可; (2)先根据平方差公式和完全平方公式进行计算,再合并同类二次根式即可; (3)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可. 【解答】解:(1) =2﹣6+3 =﹣4+3; (2) =1﹣3﹣12+4﹣1 =﹣15+4; (3)2x2﹣4x+1=0, 2x2﹣4x=﹣1, x2﹣2x=﹣, x2﹣2x+1=﹣+1, (x﹣1)2=, x﹣1=, x1=,x2=. 18.(7分)如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠A=∠C. 【分析】连接BD,利用SSS证得△ABD≌△CBD,得出答案即可. 【解答】证明:如图, 在△ABD和△CBD中, ∴△ABD≌△CBD ∴∠A=∠C. 19.(7分)2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的5名选手的复赛成绩如图所示. (1)根据图示补全下表; 平均数(分) 中位数(分) 众数(分) A队 83 85 85 B队 83 80 95 (2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好; (3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定. 【分析】(1)根据图示补充即可; (2)两队成绩的平均分一样,但A队成绩的中位数高,故A队成绩较好; (3)分别计算两队的方差,方差小的成绩较为稳定. 【解答】解:(1)补全如表: 平均数(分) 中位数(分) 众数(分) A队 83 85 85 B队 83 80 95 (2)两队成绩的平均分一样,但A队成绩的中位数高,故A队成绩较好; (3), , 两队成绩的方差分别是26,106, 因此A队选手成绩较为稳定. 20.(8分)如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(2,3),B(﹣3,n)两点,与x轴交于点C. (1)求直线和双曲线的函数关系式. (2)若kx+b﹣<0,请根据图象直接写出x的取值范围. 【分析】(1)先把A点坐标代入中得m=6,则反比例函数解析式为,再利用反比例函数解析式确定B(﹣3,﹣2),然后利用待定系数法求出一次函数解析式为y=x+1; (2)观察函数图象,写出一次函数图象在反比例函数图象下方所对应的自变量的范围即可. 【解答】解:(1)将A(2,3)代入中得m=6, ∴, ∴n=, ∴B(﹣3,﹣2), 将A(2,3),B(﹣3,﹣2)代入y=kx+b中得: , 解得:k=1,b=1, ∴y=x+1; (2)由图象可知,当0<x<2或x<﹣3时,直线落在双曲线的下方, 所以关于x的不等式kx+b﹣<0的解集是0<x<2或x<﹣3. 21.(8分)如图,BD为▱ABCD的对角线,BD⊥AD,延长AD到点E,使得DE=AD,连接CE. (1)求证:四边形BCED是矩形; (2)若四边形BCED的周长是6,AB=5,求四边形BCED的面积. 【分析】(1)证四边形BCED是平行四边形,由∠BDE=90°,即可得出四边形BCED是矩形; (2)由矩形的性质得∠DBC=90°,BC+BD=3,则(BC+BD)2=45①,BC2+BD2=CD2=AB2=25②,①﹣②得2BC×BD=20,则BC×BD=10,即可得出答案. 【解答】(1)证明:∵四边形ABCD是平行四边形, ∴CD=AB,AD=BC,AD∥BC, ∵DE=AD, ∴DE=BC, ∴四边形BCED是平行四边形, 又∵BD⊥AD, ∴∠BDE=90°, ∴四边形BCED是矩形; (2)解:∵四边形BCED是矩形,四边形BCED的周长是6, ∴∠DBC=90°,BC+BD=3, ∴(BC+BD)2=45①,BC2+BD2=CD2=AB2=25②, ①﹣②得:2BC×BD=20, ∴BC×BD=10, ∴四边形BCED的面积=BC×BD=10. 22.(8分)如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边AB上距直角顶点B10米远的点D处同时开始测量,点C为终点.小娟沿D→B→C的路径测得所经过的路程是15米,小燕沿D→A→C的路径测得所经过的路程也是15米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由? 【分析】设BC=a(m),AC=b(m),AD=x(m)根据勾股定理即可得到结论. 【解答】解:Rt△ABC中,∠B=90°, 设BC=a(m),AC=b(m),AD=x(m) 则10+a=x+b=15(m), ∴a=5(m),b=15﹣x(m) 又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2, ∴(10+x)2+52=(15﹣x)2, 解得:x=2,即AD=2(米) ∴AB=AD+DB=2+10=12米,BC=5米,AC=,米 答:这个直角三角花台底边上的高为米. 23.(9分)某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同. (1)求该家具商场计划购进的餐桌、餐椅的进价分别为多少元? (2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少? 【分析】 (1)根据用600元购进的餐桌数量与用160元购进的餐椅数量相同,可以得到相应的分式方程,然后即可得到该家具商场计划购进的餐桌、餐椅的进价分别为多少元; (2)根据题意,可以得到利润和购买餐桌数量的函数关系,再根据题意,利用一次函数的性质,即可得到该商场怎样进货,才能获得最大利润,最大利润是多少. 【解答】解:(1)设每张餐桌的价格为a元,则每张餐椅的价格为(a﹣110)元, , 解得,a=150 经检验,a=150是原分式方程的解, 则a﹣110=40, 答:该家具商场计划购进的餐桌、餐椅的进价分别为150元和40元; (2)设购进餐桌x张,则购进餐椅(5x+20)张,销售利润为W元, 由题意得:x+5x+20⩽200, 解得,x⩽30 W=x•(500﹣150﹣4×40)+x•(270﹣150)+(5x+20﹣x×4)×(70﹣40)=245x+600, ∵k=245>0, ∴W随x的增大而增大, ∴当x=30时,W取得最大值,最大值为7950.此时5x+20=170, 答:购进餐桌30张、餐椅170张时,才能获得最大利润,最大利润是7950元. 24.(9分)如图,在△ABD中,AB=AD,将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE. (1)依题意补全图形; (2)判断∠DFC与∠BAE的大小关系并加以证明; (3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值. 【分析】(1)将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE,据此画图即可; (2)根据△ABE≌△CBE(SAS),可得∠BAE=∠BCE.再根据AD∥BC,可得∠DFC=∠BCE,进而得出∠DFC=∠BAE; (3)连接CG,AC,根据EC+EG≥CG可知,CG长就是EA+EG的最小值,根据△ACD为边长为2的等边三角形,G为AD的中点,运用勾股定理即可得出CG=,进而得到EA+EG的最小值. 【解答】解:(1)如图所示: (2)判断:∠DFC=∠BAE. 证明:∵将△ABD沿BD翻折,使点A翻折到点C. ∴BC=BA=DA=CD. ∴四边形ABCD为菱形. ∴∠ABD=∠CBD,AD∥BC. 又∵BE=BE, ∴△ABE≌△CBE(SAS). ∴∠BAE=∠BCE. ∵AD∥BC, ∴∠DFC=∠BCE. ∴∠DFC=∠BAE. (3)如图,连接CG,AC. 由轴对称的性质可知,EA=EC, ∴EA+EG=EC+EG, 根据EC+EG≥CG可知,CG长就是EA+EG的最小值. ∵∠BAD=120°,四边形ABCD为菱形, ∴∠CAD=60°. ∴△ACD为边长为2的等边三角形. 又∵G为AD的中点, ∴DG=1, ∴Rt△CDG中,由勾股定理可得CG=, ∴EA+EG的最小值为. 25.(12分)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). (1)当t为何值时,四边形PQDC是平行四边形. (2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2? (3)是否存在点P,使△PQD是等腰三角形(不考虑QD=PD)?若存在,请求出所有满足要求的t的值,若不存在,请说明理由. 【分析】(1)由题意已知,AD∥BC,要使四边形PQDC是平行四边形,则只需要让QD=PC即可,因为Q、P点的速度已知,AD、BC的长度已知,要求时间,用时间=路程÷速度,即可求出时间; (2)要使以C、D、Q、P为顶点的梯形面积等于60cm2,可以分为两种情况,利用梯形面积公式,即(QD+PC)×AB÷2=60,因为Q、P点的速度已知,AD、AB、BC的长度已知,用t可分别表示QD、BC的长,即可求得时间t; (3)使△PQD是等腰三角形,可分三种情况,即PQ=PD、PQ=QD、QD=PD;可利用等腰三角形及直角梯形的性质,分别用t表达等腰三角形的两腰长,再利用两腰相等即可求得时间t. 【解答】解:(1)∵四边形PQDC是平行四边形, ∴DQ=CP, 当P从B运动到C时,如图(1): ∵DQ=AD﹣AQ=16﹣t, CP=21﹣2t ∴16﹣t=21﹣2t 解得t=5 ∴当t=5秒时,四边形PQDC是平行四边形; 四边形PQDC,四个顶点顺序已定,DC不能为对角线; (2)若点P、Q分别沿AD、BC运动时,如图(2): 若点P在线段BC上时, , 即, 解得t=9; 若点P在BC的延长线上时,CP=2t﹣21, 则×12=60 解得t=15. 故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2; (3)当PQ=PD时,如图(3): 作PH⊥AD于H,则HQ=HD ∵QH=HD=QD=(16﹣t) 由AH=BP得2t=(16﹣t)+t, 解得t=秒; 当PQ=QD时QH=AH﹣AQ=BP﹣AQ=2t﹣t=t,QD=16﹣t, ∵QD2=PQ2=t2+122 ∴(16﹣t)2=122+t2 解得t=(秒); 综上可知,当t=秒或t=秒时,△PQD是等腰三角形.查看更多