- 2021-05-06 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上册青岛版数学课件2-4线段的垂直平分线(第1课时)
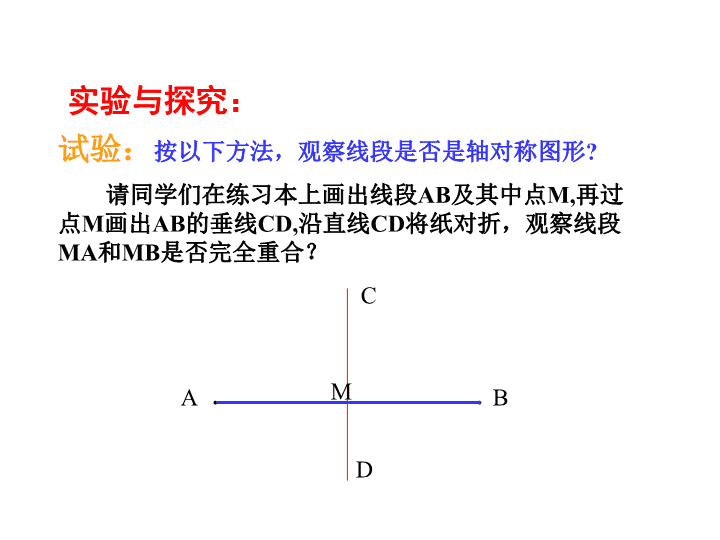
第2章 图形的轴对称 2.4线段的垂直平分线 第1课时 教学目标 1. 运用作图和实验的方法,探索线段的垂直平分线的性质定理和逆定理; 2. 会用尺规作出已知线段的垂直平分线 A C D BM 实验与探究: 试验:按以下方法,观察线段是否是轴对称图形? 请同学们在练习本上画出线段AB及其中点M,再过 点M画出AB的垂线CD,沿直线CD将纸对折,观察线段 MA和MB是否完全重合? 结论:线段MA和MB完全重合,因此,线段AB是轴 对称图形。 A C D BM 问题1:既然线段AB是轴对称图形。那么它的对称 轴是什么呢? (直线CD) 问题2:直线CD具有什么特征或特性? A C D BM (CD⊥AB MA=MB 即:直线CD垂直并 且平分线段AB.) 定义:垂直并且平分一条线段的直线叫做这条线段的垂直平 分线。也称中垂线。 如上图,直线CD就是线段AB的垂直平分线 注意:①线段的中垂线是直线。②直线和射线没有中垂线。 A B 线段的垂直平分线 EA=EB E1 E1A=E1B …… 命题:线段垂直平分线上的 点到这条线段两个端点的距 离相等。 E c D M 动手操作:作线段AB的中垂线CD,垂足 为M;在CD上任取一点E,连结EA、EB; 量一量:EA、EB的长,你能发现什么? 由此你能得到什么规律? A C D BM E 线段垂直平分线的性质: 线段的垂直平分线上的点到这条线段两个端点的 距离相等。 如图: ∵AM=BM,CD⊥AB,E是CD上任意一点(已知), ∴EA=EB(线段垂直平分线上的点到这条线段两 个端点距离相等). 线段的垂直平分线的作法 l已知:线段AB,如图. l求作:线段AB的垂直平分线. l作法: l用尺规作线段的垂直平分线. l1.分别以点A和B为圆心,以大于1/2AB 长为半径作弧,两弧交于点C和D. A B C Dl2. 作直线CD. l则直线CD就是线段AB的垂直平分线. 请你说明CD为什么是AB的垂直平分线,并 与同伴进行交流. 泰安市政府为了方便居民的生活,计划在 三个住宅小区A、B、C之间修建一个购物中 心,试问,该购物中心应建于何处,才能 使 得 它 到 三 个 小 区 的 距 离 相 等 。 A B C 实际问 题 B A C 线段的垂直平分线 1、求作一点P,使 它和△ABC的三个 顶点距离相等. 实际问题 数学化 p PA=PB=PC 应用举例: 2.如图所示,在ΔABC中,边BC的垂直平分线 MN分别交AB于点M,交BC于点N, ΔBMC的周长 为23,且BM=7,求BC的长。 CB M N A查看更多