高中数学 1-3-3 函数的最大(小)值与导数双基限时训练 新人教版选修2-2
【名师一号】2014-2015学年高中数学 1-3-3函数的最大(小)值与导数双基限时训练 新人教版选修2-2
1.函数f(x)=x+2cosx在[0,]上的最大值点为( )
A.x=0 B.x=
C.x= D.x=
解析 令f′(x)=1-2sinx=0,则sinx=,又x∈[0,],∴x=,又f(0)=2,f()=+,f()=,
∴f()最大,∴最大值点为x=.
答案 B
2.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围是( )
A.0≤a<1 B.0
,f(2)=-5<,∴-10,∴当x∈(0,1)时,y′>0;当x∈(1,4)时,y′<0.故当x=1时,y有极大值.又当x=0时,y=0;当x=4时,y=.∴最大值为.
答案 B
6.函数f(x)=sinx+cosx在x∈时,函数的最大值、最小值分别是________.
解析 f′(x)=cosx-sinx,x∈[-,],令f′(x)=0,得x=,又f()=,f(-)=-1,f()=1,即最大值为,最小值为-1.
答案 ,-1
7.函数f(x)=12x-x3在区间[-3,3]上的最小值是________.
解析 f′(x)=12-3x2=3(4-x2),
令f′(x)=0,得x=±2,
而f(-3)=-36+27=-9,
f(-2)=-24+8=-16,
f(2)=24-8=16,
f(3)=36-27=9.
∴最小值是-16.
答案 -16
8.设f(x),g(x)是定义在[a,b]上的可导函数,且f′(x)>g′(x),令F(x)=f(x)-g(x),则F(x)在[a,b]上的最大值为________.
解析 F′(x)=f′(x)-g′(x)>0,
∴F(x)在[a,b]上是增函数.
∴最大值为F(b)=f(b)-g(b).
答案 f(b)-g(b)
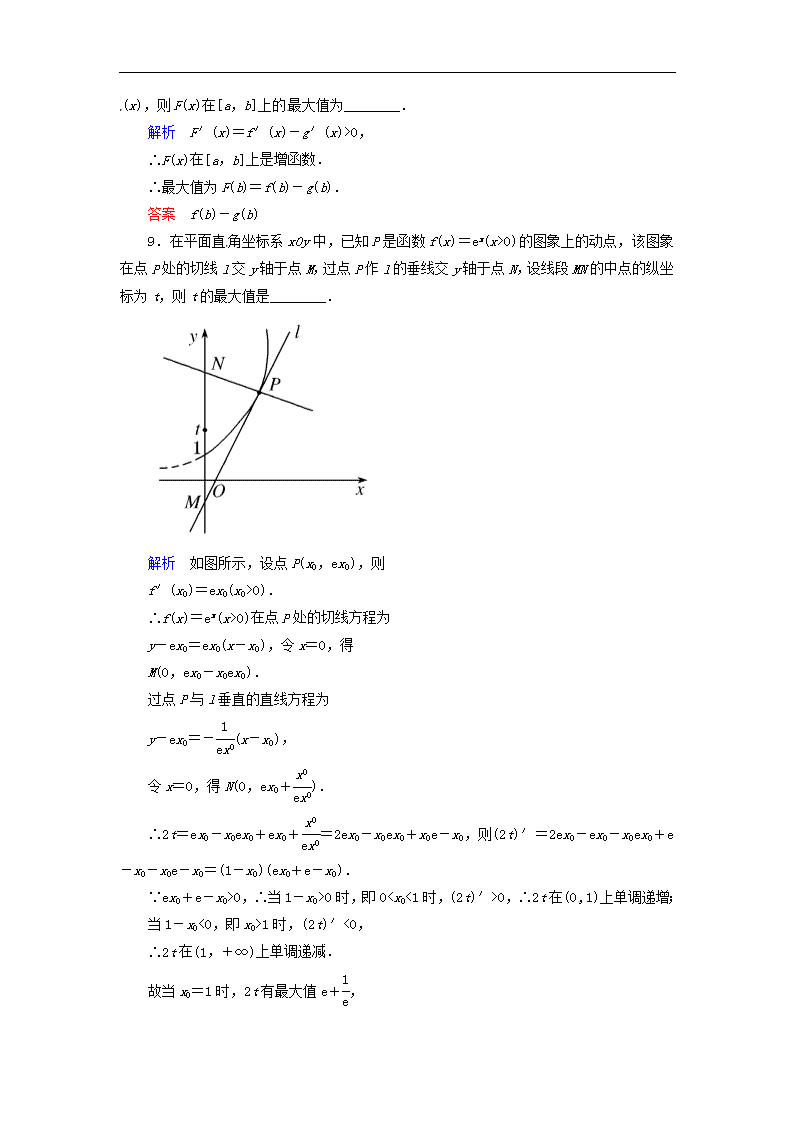
9.在平面直角坐标系xOy中,已知P是函数f(x)=ex(x>0)的图象上的动点,该图象在点P处的切线l交y轴于点M,过点P作l的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是________.
解析 如图所示,设点P(x0,ex0),则
f′(x0)=ex0(x0>0).
∴f(x)=ex(x>0)在点P处的切线方程为
y-ex0=ex0(x-x0),令x=0,得
M(0,ex0-x0ex0).
过点P与l垂直的直线方程为
y-ex0=-(x-x0),
令x=0,得N(0,ex0+).
∴2t=ex0-x0ex0+ex0+=2ex0-x0ex0+x0e-x0,则(2t)′=2ex0-ex0-x0ex0+e-x0-x0e-x0=(1-x0)(ex0+e-x0).
∵ex0+e-x0>0,∴当1-x0>0时,即00,∴2t在(0,1)上单调递增;
当1-x0<0,即x0>1时,(2t)′<0,
∴2t在(1,+∞)上单调递减.
故当x0=1时,2t有最大值e+,
即t的最大值为(e+).
答案 (e+)
10.已知a∈R,f(x)=(x2-4)(x-a).
(1)求f′(x);
(2)若f′(-1)=0,求f(x)在[-2,2]上的最值;
(3)若函数f(x)在(-∞,-2]和[2,+∞)上是递增的,求a的取值范围.
解 (1)由原式得
f(x)=x3-ax2-4x+4a,
∴f′(x)=3x2-2ax-4.
(2)由f′(-1)=0,得a=,
此时f(x)=(x2-4)(x-),
f′(x)=3x2-x-4.
由f′(x)=0,得x=,或x=-1.
又f()=-,f(-1)=,
f(-2)=0,f(2)=0,
∴f(x)在[-2,2]上的最大值为,最小值为-.
(3)f′(x)=3x2-2ax-4的图象是开口向上的抛物线,且过定点(0,-4).
由条件得f′(-2)≥0,f′(2)≥0,
即∴-2≤a≤2.
故a的取值范围是[-2,2].
11.已知a是实数,函数f(x)=x2(x-a).
(1)若f′(1)=3,求a的值及曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[0,2]上的最大值.
解 (1)f′(x)=3x2-2ax,
∵f′(1)=3-2a=3,∴a=0.
又当a=0时,f(1)=1,f′(1)=3,
∴曲线y=f(x)在(1,f(1))处的切线方程为3x-y-2=0.
(2)令f′(x)=0,解得x1=0,x2=.
当≤0,即a≤0时,f(x)在[0,2]上单调递增,从而f(x)max=f(2)=8-4a.
当≥2,即a≥3时,f(x)在[0,2]上单调递减,从而f(x)max=f(0)=0.
当0<<2,即0
查看更多