2018届二轮复习（理）层级二保分专题(六)　点、直线、平面之间的位置关系课件（全国通用）

2018届二轮复习（理）层级二保分专题(六)　点、直线、平面之间的位置关系课件（全国通用）

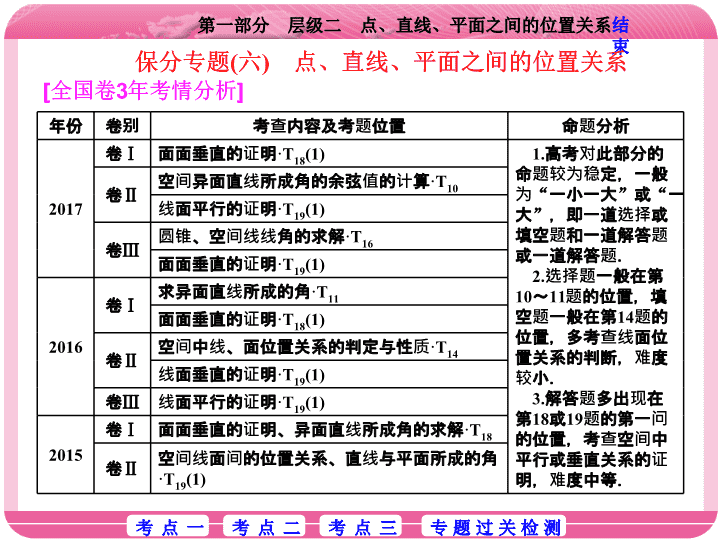
年份 卷别 考查内容及考题位置 命题分析 2017 卷 Ⅰ 面面垂直的证明 ·T 18 (1) 1. 高考对此部分的命题较为稳定，一般为 “ 一小一大 ” 或 “ 一大 ” ，即一道选择或填空题和一道解答题或一道解答题． 2 . 选择题一般在第 10 ～ 11 题的位置，填空题一般在第 14 题的位置，多考查线面位置关系的判断，难度较小． 3 . 解答题多出现在第 18 或 19 题的第一问的位置，考查空间中平行或垂直关系的证明，难度中等． 卷 Ⅱ 空间异面直线所成角的余弦值的计算 ·T 10 线面平行的证明 ·T 19 (1) 卷 Ⅲ 圆锥、空间线线角的求解 ·T 16 面面垂直的证明 ·T 19 (1) 2016 卷 Ⅰ 求异面直线所成的角 ·T 11 面面垂直的证明 ·T 18 (1) 卷 Ⅱ 空间中线、面位置关系的判定与性质 ·T 14 线面垂直的证明 ·T 19 (1) 卷 Ⅲ 线面平行的证明 ·T 19 (1) 2015 卷 Ⅰ 面面垂直的证明、异面直线所成角的求解 ·T 18 卷 Ⅱ 空间线面间的位置关系、直线与平面所成的角 ·T 19 (1) 线面平行的性质定理，线面平行，则线线平行，可得 PA ∥ DE 信息 ⑤ ： PA ∥ 平面 BDE 面面垂直的判定定理，线线垂直 ⇒ 线面垂直 ⇒ 面面垂直 信息 ④ ：平面 BDE ⊥ 平面 PAC 证明线线垂直，可转化到证明一直线垂直于另一直线所在平面，再由线面垂直的定义可得 信息 ③ ： PA ⊥ BD 等腰三角形中线与高线合一，可得 BD ⊥ AC 信息 ② ： AB ＝ BC ， D 为 AC 的中点 (1) 证明线面平行的条件：一直线在平面外，一直线在平面内 (2) 证明线面垂直时的条件：直线垂直于平面内两条相交直线 (3) 求点到面的距离时要想到借助锥体的 “ 等体积性 ” 线面垂直的判定定理，可证 PA ⊥ 平面 ABC 信息 ① ： PA ⊥ AB ， PA ⊥ BC 注意什么 想到什么 有什么 “专题过关检测”见“ 专题检测 ( 十四 )” ( 单击进入电子文档 )