- 2021-05-06 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
西藏自治区日喀则市南木林高级中学2020届高三毕业班第六次月考数学试题
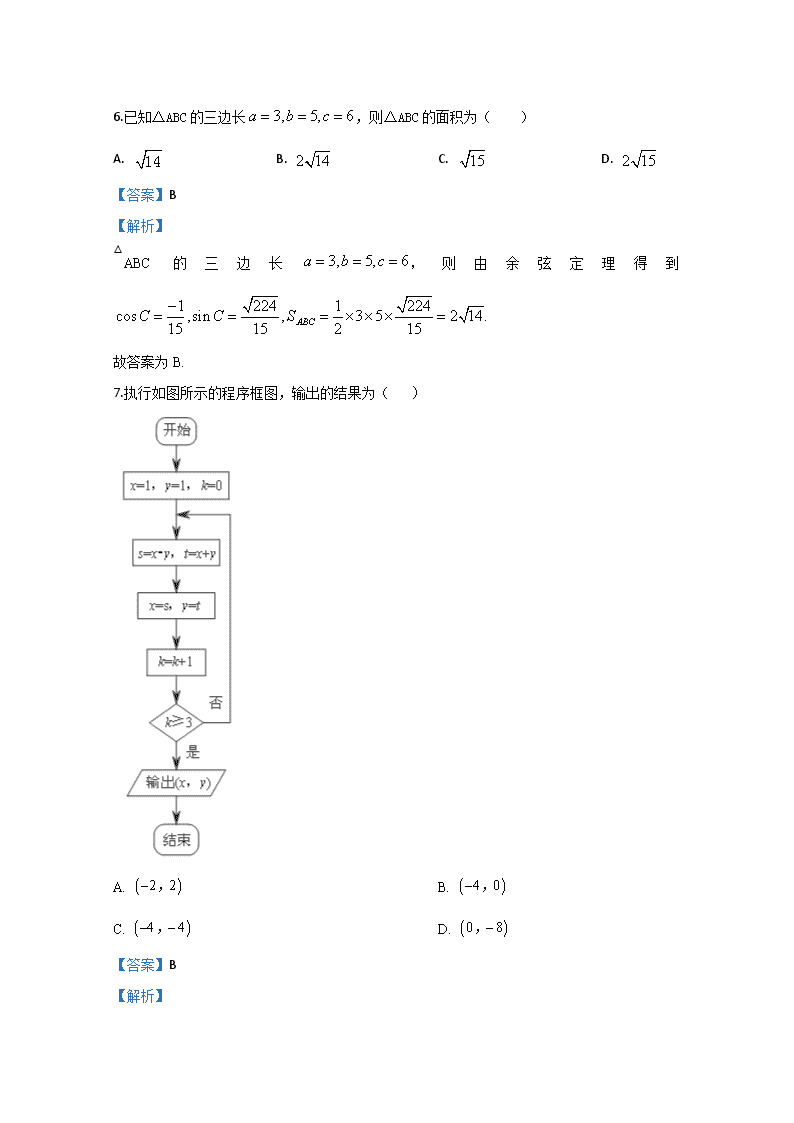
数学试卷 一、选择题: 1.若集合,集合,则等于( ) A. B. C. D. 【答案】B 【解析】 集合,集合,所以 .故选B. 2.若复数满足,则( ) A. 1 B. C. 2 D. 【答案】B 【解析】 试题分析:,故. 考点:复数的模. 3. 某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则从高二年级抽取的学生人数为( ) A. 15 B. 20 C. 25 D. 30 【答案】A 【解析】 试题分析:由分层抽样得,从高二年级抽取的学生人数为人. 考点:分层抽样. 4.如图,在矩形ABCD中,AB=,BC=2,点E为BC的中点,点F在边CD上,若,则的值是( ) A. 2﹣ B. 1 C. D. 2 【答案】C 【解析】 分析:根据所给的图形,把已知向量用矩形的边所在的向量来表示,做出要用的向量的模长,表示出要求得向量的数量积,注意应用垂直的向量数量积等于0,得到结果. 详解:∵, ∴||=1,||=﹣1, 故答案为 C. 点睛:(1)向量的运算将向量与代数有机结合起来,这就为向量和函数的结合提供了前提,运用向量的有关知识可以解决某些函数问题;(2)以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的运算,将问题转化为解不等式或求函数值域,是解决这类问题的一般方法;(3)向量的两个作用:①载体作用:关键是利用向量的意义、作用脱去“向量外衣”,转化为我们熟悉的数学问题;②工具作用:利用向量可解决一些垂直、平行、夹角与距离问题. 5.在等差数列中,则( ) A. B. C. D. 【答案】B 【解析】 试题分析:依题意,有,解得. 考点:等差数列. 6.已知△ABC的三边长,则△ABC的面积为( ) A. B. C. D. 【答案】B 【解析】 △ABC的三边长,则由余弦定理得到 故答案为B. 7.执行如图所示的程序框图,输出的结果为( ) A. B. C. D. 【答案】B 【解析】 试题分析:程序执行中的数据变化如下:成立,输出 考点:程序框图 8.某三棱锥的三视图如图所示,则该三棱锥的表面积是( ) A. B. C. D. 5 【答案】C 【解析】 分析】 根据三视图还原几何体,可得该棱锥4个面中有2个为直角三角形,2个面是等腰三角形,利用三视图中的数据即可得结果. 【详解】 该几何体是棱长分别为 的长方体中的三棱锥: , 其中: , 该几何体的表面积为: . 故选C. 【点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响. . 9.已知,则( ) A. B. C. D. 【答案】D 【解析】 试题分析:,选D. 考点:同角三角函数关系 【方法点睛】三角函数求值的三种类型 (1)给角求值:关键是正确选用公式,以便把非特殊角的三角函数转化为特殊角的三角函数. (2)给值求值:关键是找出已知式与待求式之间的联系及函数的差异. ①一般可以适当变换已知式,求得另外函数式的值,以备应用; ②变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的. (3)给值求角:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,确定角. 10.已知函数,则的值为( ) A. B. C. D. 【答案】B 【解析】 试题分析:由于,,,即, ,故答案为B. 考点:分段函数的应用. 11.已知圆:,点,若上存在两点,满足,则实数的取值范围是( ) A. B. C. D. 【答案】C 【解析】 【分析】 ,则为中点,由几何法可得,求出的范围,即可求出的范围 【详解】因为点满足,为中点, 设圆心到直线的距离为,则有, ,因为 , , 故选:C 【点睛】直线与圆位置关系问题的求解策略 (1)判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,则用几何法;若方程中含有参数,或圆心到直线的距离的表达式较繁琐,则用代数法.能用几何法,尽量不用代数法. (2)已知直线与圆的位置关系求参数的取值范围时,可根据数形结合思想利用直线与圆的位置关系的判断条件建立不等式进行解决. 12.已知函数与满足:,且在区间 上为减函数,令,则下列不等式正确的是( ) A B. C. D. 【答案】B 【解析】 试题分析:关于对称,在区间上为减函数,所以在区间上为增函数,而, 所以,,选B. 考点:函数性质综合应用 二、填空题: 13.设向量,,,则______. 【答案】 【解析】 【分析】 由向量数量积坐标公式计算可得 【详解】因向量,, ,, 故答案为: 【点睛】本题考查平面向量数量积的运算. 平面向量数量积的运算常见思路与方法: 根据定义计算数量积的思路:根据图形之间的关系,用长度和相互之间的夹角都已知的向量分别表示出要求数量积的两个向量,然后再根据平面向量数量积的定义和性质进行计算求解. 利用坐标计算数量积的方法:先根据共线、垂直等条件计算出这两个向量的坐标,求解过程要注意方程思想的应用;再根据数量积的坐标公式进行运算即可. 14.经过圆:的圆心,且与直线垂直的直线方程是______. 【答案】 【解析】 【分析】 求出圆心坐标,所求直线与垂直,则 ,点斜式写出直线方程. 【详解】因为所求直线与垂直,则,又圆心坐标 所以直线方程为: 即 故答案为: 【点睛】(1)在求直线方程时,应选择适当的形式,并注意各种形式的适用条件. (2)对于点斜式、截距式方程使用时要注意分类讨论思想的运用(若采用点斜式,应先考虑斜率不存在的情况;若采用截距式,应先判断截距是否为零). 15.(理科)二项式的展开式中常数项为14,则______. 【答案】2 【解析】 【分析】 写出二项式的展开式公式,利用常数项为14,求出参数 【详解】二项式的展开式通项公式为 命令,则 , 故答案为:2 【点睛】二项展开式问题的常见类型及解法 (1)求展开式中的特定项或其系数.可依据条件写出第项,再由特定项的特点求出值即可. (2)已知展开式的某项或其系数求参数.可由某项得出参数项,再由通项公式写出第项,由特定项得出值,最后求出其参数. 16.已知实数满足,则目标函数的最大值是________________. 【答案】5. 【解析】 由约束条件作出可行域如图, 联立. 化目标函数z=2x﹣y为y=2x﹣z,由图可知,当直线y=2x﹣z过A时, 直线在y轴上的截距最小,z有最大值为5. 故答案为5. 17.若f(x)=2x+a×2﹣x为奇函数,则a= . 【答案】 【解析】 试题分析:因为为奇函数,故,得到关于的方程,解方程得. 考点:函数的奇偶性. 【方法点睛】如果对于函数定义域内的任意一个,都有,那么函数就叫做奇函数,反过来如果一个为奇函数,那么对于函数定义域内的任意一个,也都有成立.利用这个性质可以建立关于的方程,解方程即可.特别的如果奇函数定义域中有的话,必有.还可以利用这个性质来解决这个问题,使得计算过程更简单. 三、解答题: 18.各项均为正数的等比数列中,,且成等差数列. (Ⅰ)求数列的通项公式; (Ⅱ)数列,已知,求的前项和. 【答案】(Ⅰ);(Ⅱ) . 【解析】 试题分析:(1)根据题意得到解得:或舍去负值,故得到数列的通项;(2)根据第一问得到,裂项求和即可. 解析: (Ⅰ) ,,成等差数列, 2=+即: 解得:或(舍) . (Ⅱ)由(Ⅰ)可得: 19.的内角A,B,C的对边分别为a,b,c.已知. (1)求角C;(2)若,,求的周长. 【答案】(1)(2) 【解析】 【详解】试题分析:(1)根据正弦定理把化成,利用和角公式可得从而求得角;(2)根据三角形的面积和角的值求得,由余弦定理求得边得到的周长. 试题解析:(1)由已知可得 (2) 又 , 的周长为 考点:正余弦定理解三角形. 20.某医院对治疗支气管肺炎的两种方案,进行比较研究,将志愿者分为两组,分别采用方案和方案进行治疗,统计结果如下: 有效 无效 合计 使用方案组 96 120 使用方案组 72 合计 32 (1)完成上述列联表,并比较两种治疗方案有效的频率; (2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关? 附:,其中. 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 【答案】(1)列联表见解析,使用方案治疗有效的频率更高些;(2)不能. 【解析】 【分析】 (1)由游客购买情况统计人数分布表数据直接填入列联表, (2)代入公式,计算出的值,与独立性检验判断表比较作出判断. 【详解】(1) 根据题意,填表如下: 有效 无效 合计 使用方案组 96 24 120 使用方案组 72 8 80 合计 168 32 200 使用方案有效的频率, 使用方案有效的频率, ∴使用方案治疗有效的频率更高些. (2), ∴不能在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关. 【点睛】本题考查独立性检验. 独立性检验的关键是正确列出2×2列联表,并计算出的值;独立性检验是对两个变量有关系的可信程度的判断,而不是对它们是否有关系的判断. 21.已知是椭圆C:上一点,点P到椭圆C两个焦点的距离之和为. (Ⅰ)求椭圆C的方程; (Ⅱ)设A,B是椭圆C上异于点P的两点,直线PA与直线交于点M, 是否存在点A,使得?若存在,求出点A的坐标;若不存在,请说明理由. 【答案】(Ⅰ);(Ⅱ)存在点A(,),使得. 【解析】 试题分析:(Ⅰ)椭圆过点P(0,1)可得b=1,由点P到两焦点距离和为,可得,进而可得结果;(Ⅱ)设,依题意得:直线的斜率存在, 则直线的方程为: ,又等价于且点A在y轴的右侧, 从而, 从而可得结果. . 试题解析: (Ⅰ)由椭圆C:过点P(0,1)可得b=1, 又点P到两焦点距离和为,可得, 所以椭圆C的方程. (Ⅱ)设A(m,n),依题意得:直线PA的斜率存在, 则直线PA的方程为: , 令x=4,,即M, 又等价于且点A在y轴的右侧, 从而, 因为点A在y轴的右侧, 所以 , 解得 , 由点A在椭圆上,解得:, 于是存在点A(,),使得. 【方法点晴】本题主要考查待定系数法求椭圆标准方程以及解析几何中的存在性问题,属于难题.解决存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在,注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规方法题很难时采取另外的途径. 22.设函数,曲线在点处的斜率为0. (Ⅰ)求的值; (Ⅱ)求证:当时,. 【答案】(Ⅰ);(Ⅱ)见解析. 【解析】 试题分析:(1)根据导数的几何意义得到;(2)只需证:,令 ,求导研究单调性,得到函数最小值大于0即可. 解析: (Ⅰ) 由题意可得: (Ⅱ)只需证:,令 由解得:在递减,在上递增, 故 由可知:在上递增, 故 故 即:. 点睛:利用导数证明不等式常见类型及解题策略(1) 构造差函数.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数. 请考生在22,23,二题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑. 极坐标与参数方程选讲 23.在平面直角坐标系xOy中,曲线C的参数方程为,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系. (1)求曲线C的极坐标方程; (2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值. 【答案】(1)ρ2﹣6ρcosθ﹣8ρsinθ+21=0.(2)9﹣2. 【解析】 【分析】 (1)先将化简成直角坐标方程,再利用与化简即可. (2)由为以为底,到的距离为高可知要求面积的最小值即求到 的距离最大值.再设求解最值即可. 【详解】(1)∵曲线C的参数方程为,(θ为参数),有. 上下平方相加得曲线C的直角坐标方程为, 化简得 将与,代入得曲线C的直角坐标方程有: . (2)设点到直线AB:x+y+2=0的距离为d, 则, 当sin()=﹣1时,d有最小值, 所以△ABM面积的最小值S9﹣2. 【点睛】本题主要考查了参数方程与直角坐标和极坐标系的互化,同时与考查了圆上的点到直线距离最值的问题,属于中等题型. 选修4-5:不等式选讲 24.选修4-5:不等式选讲 已知函数. (Ⅰ)当时,求不等式的解集; (Ⅱ)对于任意实数,不等式恒成立,求的取值范围. 【答案】(1);(2). 【解析】 试题分析:(1)将代入 ,去掉绝对值符号,即可求出不等式的解集. (2)根据题意得.由 ,,,即可求出的取值范围. 试题解析:(Ⅰ),. 当时,由或,得 ∴不等式的解集为. (Ⅱ)不等式对任意的实数恒成立,等价于对任意的实数,恒成立,即 ∵ ∴又,所以,.查看更多