- 2021-04-29 发布 |
- 37.5 KB |
- 18页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年安徽省滁州市定远县西片三校高二上学期期末考试数学(文)试题 Word版
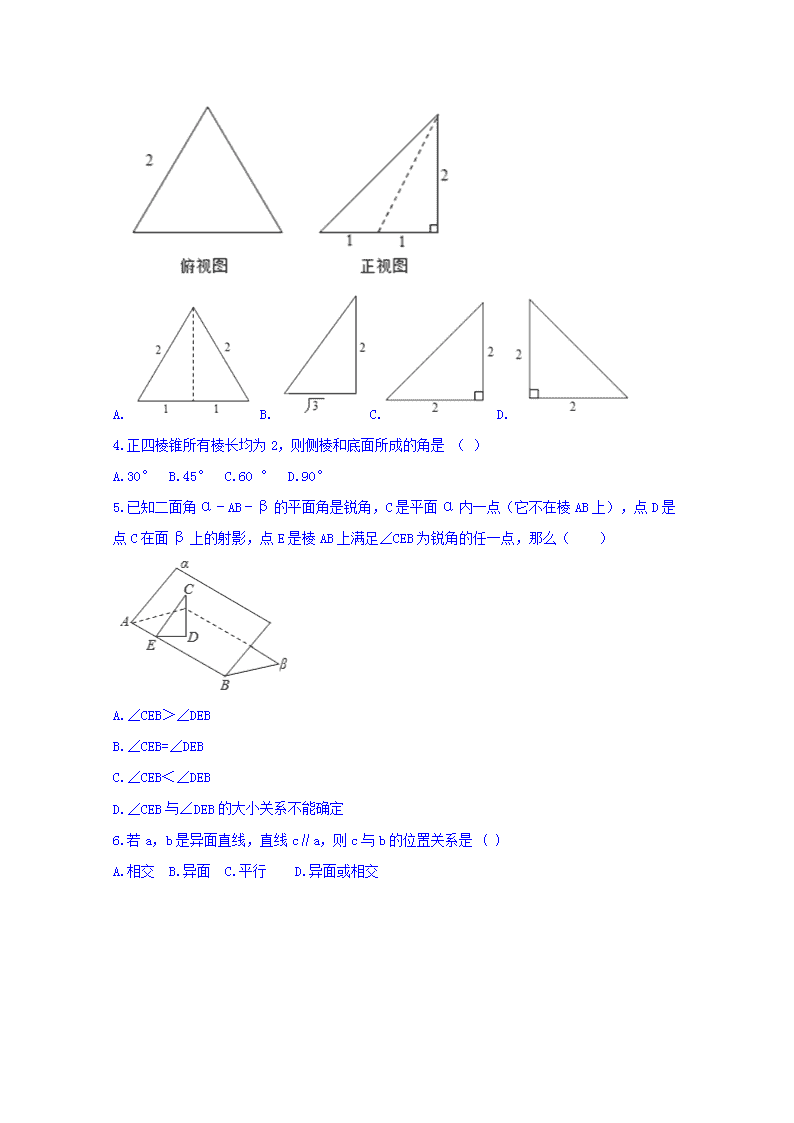
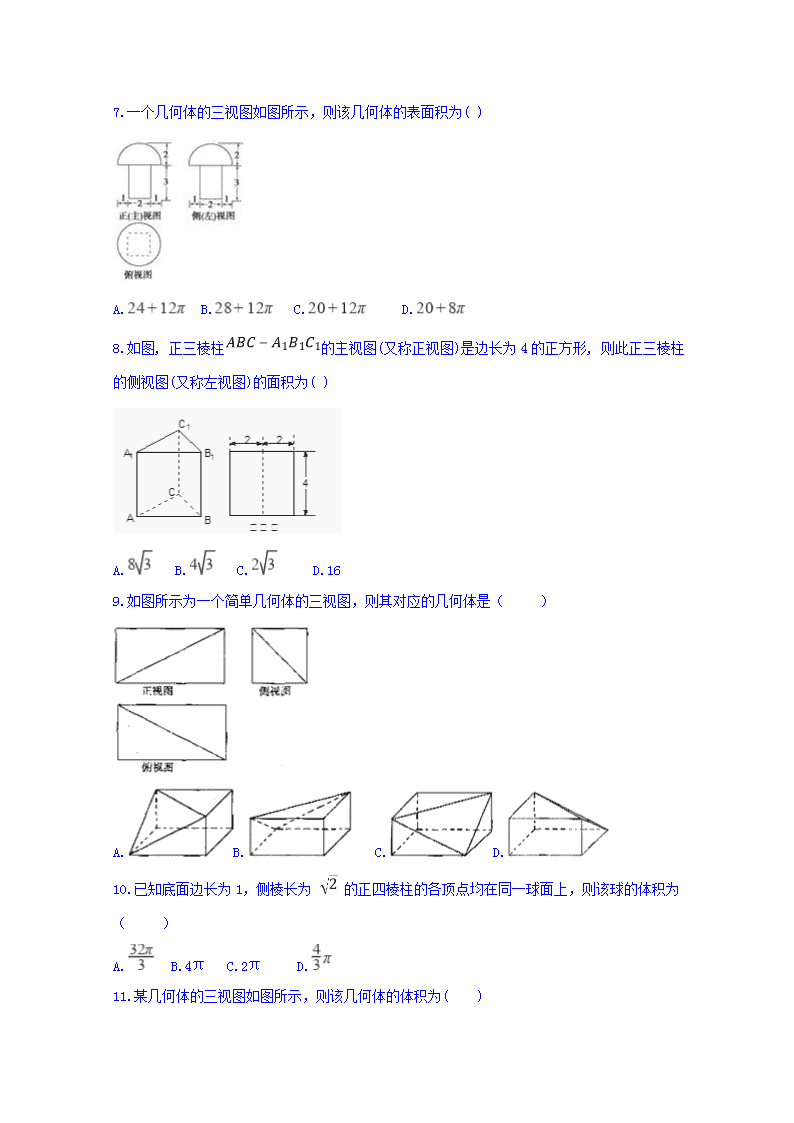
定远县西片三校2017-2018学年上学期期末考试 高二(文科)数学 2018.2 考生注意: 1、本卷满分150分,考试时间120分钟; 2、答题前请在答题卷上填写好自己的学校、姓名、班级、考号等信息; 3、请将答案正确填写在答题卷指定的位置,在非答题区位置作答无效。 一、选择题 1.已知表示空间一条直线,表示空间两个不重合的平面,有以下三个语句:①;②;③.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( ) A.0 B.1 C.2 D.3 2.一个体积为的正三棱柱的三视图,如图所示,则此正三棱柱的侧视图面积为( ) A.12 B. C.8 D. 3.已知三棱锥的正视图与俯视图如图,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( ) A.B.C.D. 4.正四棱锥所有棱长均为2,则侧棱和底面所成的角是 ( ) A.30° B.45° C.60 ° D.90° 5.已知二面角α﹣AB﹣β的平面角是锐角,C是平面α内一点(它不在棱AB上),点D是点C在面β上的射影,点E是棱AB上满足∠CEB为锐角的任一点,那么( ) A.∠CEB>∠DEB B.∠CEB=∠DEB C.∠CEB<∠DEB D.∠CEB与∠DEB的大小关系不能确定 6.若a,b是异面直线,直线c∥a,则c与b的位置关系是 ( ) A.相交 B.异面 C.平行 D.异面或相交 7.一个几何体的三视图如图所示,则该几何体的表面积为( ) A. B. C. D. 8.如图, 正三棱柱的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( ) A. B. C. D.16 9.如图所示为一个简单几何体的三视图,则其对应的几何体是( ) A.B. C.D. 10.已知底面边长为1,侧棱长为 的正四棱柱的各顶点均在同一球面上,则该球的体积为( ) A. B.4π C.2π D. 11.某几何体的三视图如图所示,则该几何体的体积为( ) A. B. C. D. 12.在等腰Rt△ABC中,AB=BC=1,M为AC的中点,沿BM把它折成二面角,折后A与C的距离为1,则二面角C-BM-A的大小为( ) A. 30° B. 60° C. 90° D. 120° 第II卷(非选择题) 二、填空题 13.如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1 , B1C1的中点,P是上底面的棱AD上的一点,AP= ,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 14.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为 . 15.要做一个无盖型容器,将长为15cm,宽为8cm的长方形铁皮先在四角分别截去一个相同的小正方形后再进行焊接,当该容器容积最大时高为 cm. 16.如图是正方体的平面展开图,则在这个正方体中,以下四个判断中,正确的序号是_________. ①与平行;②与是异面直线;③与成60°角;④与是异面直线. 三、解答题 17.如图,三棱柱ABC﹣A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C. (I)求证:平面AA1B1B⊥平面BB1C1C; (II)求二面角B﹣AC﹣A1的余弦值. 18.如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD. (1)求证:平面PBC⊥平面PAD;(2)若PA=1,求四棱锥P﹣ABCD的体积. 19.如图,在底面是直角梯形的四棱锥S﹣ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD= . (Ⅰ )求四棱锥S﹣ABCD的体积; (Ⅱ)求面SCD与面SBA所成的二面角的正切值. 20.如图,平面为圆锥的轴截面, 为底面圆的圆心, 为母线的中点, 为底面圆周上的一点, 求该圆锥的侧面积; 若直线与所成的角为,求的长. 21.如图,三棱锥中,平面平面, ,点在线段上,且, ,点在线段上,且平面. (1)证明: ; (2)证明: 平面; (3)若四棱锥的体积为7,求线段的长. 22.如下图,在几何体中, ,且是正三角形,四边形为正方形, 是线段的中点, , (Ⅰ)若是线段上的中点,求证: (Ⅱ)若是线段上的动点,求三棱锥的体积 参考答案 1.B 【解析】命题①:若 , 则是正确的命题,如图(1)过直线作一个平面 , , 则由 , 结合线面平行的性质可知 , 因为 , 所以 , 而 , 所以由面面垂直的判定可得;命题②:若 , 则是错误的命题,如图(2),直线可能在平面内;命题③:若 , 则是错误的命题,如图(3),直线可能在内,如图(4),直线也可能与平行,综上可知,三个命题中只有一个命题是正确的,故选B. 2.D 【解析】此几何体是一个正三棱柱,正视图即内侧面,底面正三角形的高是 2 , 由正三角形的性质可以求出其边长,由于本题中体积已知,故可设出棱柱的高,利用体积公式建立起关于高的方程求高,再由正方形的面积公式求侧视图的面积即可.设棱柱的高为h,由左视图知,底面正三角形的高是 2 , 由正三角形的性质知,其边长是4,故底面三角形的面积是×2× 4="4" 由于其体积为 12 , 故有h×4=12 , 得h=3,由三视图的定义知,侧视图的宽即此三棱柱的高,故侧视图的宽是3,其面积为3×2=6 , 故选D 3.B 【解析】由俯视图可知三棱锥的底面是个边长为2的正三角形, 由正视图可知三棱锥的一条侧棱垂直于底面,且其长度为2 故其侧视图为直角边长为2和的直角三角形, 故选B. 4.B 【解析】先做出要求的线面角,把它放到一个直角三角形中,利用直角三角形中的边角关系求出此角. 如图, 四棱锥P-ABCD中,过P作PO⊥平面ABCD于O,连接AO, 则AO是AP在底面ABCD上的射影.∴∠PAO即为所求线面角, ∵AO= , PA=2, ∴cos∠PAO== . ∴∠PAO=45°,即所求线面角为45°. 故选 B. 5.A 【解析】过C向AB做垂线交AB于F,连接DF,因为CD⊥AB又CF⊥AB, 所以AB⊥面CDF,所以CF垂直于AB 在直角三角形CDF中,CF为斜边DF为直角边,所以CF>DF 易知tan∠CEF=tan∠DEB= 由CF>DF知,∠CEB>∠ DEB 故选A. 6.D 【解析】若a,b是异面直线,直线c∥a,所以c与b可能异面,可能相交. 由a、b是异面直线,直线c∥a知c与b的位置关系是异面或相交, 故选D. 7.A 【解析】由三视图可知直观图上半部分为半球,半径为2,下半部分为长方体,三边为2,2,3所以表面积为,选A。 8.A 【解析】由主视图可知正三棱柱底面边长为4,侧棱长为4,所以左视图为矩形,两边分别为4和,其面积为 9.A 【解析】对于A,该几何体的三视图恰好与已知图形相符,故A符合题意; 对于B,该几何体的正视图的矩形中,对角线应该是虚线,故不符合题意; 对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意; 对于D,该几何体的侧视图的矩形中,对角线应该是虚线,不符合题意 故选:A 10.D 【解析】:∵正四棱柱的底面边长为1,侧棱长为 , ∴正四棱柱体对角线的长为 =2 又∵正四棱柱的顶点在同一球面上, ∴ 正四棱柱体对角线恰好是球的一条直径,得球半径R=1 根据球的体积公式,得此球的体积为V= πR3= π. 故选:D. 11.C 【解析】由三视图可知,该几何体为直三棱柱, 其体积为 故选:C 12.C 【解析】.如图,由A′B=BC=1,∠A′BC=90°知A′C=. ∵M为A′C的中点,∴MC=AM=,且CM⊥BM,AM⊥BM, ∴∠CMA为二面角C-BM-A的平面角. ∵AC=1,MC=MA=,∴MC2+MA2=AC2, ∴∠CMA=90°,故选C. 13. a 【解析】∵平面ABCD∥平面A1B1C1D1 , MN⊂平面ABCD ∴MN∥平面A1B1C1D1 , 又PQ=面PMN∩平面A1B1C1D1 , ∴MN∥PQ. ∵M、N分别是A1B1、B1C1的中点 ∴MN∥A1C1∥AC, ∴PQ∥AC,又AP= ,ABCD﹣A1B1C1D1是棱长为a的正方体, ∴CQ= ,从而DP=DQ= , ∴PQ= = = a. 故答案为: a 14. 【解析】如图所示,取B1C1的中点F,连接EF, ED1 , ∴CC1∥EF, 又EF⊂平面D1EF,CC1⊄平面D1EF, ∴CC1∥平面D1EF. ∴直线C1C上任一点到平面D1EF的距离是两条异面直线D1E与CC1的距离. 过点C1作C1M⊥D1F, ∵平面D1EF⊥平面A1B1C1D1 . ∴C1M⊥平面D1EF. 过点M作MP∥EF交D1E于点P,则MP∥C1C. 取C1N=MP,连接PN,则四边形MPNC1是矩形. 可得NP⊥平面D1EF, 在Rt△D1C1F中,C1M•D1F=D1C1•C1F,得 = . ∴点P到直线CC1的距离的最小值为 . 故答案为 15. 【解析】设容器的高为x,(0<x<4), 则当该容器容积V=(15﹣2x)(8﹣2x)x=4x3﹣46x2+120x, V′=12x2﹣92x+120, 由V′=0,得x= 或x=6(舍), ∵x∈(0, )时,V′>0;x∈( ,4)时,V′<0. ∴当x= cm时,该容器容积最大. 故答案为: . 16.③④ 【解析】 展开图还原的正方体如图,不难看出,①与平行;错误的,应为异面直线;②与是异面直线,错误;应是平行线;③与成,是正确的;④与是异面直线,是正确的,故选③④. 17.证明:(Ⅰ)由侧面AA1B1B为正方形,知AB⊥BB1 . 又AB⊥B1C,BB1∩B1C=B1 , ∴AB⊥平面BB1C1C, 又AB⊂平面AA1B1B,∴平面AA1B1B⊥BB1C1C. (Ⅱ)由题意, CB=CB1 , 设O是BB1的中点,连接CO,则CO⊥BB1 . 由(Ⅰ)知,CO⊥平面AB1B1A.建立如图所示的坐标系O﹣xyz. 其中O是BB1的中点,Ox∥AB,OB1为y轴,OC为z轴. 不妨设AB=2,则A(2,﹣1,0),B(0,﹣1,0),C(0,0,),A1(2,1,0). =(﹣2,0,0),=(﹣2,1,),=(0,2,0). 设=(x1 , y1 , z1)为面ABC的法向量,则•=0,•=0, 即取z1=﹣1,得=(0,,﹣1). 设=(x2 , y2 , z2)为面ACA1的法向量,则•=0,•=0, 即取x2=,得=(,0,2). 所以cos〈n1 , n2>==﹣. 因此二面角B﹣AC﹣A1的余弦值为﹣. 18.(1)证明:(1)∵AD⊥⊙O所在的平面PAB,PB⊂⊙O所在的平面PAB, ∴AD⊥PB, ∵PA⊥PB,PA∩AD=A, ∴PB⊥平面PAD, ∵PB⊂平面PBC, ∴平面PBC⊥平面PAD; (2)解:在平面PAB内过P作PE⊥AB于E, ∵AD⊥⊙O所在的平面PAB,PE⊂⊙O所在的平面PAB, ∴AD⊥PE, ∵AD∩AB=A, ∴PE⊥平面ABCD, 直角△PAB中,AB=2,PA=1, ∴PB=, ∴PE==, ∴四棱锥P﹣ABCD的体积V=. 19.(Ⅰ)直角梯形ABCD的面积是M底面=(BC+AD)xAB= ∴四棱锥S﹣ABCD的体积是V=xSAxM底面=x1x=; (Ⅱ)延长BA、CD相交于点E,连接SE, 则SE是所求二面角的棱 ∵AD∥BC,BC=2AD ∴EA=AB=SA, ∴SE⊥SB ∵SA⊥面ABCD,得面SEB⊥面EBC, EB是交线.又BC⊥EB, ∴BC⊥面SEB, 故SB是SC在面SEB上的射影, ∴CS⊥SE, 所以∠BSC是所求二面角的平面角 ∵SB==,BC=1,BCSB ∴tan∠BSC= 即所求二面角的正切值为. 20.(1) (2) (1)由题意知, 平面, 在中, 该圆锥的侧面积; 取的中点,连接 为母线的中点, 为的中位线, 平面平面 平面 直线与所成的角为, 在中, 21.(Ⅰ)证明过程见解析;(Ⅱ)证明过程见解析;(Ⅲ) 或. (Ⅰ)证明: //平面. 平面,平面平面, 所以根据线面平行的性质可知// , (Ⅱ)由可知为等腰中边的中点,故, 又平面平面,平面平面 , 平面 , , 平面, 平面, 又, // 所以平面. (Ⅲ)设,在直角三角形中, , ,即, // 知相似于,所以, 由得, 从而四边形的面积为, 由(Ⅱ)可知是四棱锥的高, , 所以, 所以,所以或, 所以或. 22.(1)详见解析;(2). (Ⅰ)解法一:取的中点,连接, 是线段的中点, 且, 四边形为正方形, 是线段上的中点 且, ∴且, 四边形是平行四边形, , , 。 解法二:取的中点,连接, 是线段的中点, 四边形为正方形, , , , 。 又是线段上的中点, , , 。 , , , (Ⅱ)四边形为正方形, , , , =查看更多