解直角三角形及其应用导学案

解直角三角形及其应用导学案

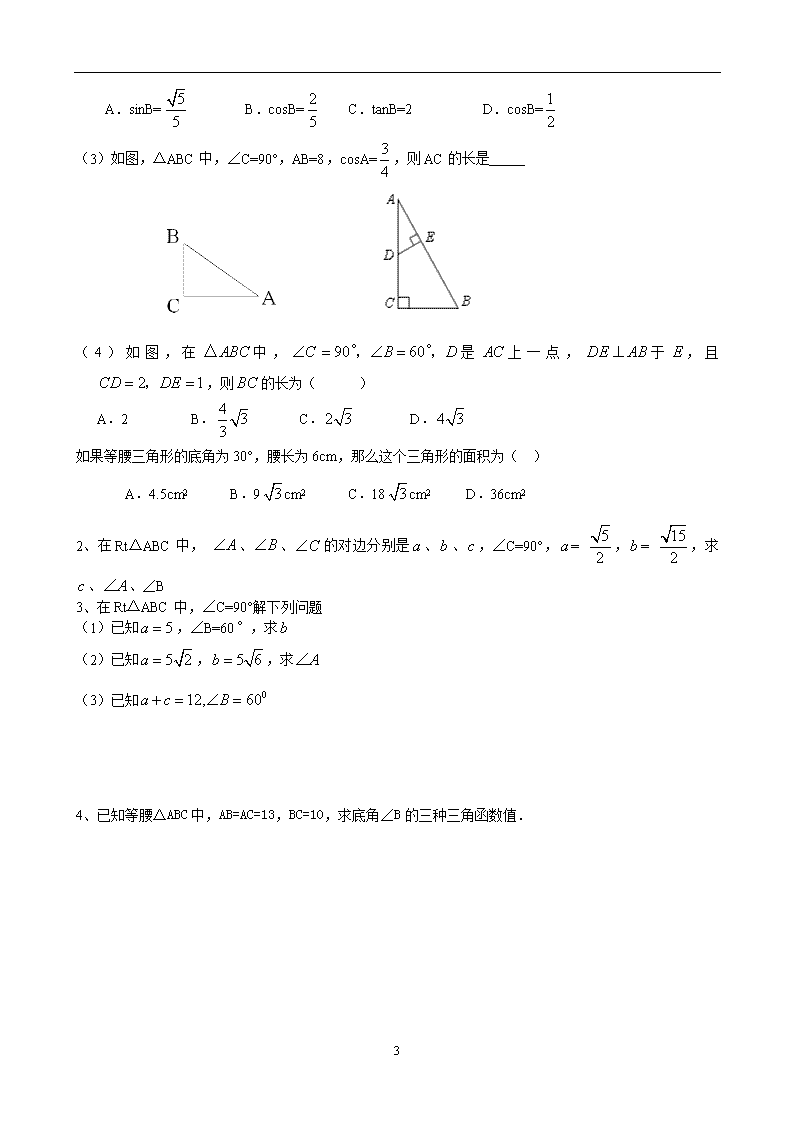
‎4.3解直角三角形及其应用（第1课时）导学案 ‎ 学习目标：‎ ‎1、使学生了解解直角三角形的概念，能运用直角三角形的角与角(两锐角互余)，边与边(勾股定理)、边与角关系解直角三角形。（重点）‎ ‎2、渗透数形结合的数学思想，培养学生良好的学习习惯。‎ 难点：三角函数在解直角三角形中的灵活运用。‎ 学习过程 一、创设情境 问题：如图，我军某部在一次野外训练中，有一辆坦克准备通过一座小山，已知山脚和山顶的水平距离为1000米，山高为565米．如果这辆坦克能够爬的斜坡，试问：它能不能通过这座小山?（提示：求出的大小，再与比较）‎ 学了这节内容，问题就迎刃而解了。这节课我们一起来学习4.3解直角三角形及其应用。‎ 二、快乐自学，阅读课本，回答下列问题。‎ ‎1、直角三角形的元素：我们把直角三角形的两个锐角及三条边叫做直角三角形的五大元素。‎ ‎2、直角三角形ABC中，，这五个元素间有哪些等量关系呢？‎ ‎（1）锐角之间关系 ‎（2）三边之间关系 ‎（3）边角之间关系 ‎3、自学检测 ‎（1）在直角三角形中， ，叫作解直角三角形。‎ ‎（2）在Rt△ABC中，∠C=90°，AB=5，BC=3，则cosA=________．‎ ‎（3）在Rt△ABC中， 、、的对边分别是、、，∠C=90°，∠B=60°，=4，则=________，=________，=________。‎ 二、合作探究 ‎1、探索解直角三角形至少需要多少元素？完成课本做一做和动脑筋。‎ ‎（1）给你一条边你能把剩余的元素都求出来吗？为什么？‎ ‎（2）给你一个锐角你能把剩余的元素都求出来吗？为什么？‎ ‎（3）给你两个角你能把剩余的元素求出来吗？为什么？‎ ‎（4）给你两条边你能把剩余的元素都求出来吗？怎样求（请画出图形分类说明了）‎ ‎（5）给你一条边和一个锐角你能把剩余的元素都求出来吗？怎样求？请画出图形分类说明，关键在哪里？‎ 3‎ ‎（6）通过前面的分析请你总结出：解直角三角形必备的条件： ‎ ‎2、解直角三角形的应用 例1、在Rt△ABC中，∠C＝90°，∠A＝30°，a=5，解直角三角形。‎ 例2、已知：在Rt△ABC中，∠C＝90°，=45.60cm,b=8.5cm，求 、∠A、∠B 归纳解直角三角形的两种型 三、应用提高 例3：如图，在△ABC中，∠A=45° ，∠B=30°，BC=8 ，求∠ACB及AC、AB的长。‎ A ‎45°‎ ‎30°‎ 四、交流体会 ‎1、什么叫做解直角三角形，它的依据是什么？‎ ‎2、解直角三角形有哪两种类型，这两种类型分别怎么解？‎ 五、达标检测 ‎1、选择题 ‎（1）下列条件下能确定各边的直角三角形是 （ ）‎ A、已知，∠C＝90° B、已知∠C＝90°，∠B＝36° ‎ C、已知，，∠C＝90° D、已知∠A＝65°，∠B＝25°‎ ‎（2）在Rt△ABC中，若∠C=90°，AC=1，BC=2，则下列结论中正确的是（ ）．‎ 3‎ A．sinB= B．cosB= C．tanB=2 D．cosB=‎ ‎（3）如图，△ABC中，∠C=90°，AB=8，cosA=，则AC的长是 ‎ ‎（4）如图，在中，是上一点，于，且，则的长为（　　　）‎ A．2 B． C． D． ‎ 如果等腰三角形的底角为30°，腰长为6cm，那么这个三角形的面积为（ ）‎ ‎ A．4.5cm2 B．9cm2 C．18cm2 D．36cm2‎ ‎2、在Rt△ABC中， 、、的对边分别是、、，∠C=90°，= ，= ，求、、∠B ‎3、在Rt△ABC中，∠C=90°解下列问题 ‎（1）已知，∠B=60°，求 ‎（2）已知，，求 ‎（3）已知 ‎4、已知等腰△ABC中，AB=AC=13，BC=10，求底角∠B的三种三角函数值． ‎ 3‎