人教版高中数学选修1-1课件：5_四种命题及其关系(3)

人教版高中数学选修1-1课件：5_四种命题及其关系(3)

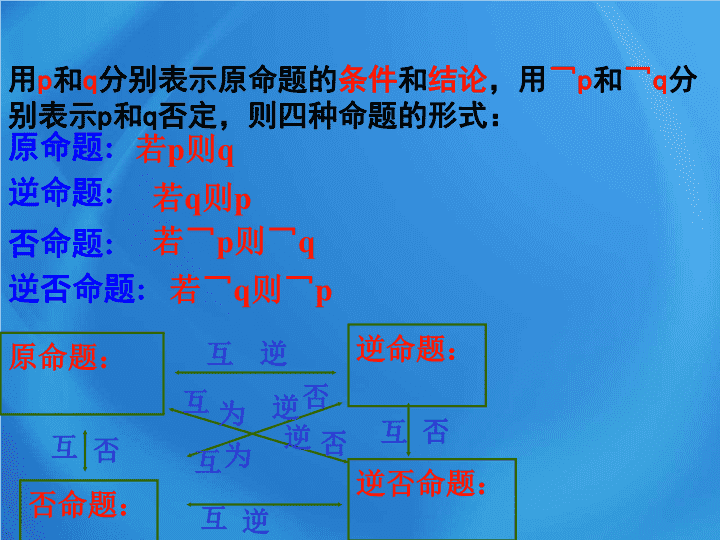
复习上节 1 、一般地，我们把用语言、符号、或式子 表达的，可以判断真假的陈述句叫 命题 。 其中判断为真的命题为 真命题 ； 其中判断为假的命题为 假命题 ； 2 、 2 2 、命题 2 、 命题可写为 “若 p 则 q” 的形式。 其中 p 称为命题的 条件 q 称为命题的 结论 3 、四种命题 2) 若两个三角形面积相等，则这两个三角形全等； 3) 若两个三角形不全等，则这两个三角形面积不相等 ; 4) 若两个三角形面积不相等，则这两个三角形不全等 l) 若两个三角形全等，则这两个三角形面积相等； 条件 结论 条件 结论 条件 结论 条件 结论 原命题 : 逆命题 : 否命题 : 逆否命题 : ( 交换原命题的条件和结论） ( 同时否定原命题的条件和结论） ( 交换原命题的条件和结论，并且同时否定 ) 原命题： 逆命题： 否命题： 逆否命题： 否 互 互 逆 互 逆 互 否 互 为 逆 否 逆 为 互 否 逆否命题 : 若￢ q 则￢ p 原命题 : 若 p 则 q 逆命题 : 若 q 则 p 用 p 和 q 分别表示原命题的 条件 和 结论 ，用 ￢ p 和 ￢ q 分别表示 p 和 q 否定，则四种命题的形式： 否命题 : 若￢ p 则￢ q (1) 若平面上两条直线平行，则这两条直线不相交。 若平面上两条直线不相交，则这两条直线平行 逆： 否 : 若平面上两条直线不平行，则这两条直线相交； 逆否 : 若平面上两条直线相交，则这两条直线不平行； (2) 若一个整数的末位数是 0 ，则这个整数能被 5 整除； 逆 : 否 : 逆否 : 若一个整数能被 5 整除，则这个整数的末位数字是 0 ； 若一个整数的末位数字不是 0 ，则这个整数不能被 5 整除； 若一个整数不能被 5 整除，则这个整数的末位数字不是 0 ； 真 真 真 真 真 假 真 假 练习：写出下列命题的其他 3 种命题，并判断真假： (3) 若 x 2 -3x+2=0 ，则 x=2 (4) 若一个数是 3 ，则这个数能被 2 整除。 逆 : 否 : 逆否 : 逆 : 否 : 逆否 : 若 x=2 ，则 x 2 -3x+2=0 ； 若 x ≠ 2 ，则 x 2 -3x+2≠0 ； 若 x 2 -3x+2≠0 ，则 x ≠ 2 ； 若一个数能被 2 整除，则这个数是 3 若一个数不是 3 ，则这个数不能被 2 整除。 若一个数不能被 2 整除，则这个数不是 3 真 真 假 假 假 假 假 假 四种命题的真假性，有且仅有下面四种情况 原命题 逆命题 否命题 逆否命题 真 假 假 假 假 真 真 真 真 真 假 假 假 假 真 真 结论： （ 1 ）两个命题互为逆否命题，它们有相同的真假性 （ 2 ）两个命题为互否命题或互逆命题，它们的真假性没有关系 小结： （ 1 ）四种命题之间的相互关系； （ 2 ）四种命题的真假性之间的关系； （ 3 ）应用： 直接证明某一个命题为真命题有困难时，可以通过证明它的逆否命题为真命题