- 2021-04-29 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教A版数系的扩充与复数的引入学案
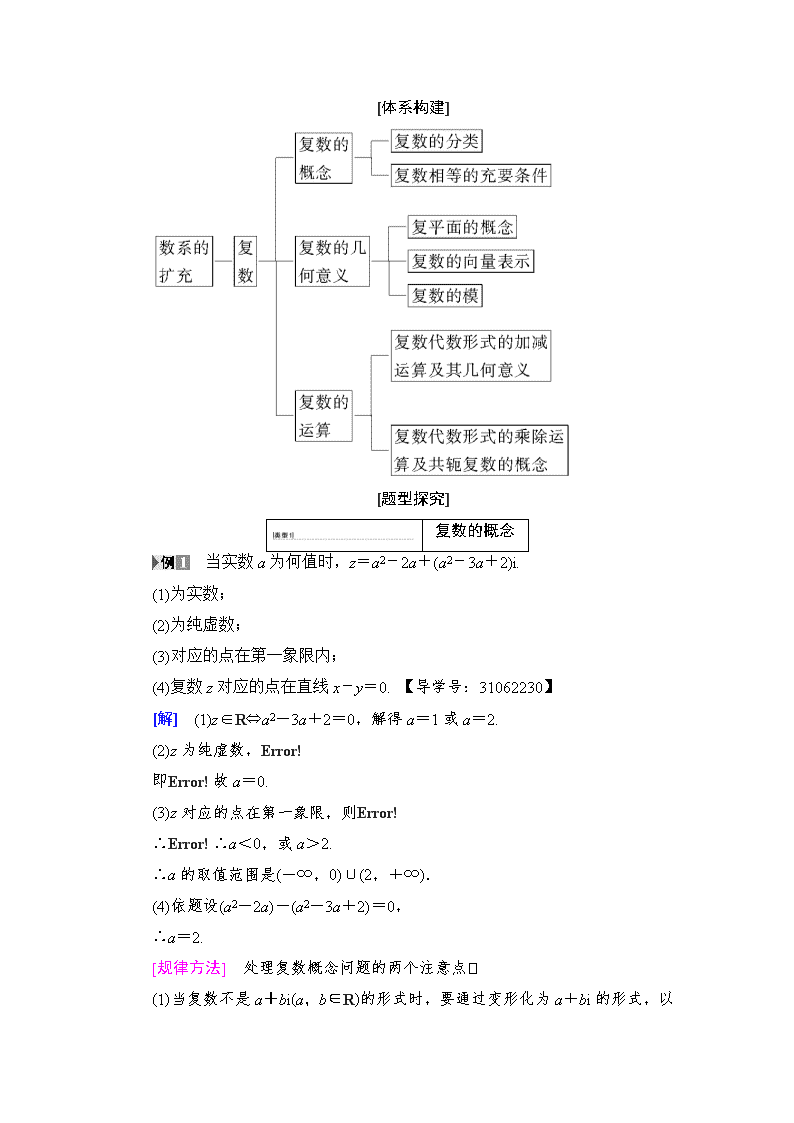
2019届一轮复习人教A版 数系的扩充与复数的引入 学案 1.复数的有关概念及分类 (1)代数形式为z=a+bi(a,b∈R),其中实部为a,虚部为b; (2)共轭复数为z=a-bi(a,b∈R). (3)复数的分类 ①若 z=a+bi(a,b∈R)是实数,则z与的关系为z=. ②若z=a+bi(a,b∈R)是纯虚数,则z与的关系为z+=0(z≠0). 2.与复数运算有关的问题 (1)复数相等的充要条件 a+bi=c+di⇔(a,b,c,d∈R). (2)复数的模 复数z=a+bi的模|z|=,且z·=|z|2=a2+b2. (3)复数的四则运算,若两个复数z1=a1+b1i,z2=a2+b2i(a1,b1,a2,b2∈R) ①加法:z1+z2=(a1+a2)+(b1+b2)i; ②减法:z1-z2=(a1-a2)+(b1-b2)i; ③乘法:z1·z2=(a1a2-b1b2)+(a1b2+a2b1)i; ④除法:==+i(z2≠0); 3.复数的几何意义 (1)任何一个复数z=a+bi一一对应着复平面内一个点Z(a,b),也一一对应着一个从原点出发的向量. (2)复数加法的几何意义 若复数z1、z2对应的向量1、2不共线,则复数z1+z2是以1、2为两邻边的平行四边形的对角线所对应的复数. (3)复数减法的几何意义 复数z1-z2是连接向量1、2的终点,并指向Z1的向量所对应的复数. [体系构建] [题型探究] 复数的概念 当实数a为何值时,z=a2-2a+(a2-3a+2)i. (1)为实数; (2)为纯虚数; (3)对应的点在第一象限内; (4)复数z对应的点在直线x-y=0. 【导学号:31062230】 [解] (1)z∈R⇔a2-3a+2=0,解得a=1或a=2. (2)z为纯虚数, 即故a=0. (3)z对应的点在第一象限,则 ∴∴a<0,或a>2. ∴a的取值范围是(-∞,0)∪(2,+∞). (4)依题设(a2-2a)-(a2-3a+2)=0, ∴a=2. [规律方法] 处理复数概念问题的两个注意点 (1)当复数不是a+bi(a,b∈R)的形式时,要通过变形化为a+b i的形式,以便确定其实部和虚部. (2)求解时,要注意实部和虚部本身对变量的要求,否则容易产生增根. [跟踪训练] 1.(1)若复数z=1+i(i为虚数单位),是z的共轭复数,则z2+2的虚部为 ( ) A.0 B.-1 C.1 D.-2 (2)设i是虚数单位,若复数a-(a∈R)是纯虚数,则a的值为( ) A.-3 B.-1 C.1 D.3 (1)A (2)D [(1)因为z=1+i,所以=1-i,所以z2+2=(1+i)2+(1-i)2=2i+(-2i)=0.故选A. (2)因为a-=a-=a-=(a-3)-i,由纯虚数的定义,知a-3=0,所以a=3.] 复数的几何意义 (1)在复平面内,复数(i是虚数单位)所对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 (2)已知复数z1=2+3i,z2=a+bi,z3=1-4i,它们在复平面上所对应的点分别为A,B,C.若=2+,则a=________,b=________. 【导学号:31062231】 (1)B (2)-3 -10 [(1)===-+i,∴复数对应的点位于第二象限. (2)∵=2+ ∴1-4i=2(2+3i)+(a+bi) 即∴] [跟踪训练] 2.若i为虚数单位,图31中复平面内点Z表示复数z,则表示复数的点是( ) 图31 A.E B.F C.G D.H D [∵点Z(3,1)对应的复数为z, ∴z=3+i,====2-i, 该复数对应的点的坐标是(2,-1),即H点.] 复数的四则运算 (1)已知是z的共轭复数,若z·i+2=2z,则z=( ) 【导学号:31062232】 A.1+i B.1-i C.-1+i D.-1-i (2)已知复数z1=2-3i,z2=,则等于( ) A.-4+3i B.3+4i C.3-4i D.4-3i (1)A (2)D [(1)设z=a+bi(a,b∈R),则=a-bi,代入z·i+2=2z中得,(a+bi)(a-bi)i+2=2(a+bi),∴2+(a2+b2)i=2a+2bi, 由复数相等的条件得, ∴ ∴z=1+i,故选A. (2)== ==4-3i.] 母题探究:1.(变结论)本例题(1)中已知条件不变,则=__________. [解析] 由解析知z=1+i,所以=1-i. ==i. [答案] i 2.(变结论)本例题(2)中已知条件不变,则z1z2=__________. [解析] z1z2= == ==-i. [答案] -i [规律方法] (1)复数的乘法运算与多项式的乘法运算类似; (2)复数的除法运算,将分子分母同时乘以分母的共轭复数,最后整理成a+bi(a,b∈R)的结构形式. (3)利用复数相等,可实现复数问题的实数化. 转化与化归思想 已知z是复数,z+2i,均为实数,且(z+ai)2的对应点在第一象限,求实数a的取值范围. 【导学号:31062233】 [解] 设z=x+yi(x,y∈R), 则z+2i=x+(y+2)i为实数,∴y=-2. 又==(x-2i)(2+i) =(2x+2)+(x-4)i为实数, ∴x=4.∴z=4-2i,又∵(z+ai)2=(4-2i+ai)2=(12+4a-a2)+8(a-2)i在第一象限. ∴,解得2查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档