【数学】2020届一轮复习人教A版变量间的相关关系与统计案例课时作业
一、选择题
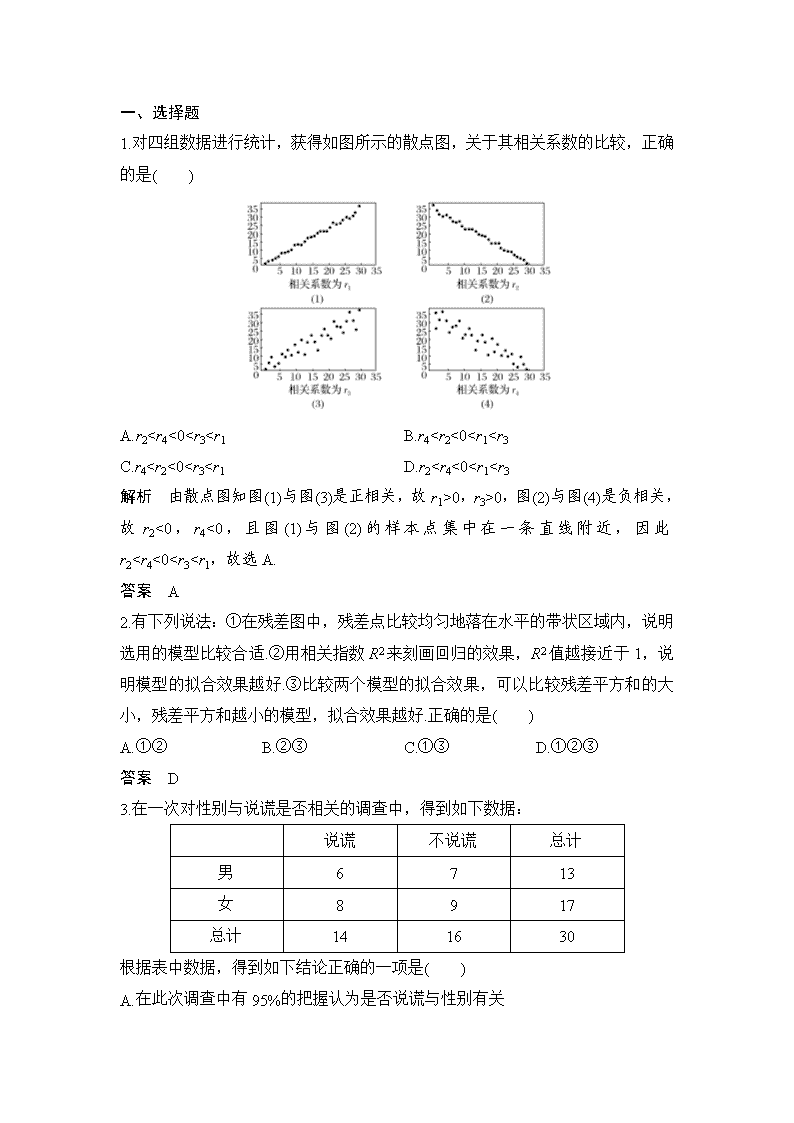
1.对四组数据进行统计,获得如图所示的散点图,关于其相关系数的比较,正确的是( )
A.r2
0,r3>0,图(2)与图(4)是负相关,故r2<0,r4<0,且图(1)与图(2)的样本点集中在一条直线附近,因此r26.635,可知我们有99%的把握认为“爱好该项运动与性别有关”.
答案 A
二、填空题
6.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温(℃)
18
13
10
-1
用电量(度)
24
34
38
64
由表中数据得回归直线方程=x+中的=-2,预测当气温为-4 ℃时,用电量约为________度.
解析 根据题意知==10,==40.所以=40-(-2)×10=60,=-2x+60.所以当x=-4时,y=(-2)×(-4)+60=68,所以用电量约为68度.
答案 68
7.(2019·济南调研)心理学家分析发现视觉和空间想象能力与性别有关,某数学兴趣小组为了验证这个结论,从所在学校中按分层抽样的方法抽取50名同学(男30,女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
根据上述数据,推断视觉和空间想象能力与性别有关系,则这种推断犯错误的概率不超过________.
附表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
解析 由列联表计算K2的观测值k=≈5.556>5.024.∴推断犯错误的概率不超过0.025.
答案 0.025
8.(2019·广东深中、华附、省实、广雅四校联考)如图是一组数据(x,y)的散点图,经最小二乘估计公式计算,y与x之间的线性回归方程为=x+1,则=________.
解析 由题图知==2,
==2.6,
将(2,2.6)代入=x+1中,解得=0.8.
答案 0.8
三、解答题
9.(2019·天津河西区调研)某厂商为了解用户对其产品是否满意,在使用该产品的用户中随机调查了80人,结果如下表:
满意
不满意
男用户
30
10
女用户
20
20
(1)根据上表,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.
P(K2≥k0)
0.100
0.050
0.025
0.010
k0
2.706
3.841
5.024
6.635
注:K2=,n=a+b+c+d.
解 (1)用分层抽样的方法在满意产品的用户中抽取5人,则抽取比例为=.
所以在满意产品的用户中应抽取女用户20×=2(人),男用户30×=3(人).
抽取的5人中,三名男用户记为a,b,c,两名女用户记为r,s,则从这5人中任选2人,共有10种情况:ab,ac,ar,as,bc,br,bs,cr,cs,rs.
其中恰好是男、女用户各1人的有6种情况:ar,as,br,bs,cr,cs.
故所求的概率为P==0.6.
(2)由题意,得K2的观测值为
k=
=≈5.333>5.024.
又P(K2≥5.024)=0.025.
故有97.5%的把握认为“产品用户是否满意与性别有关”.
10.调查某公司的五名推销员,其工作年限与年推销金额如下表:
推销员
A
B
C
D
E
工作年限x(年)
2
3
5
7
8
年推销金额y(万元)
3
3.5
4
6.5
8
(1)在图中画出年推销金额关于工作年限的散点图,并从散点图中发现工作年限与年推销金额之间关系的一般规律;
(2)利用最小二乘法求年推销金额关于工作年限的回归直线方程;
(3)利用(2)中的回归方程,预测工作年限为10年的推销员的年推销金额.
附:=,=-.
解 (1)年推销金额关于工作年限的散点图如图:
从散点图可以看出,各点散布在从左下角到右上角的区域里,因此, 工作年限与年推销金额正相关,即工作年限越长,年推销金额越大.
(2)由表中数据可得:
=×(2+3+5+7+8)=5,
=×(3+3.5+4+6.5+8)=5,
=
=
=,
=-=5-×5=,
∴年推销金额关于工作年限的回归直线方程为
=x+.
(3)当x=10时,=×10+=,
∴预测工作年限为10年的推销员的年推销金额为万元.
能力提升题组
(建议用时:20分钟)
11.在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A.若K2的观测值为k=6.635,在犯错误的概率不超过0.01的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌
B.由独立性检验可知,在犯错误的概率不超过0.01的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有99%的可能患有肺癌
C.若从统计量中求出在犯错误的概率不超过0.01的前提下认为吸烟与患肺癌有关系,是指有1%的可能性使得判断出现错误
D.以上三种说法都不正确
解析 独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论,因此才出现了临界值表,在分析问题时一定要注意这点,不可对某个问题下确定性结论,否则就可能对统计计算的结果作出错误的解释.若从统计量中求出在犯错误的概率不超过0.01的前提下认为吸烟与患肺癌有关系,是指有1%的可能性使得判断出现错误.故选C.
答案 C
12.(2019·承德期末)某城市收集并整理了该市2018年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.
已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论错误的是( )
A.最低气温与最高气温为正相关
B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月
D.最低气温低于0 ℃的月份有4个
解析 在A中,最低气温与最高气温为正相关,故A正确;在B中,10月的最高气温不低于5月的最高气温,故B正确;在
C中,月温差(最高气温减最低气温)的最大值出现在1月,故C正确;在D中,最低气温低于0 ℃的月份有3个,故D错误.故选D.
答案 D
13.在2018年3月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
价格x
9
9.5
m
10.5
11
销售量y
11
n
8
6
5
由散点图可知,销售量y与价格x之间有较强的线性相关关系,其线性回归方程是=-3.2x+40,且m+n=20,则其中的n=________.
解析 ==8+,
==6+.
回归直线一定经过样本中心(,),
即6+=-3.2+40,即3.2m+n=42.
又因为m+n=20,即
解得故n=10.
答案 10
14.(2019·山东、湖北部分重点中学模拟)某地级市共有200 000名中小学生,其中有7%的学生在2017年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为5∶3∶2,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助1 000元、1 500元、2 000元.经济学家调查发现,当地人均可支配收入较上一年每增加有n%,一般困难的学生中有3n%会脱贫,脱贫后将不再享受“国家精准扶贫”政策,很困难的学生中有2n%转为一般困难,特别困难的学生中有n%转为很困难.
现统计了该地级市2013年到2017年共5年的人均可支配收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份x取13时代表2013年,x与y(万元)近似满足关系式y=C1·2C2x,其中C1,C2为常数.(2013年至2019年该市中学生人数大致保持不变)
(ki-)2
(yi-)2
(xi-)(yi-)
(xi-)(ki-)
2.3
1.2
3.1
4.6
2
1
其中ki=log2 yi,=ki.
(1)估计该市2018年人均可支配收入;
(2)求该市2018年的“专项教育基金”的财政预算大约为多少.
附:①对于一组具有线性相关关系的数据(u1,v1),(u2,v2),…,(un,vn),其回归直线方程=u+的斜率和截距的最小二乘估计分别为=,=-.
②
2-0.7
2-0.3
20.1
21.7
21.8
21.9
0.6
0.8
1.1
3.2
3.5
3.73
解 (1)因为=×(13+14+15+16+17)=15,所以 (xi-)2=(-2)2+(-1)2+02+12+22=10.
由k=log2 y得k=log2 C1+C2x,
所以C2==,
log2 C1=-C2=1.2-×15=-0.3,
所以C1=2-0.3=0.8,
所以y=0.8×2.
当x=18时,y=0.8×21.8=0.8×3.5=2.8(万元).
即该市2018年人均可支配收入为2.8万元.
(2)由题意知2017年时该市享受“国家精准扶贫”政策的学生有200 000×7%=14 000人,
一般困难、很困难、特别困难的中学生依次有7 000人、4 200人、2 800人,2018年人均可支配收入比2017年增长=20.1-1=0.1=10%,
所以2018年该市特别困难的中学生有2 800×(1-10%)=2 520人.
很困难的的学生有4 200×(1-20%)+2 800×10%=3 640人,
一般困难的学生有7 000×(1-30%)+4 200×20%=5 740人.
所以2018年的“专项教育基金”的财政预算大约为5 740×1 000+3 640×1 500+2 520×2 000=16 240 000(元)=1 624(万元).