【数学】2018届一轮复习人教A版 空间向量及其运算 学案

【数学】2018届一轮复习人教A版 空间向量及其运算 学案

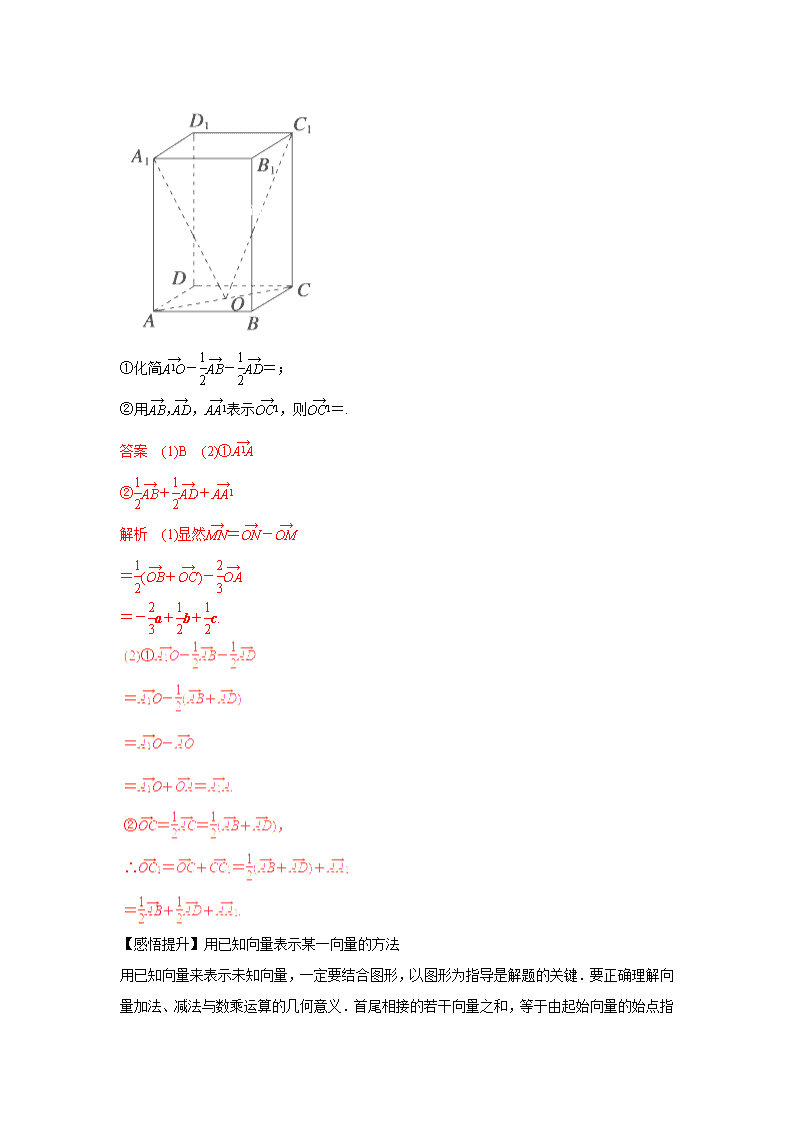
专题43 空间向量及其运算 ‎1.了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示；2.掌握空间向量的线性运算及其坐标表示；‎ ‎3.掌握空间向量的数量积及其坐标表示，能用向量的数量积判断向量的共线和垂直.‎ ‎ ‎ ‎1．空间向量的有关概念 名称 概念 表示 零向量 模为0的向量 ‎0‎ 单位向量 长度(模)为1的向量 相等向量 方向相同且模相等的向量 a＝b 相反向量 方向相反且模相等的向量 a的相反向量为－a 共线向量 表示空间向量的有向线段所在的直线互相平行或重合 a∥b 共面向量 平行于同一个平面的向量 ‎2.共线向量、共面向量定理和空间向量基本定理 ‎(1)共线向量定理：对空间任意两个向量a，b(b≠0)，a∥b的充要条件是存在实数λ，使得a＝λb．‎ ‎(2)共面向量定理：若两个向量a，b不共线，则向量p与向量a，b共面⇔存在唯一的有序实数对(x，y)，使p＝xa＋yb．‎ ‎(3)空间向量基本定理：如果三个向量a，b，c不共面，那么对空间任一向量p，存在有序实数组{x，y，z}，使得p＝xa＋yb＋zc，把{a，b，c}叫做空间的一个基底．‎ ‎3．空间向量的数量积及运算律 ‎(1)数量积及相关概念 ‎①两向量的夹角 已知两个非零向量a，b，在空间任取一点O，作＝a，＝b，则∠AOB叫做向量a与b的夹角，记作〈a，b〉，其范围是0≤〈a，b〉≤π，若〈a，b〉＝，则称a与b互相垂直，记作a⊥b.‎ ‎②两向量的数量积 已知空间两个非零向量a，b，则|a||b|cos〈a，b〉叫做向量a，b的数量积，记作a·b，即a·b＝|a||b|cos〈a，b〉．‎ ‎(2)空间向量数量积的运算律 ‎①结合律：(λa)·b＝λ(a·b)；‎ ‎②交换律：a·b＝b·a；‎ ‎③分配律：a·(b＋c)＝a·b＋a·c．‎ ‎4．空间向量的坐标表示及其应用 设a＝(a1，a2，a3)，b＝(b1，b2，b3).‎ 向量表示 坐标表示 数量积 a·b a1b1＋a2b2＋a3b3‎ 共线 a＝λb(b≠0)‎ a1＝λb1，a2＝λb2，a3＝λb3‎ 垂直 a·b＝0‎ ‎(a≠0，b≠0)‎ a1b1＋a2b2＋a3b3＝0‎ 模 ‎|a|‎ 夹角 ‎〈a，b〉(a≠0，b≠0)‎ cos〈a，b〉＝ 高频考点一　空间向量的线性运算 例1、(1)已知在空间四边形OABC中，＝a，＝b，＝c，点M在OA上，且OM＝2MA，N为BC中点，则等于(　　)‎ A.a－b＋c B．－a＋b＋c C.a＋b－c D.a＋b－c ‎(2)如图所示，在长方体ABCD－A1B1C1D1中，O为AC的中点．‎ ‎①化简－－＝；‎ ‎②用，，表示，则＝.‎ 答案　(1)B　(2)① ‎②＋＋ 解析　(1)显然＝－ ‎＝(＋)－ ‎＝－a＋b＋c.‎ ‎【感悟提升】用已知向量表示某一向量的方法 用已知向量来表示未知向量，一定要结合图形，以图形为指导是解题的关键．要正确理解向量加法、减法与数乘运算的几何意义．首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量．在立体几何中三角形法则、平行四边形法则仍然成立． ‎ ‎【变式探究】三棱锥O－ABC中，M，N分别是OA，BC的中点，G是△ABC的重心，用基向量，，表示，.‎ 解　＝＋＝＋ ‎＝＋(－)‎ ‎＝＋[(＋)－]‎ ‎＝－＋＋.‎ ＝＋＝－＋＋ ‎＝＋＋.‎ 高频考点二　共线定理、共面定理的应用 例2、已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点，‎ ‎(1)求证：E、F、G、H四点共面；‎ ‎(2)求证：BD∥平面EFGH；‎ ‎(3)设M是EG和FH的交点，求证：对空间任一点O，有＝(＋＋＋)．‎ 证明　(1)如图，连接BG，‎ 则＝＋ ‎＝＋(＋)‎ ‎＝＋＋＝＋，‎ 由共面向量定理的推论知：‎ E、F、G、H四点共面．‎ ‎(2)因为＝－ ‎＝－＝(－)＝，‎ 所以EH∥BD.‎ 又EH⊂平面EFGH，BD⊄平面EFGH，‎ 所以BD∥平面EFGH.‎ ‎(3)找一点O，并连接OM，OA，OB，OC，OD，OE，OG，如图所示．‎ 由(2)知＝，同理＝，‎ 所以＝，即EH綊FG，‎ 所以四边形EFGH是平行四边形．‎ 所以EG，FH交于一点M且被M平分．‎ 故＝(＋)＝＋ ‎＝＋ ‎＝(＋＋＋)．‎ ‎【感悟提升】(1)证明点共线的方法 证明点共线的问题可转化为证明向量共线的问题，如证明A，B，C三点共线，即证明，共线，亦即证明＝λ(λ≠0)．‎ ‎(2)证明点共面的方法 证明点共面问题可转化为证明向量共面问题，如要证明P，A，B，C四点共面，只要能证明＝x＋y或对空间任一点O，有＝＋x＋y或＝x＋y＋z(x＋y＋z＝1)即可．共面向量定理实际上也是三个非零向量所在直线共面的充要条件．‎ ‎【变式探究】如图，正方体ABCD－A1B1C1D1中，E是A1B上的点，F是AC上的点，且A1E＝2EB，CF＝2AF，则EF与平面A1B1CD的位置关系为．‎ 高频考点三　空间向量数量积的应用 例3、如图所示，已知空间四边形ABCD的各边和对角线的长都等于a，点M、N分别是AB、CD的中点．‎ ‎(1)求证：MN⊥AB，MN⊥CD；‎ ‎(2)求MN的长；‎ ‎(3)求异面直线AN与CM所成角的余弦值．‎ ‎(1)证明　设＝p，＝q，＝r.‎ 由题意可知，|p|＝|q|＝|r|＝a，且p、q、r三向量两两夹角均为60°.‎ ＝－＝(＋)－ ‎＝(q＋r－p)，‎ ‎∴·＝(q＋r－p)·p ‎＝(q·p＋r·p－p2)‎ ‎＝(a2cos60°＋a2cos60°－a2)＝0.‎ ‎∴⊥.即MN⊥AB.‎ 同理可证MN⊥CD.‎ ‎(2)解　由(1)可知＝(q＋r－p)，‎ ‎∴||2＝(q＋r－p)2‎ ‎＝[q2＋r2＋p2＋2(q·r－p·q－r·p)]‎ ‎＝[a2＋a2＋a2＋2(－－)]＝×2a2＝.‎ ‎∴||＝a.∴MN的长为a.‎ ‎(3)解　设向量与的夹角为θ.‎ ‎∵＝(＋)＝(q＋r)，‎ ＝－＝q－p，‎ ‎∴·＝(q＋r)·(q－p)‎ ‎＝(q2－q·p＋r·q－r·p)‎ ‎＝(a2－a2cos60°＋a2cos60°－a2cos60°)‎ ‎＝(a2－＋－)＝.‎ 又∵||＝||＝a，‎ ‎∴·＝||||cosθ＝a×a×cosθ＝.‎ ‎∴cosθ＝.‎ ‎∴向量与的夹角的余弦值为，从而异面直线AN与CM所成角的余弦值为.‎ ‎【方法技巧】数量积的应用 ‎(1)求夹角，设向量a，b所成的角为θ，则cosθ＝，进而可求两异面直线所成的角；‎ ‎(2)求长度(距离)，运用公式|a|2＝a·a，可使线段长度的计算问题转化为向量数量积的计算问题；‎ ‎(3)解决垂直问题，利用a⊥b⇔a·b＝0(a≠0，b≠0)，可将垂直问题转化为向量数量积的计算问题。‎ ‎【变式探究】如图所示，四棱柱ABCD－A1B1C1D1中，底面为平行四边形，以顶点A为端点的三条棱长都为1，且两两夹角为60°.‎ ‎(1)求AC1的长；‎ ‎(2)求证：AC1⊥BD；‎ ‎(3)求BD1与AC夹角的余弦值．‎ 解　(1)记＝a，＝b，＝c，‎ 则|a|＝|b|＝|c|＝1，〈a，b〉＝〈b，c〉＝〈c，a〉＝60°，‎ ‎∴a·b＝b·c＝c·a＝.‎ ‎||2＝(a＋b＋c)2＝a2＋b2＋c2＋2(a·b＋b·c＋c·a)‎ ‎＝1＋1＋1＋2×(＋＋)＝6，‎ ‎∴||＝，即AC1的长为.‎ ‎(2)∵＝a＋b＋c，‎ ＝b－a，‎ ‎∴·＝(a＋b＋c)(b－a)‎ ‎＝a·b＋|b|2＋b·c－|a|2－a·b－a·c ‎＝b·c－a·c ‎＝|b|·|c|cos60°－|a||c|cos60°＝0.‎ ‎∴⊥，∴AC1⊥BD.‎ ‎1.【2016高考新课标2理数】如图，菱形的对角线与交于点，，点分别在上，，交于点．将沿折到位置，．‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）求二面角的正弦值．‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ ‎【解析】‎ ‎（Ⅰ）由已知得，，又由得，故.‎ 因此，从而.由,得.‎ 由得.所以，.‎ 于是，‎ 故. ‎ 又，而，‎ 所以.‎ ‎（Ⅱ）如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系，则，，，，，，，.设是平面的法向量，则，即，所以可取.设是平面的法向量，则，即，所以可取.于是， .因此二面角的正弦值是.‎ ‎2.【2016高考山东理数】在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O的直径，FB是圆台的一条母线.‎ ‎（I）已知G,H分别为EC，FB的中点，求证：GH∥平面ABC；‎ ‎（II）已知EF=FB=AC=，AB=BC.求二面角的余弦值.‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）‎ ‎【解析】‎ ‎（II）解法一：‎ 连接,则平面，‎ 又且是圆的直径，所以 以为坐标原点，建立如图所示的空间直角坐标系，‎ 由题意得，，过点作于点，‎ 所以 可得 故.‎ 设是平面的一个法向量. ‎ 由 可得 可得平面的一个法向量 因为平面的一个法向量 所以.‎ 所以二面角的余弦值为.‎ 从而为二面角的平面角.‎ 又,是圆的直径，‎ 所以 从而，可得 所以二面角的余弦值为.‎ ‎3.【2016高考天津理数】（本小题满分13分）‎ 如图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.‎ ‎（I）求证：EG∥平面ADF；‎ ‎（II）求二面角O-EF-C的正弦值；‎ ‎（III）设H为线段AF上的点，且AH=HF，求直线BH和平面CEF所成角的正弦值.‎ ‎【答案】（Ⅰ）详见解析（Ⅱ）（Ⅲ）‎ ‎【解析】依题意，，如图，以为点，分别以的方向为轴，轴、轴的正方向建立空间直角坐标系，依题意可得，.‎ ‎（I）证明：依题意，.设为平面的法向量，则，即 .不妨设，可得，又，可得，又因为直线，所以.‎ ‎（III）解：由，得.因为，所以，进而有，从而，因此.所以，直线和平面所成角的正弦值为.‎ ‎4.【2016年高考北京理数】（本小题14分）‎ 如图，在四棱锥中，平面平面，，，，‎ ‎，，.‎ ‎（1）求证：平面；‎ ‎（2）求直线与平面所成角的正弦值；‎ ‎（3）在棱上是否存在点，使得平面？若存在，求的值；若不存在，说明理由.‎ ‎【答案】（1）见解析；（2）；（3）存在，‎ ‎【解析】（1）因为平面平面，，‎ 所以平面，所以，‎ 又因为，所以平面；‎ ‎（2）取的中点，连结，，‎ 因为，所以.‎ 又因为平面，平面平面，‎ 所以平面.‎ 因为平面，所以.‎ 因为，所以.‎ 如图建立空间直角坐标系，由题意得，‎ ‎.‎ 设平面的法向量为，则 即 令，则.‎ 所以.‎ 又，所以.‎ 所以直线与平面所成角的正弦值为.‎ ‎（3）设是棱上一点，则存在使得.‎ 因此点.‎ 因为平面，所以平面当且仅当，‎ 即，解得.‎ 所以在棱上存在点使得平面，此时.‎ ‎5.【2016高考浙江理数】(本题满分15分)如图,在三棱台中,平面平面 ‎,,BE=EF=FC=1,BC=2,AC=3.‎ ‎(I)求证：EF⊥平面ACFD；‎ ‎(II)求二面角B-AD-F的平面角的余弦值.‎ ‎【答案】（I）证明见解析；（II）．‎ ‎【解析】（Ⅰ）延长，，相交于一点，如图所示．‎ 因为平面平面，且，所以平面，因此．‎ 又因为，，，‎ 所以为等边三角形，且为的中点，则．‎ 所以平面．‎ ‎（Ⅱ）方法一：过点作于Q，连结．‎ 因为平面，所以，则平面，所以．‎ 所以是二面角的平面角．‎ 在中，，，得．‎ 在中，，，得．‎ 所以二面角的平面角的余弦值为．‎ 方法二：如图，延长，，相交于一点，则为等边三角形．‎ 取的中点，则，又平面平面，所以，平面．‎ 以点为原点，分别以射线，的方向为，的正方向，建立空间直角坐标系．‎ 由题意得，，，，，．‎ 因此，，，．‎ 设平面的法向量为，平面的法向量为．‎ 由，得，取；‎ 由，得，取．‎ 于是，．‎ 所以，二面角的平面角的余弦值为．‎ ‎6.【2016年高考四川理数】（本小题满分12分）‎ 如图，在四棱锥P-ABCD中，AD∥BC，ADC=PAB=90°，BC=CD=AD，E为边AD的中点，异面直线PA与CD所成的角为90°. ‎ ‎（Ⅰ）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；‎ ‎（Ⅱ）若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值.‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ ‎【解析】（Ⅰ）在梯形ABCD中，AB与CD不平行.‎ 延长AB，DC，相交于点M（M∈平面PAB），点M即为所求的一个点.理由如下：‎ 由已知，BC∥ED，且BC=ED.‎ 所以四边形BCDE是平行四边形.，所以CD∥EB 从而CM∥EB.‎ 又EB平面PBE，CM平面PBE，‎ 所以CM∥平面PBE.‎ ‎（说明：延长AP至点N，使得AP=PN，则所找的点可以是直线MN上任意一点）‎ ‎（Ⅱ）方法一：‎ 由已知，CD⊥PA，CD⊥AD，PAAD=A，‎ 所以CD⊥平面PAD.‎ 从而CD⊥PD.‎ 所以∠PDA是二面角P-CD-A的平面角.‎ 所以∠PDA=45°.‎ 设BC=1，则在Rt△PAD中，PA=AD=2.‎ 过点A作AH⊥CE，交CE的延长线于点H，连接PH.‎ 易知PA⊥平面ABCD，‎ 从而PA⊥CE.‎ 于是CE⊥平面PAH.‎ 所以平面PCE⊥平面PAH.‎ 过A作AQ⊥PH于Q，则AQ⊥平面PCE.‎ 所以∠APH是PA与平面PCE所成的角.‎ 在Rt△AEH中，∠AEH=45°，AE=1，‎ 所以AH=.‎ 在Rt△PAH中，PH== ，‎ 所以sin∠APH= =.‎ 方法二：‎ 作Ay⊥AD，以A为原点，以 ,的方向分别为x轴，z轴的正方向，建立如图所示的空间直角坐标系A-xyz，则A（0,0,0），P（0,0,2），C(2,1,0)，E(1,0,0)，‎ 所以=（1,0,-2），=（1,1,0），=（0,0,2）‎ 设平面PCE的法向量为n=(x,y,z)，‎ 由 得 设x=2，解得n=(2,-2,1).‎ 设直线PA与平面PCE所成角为α，则sinα= = .‎ 所以直线PA与平面PCE所成角的正弦值为 .‎ ‎【2015高考湖南，理19】如图，已知四棱台上、下底面分别是边长为3和6的正方形，，且底面，点，分别在棱，BC上.‎ ‎（1）若P是的中点，证明：；‎ ‎（2）若平面，二面角的余弦值为，求四面体的体积.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ 解法一 由题设知，，，两两垂直，以为坐标原点，，，所在直线分别为轴，轴，轴，建立如图b所示的空间直角坐标系，则相关各点的坐标为，，‎ ‎， ， ，其中，，‎ ‎（1）若是的中点，则，，于是，∴，即；（2）由题设知，，是平面内的两个不共线向量.‎ 设是平面的一个法向量，则，即，‎ 取，得，又平面的一个法向量是，‎ ‎∴，而二面角的余弦值为，因此，解得，或者（舍去），此时，‎ 设，而，由此得点，‎ ‎，∵平面，且平面的一个法向量是，‎ ‎∴，即，亦即，从而，于是，将四面体视为以为底面的三棱锥，则其高，故四面体的体积.‎ ‎（2）如图d，过点作交于点，则平面，‎ ‎∵平面，∴平面，过点作于点，连结，则，为二面角的平面角，∴，即，从而③‎ 连结，由平面，∴，又是正方形，所以为矩形，故，设，则 ④，过点作交于点，则为矩形，∴，，因此，于是，∴，再由③④得，解得，因此，故四面体的体积.‎ ‎【2015高考上海，理19】（本题满分12分）如图，在长方体中，，，、分别是、的中点．证明、、、四点共面，并求直线与平面所成的角的大小.‎ ‎【答案】‎ ‎ 【解析】解：如图，以为原点建立空间直角坐标系，可得有关点的坐标为、、、、、．‎ 因为，，‎ 所以，因此直线与共面，‎ 即、、、共面．‎ 设平面的法向量为，则，，‎ 又，，‎ 故，解得．‎ 取，得平面的一个法向量．又，‎ 故．‎ 因此直线与平面所成的角的大小为．‎ ‎1．（2014·广东卷）已知向量a＝(1，0，－1)，则下列向量中与a成60°夹角的是(　　)‎ A．(－1，1，0) B．(1，－1，0) ‎ C．(0，－1，1) D．(－1，0，1)‎ ‎【答案】B　【解析】本题考查空间直角坐标系中数量积的坐标表示．设所求向量是b，若b与a成60°夹角，则根据数量积公式，只要满足＝即可，所以B选项满足题意．‎ ‎2．（2014·重庆卷]如图13所示，四棱锥PABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB＝2，∠BAD＝，M为BC上一点，且BM＝，MP⊥AP.‎ ‎(1)求PO的长；‎ ‎(2)求二面角APMC的正弦值．‎ 图13‎ ‎【解析】解：(1)如图所示，连接AC，BD，因为四边形ABCD为菱形，所以AC∩ BD＝O，且AC⊥BD.以O为坐标原点，，，的方向分别为x轴，y轴，z轴的正方向建立空间直角坐标系O xyz.‎ 因为∠BAD＝，‎ 所以OA＝AB·cos＝，OB＝AB·sin＝1，‎ 所以O(0，0，0)，A(，0，0)，B(0，1，0)，C(－，0，0)，＝(0，1，0)，＝(－，－1，0)．‎ 由BM＝，BC＝2知，＝＝，‎ 从而＝＋＝，‎ 即M.‎ 设P(0，0，a)，a＞0，则＝(－，0，a)，＝.因为MP⊥AP，所以·＝0，即－＋a2＝0，所以a＝或a＝－(舍去)，即PO＝.‎ 由n2·＝0，n2·＝0，得 故可取n2＝(1，－，－2)．‎ 从而法向量n1，n2的夹角的余弦值为 cos〈n1，n2〉＝＝－，‎ 故所求二面角APMC的正弦值为.‎ ‎1．在下列命题中：‎ ‎①若向量a，b共线，则向量a，b所在的直线平行；‎ ‎②若向量a，b所在的直线为异面直线，则向量a，b一定不共面；‎ ‎③若三个向量a，b，c两两共面，则向量a，b，c共面；‎ ‎④已知空间的三个向量a，b，c，则对于空间的任意一个向量p总存在实数x，y，z使得p＝xa＋yb＋zc.‎ 其中正确命题的个数是(　　)．‎ A．0 B．1‎ C．2 D．3‎ 答案　A ‎2．已知a＝(－2,1,3)，b＝(－1,2,1)，若a⊥(a－λb)，则实数λ的值为(　　)‎ A．－2 B．－ C. D．2‎ 答案　D 解析　由题意知a·(a－λb)＝0，即a2－λa·b＝0，‎ 所以14－7λ＝0，解得λ＝2.‎ ‎3．已知{a，b，c}是空间的一个基底，{a＋b，a－b，c}是空间的另一个基底，一向量p在基底{a，b，c}下的坐标为(4,2,3)，则向量p在基底{a＋b，a－b，c}下的坐标是(　　)‎ A．(4,0,3) B．(3,1,3)‎ C．(1,2,3) D．(2,1,3)‎ 答案　B 解析　设p在基底{a＋b，a－b，c}下的坐标为x，y，z.‎ 则p＝x(a＋b)＋y(a－b)＋zc ‎＝(x＋y)a＋(x－y)b＋zc，①‎ 因为p在{a，b，c}下的坐标为(4,2,3)‎ ‎∴p＝4a＋2b＋3c，②‎ 由①②得∴ 即p在{a＋b，a－b，c}下的坐标为(3,1,3)．‎ ‎4．空间四边形ABCD的各边和对角线均相等，E是BC的中点，那么(　　)‎ A.·<· B.·＝· C.·>· D.·与·的大小不能比较 答案　C 解析　取BD的中点F，连接EF，则EF綊CD，因为〈，〉＝〈，〉>90°，因为·＝0，·<0，所以·>·.‎ ‎5．已知a，b是异面直线，A，B∈a，C，D∈b，AC⊥b，BD⊥b且AB＝2，CD＝1，则异面直线a，b所成的角等于(　　)‎ A．30°B．45°‎ C．60°D．90°‎ 答案　C 解析　如图，设＝a，＝b，＝c，则＝a＋b＋c，‎ 所以cos〈，〉＝＝，‎ 所以异面直线a，b所成的角等于60°，‎ 故选C.‎ ‎6．在空间四边形ABCD中，则·＋·＋·的值为．‎ 答案　0‎ 解析　方法一　‎ 如图，令＝a，＝b，＝c，‎ 则·＋·＋· ‎＝·(－)＋·(－)＋·(－)‎ ‎＝a·(c－b)＋b·(a－c)＋c·(b－a)‎ ‎＝a·c－a·b＋b·a－b·c＋c·b－c·a ‎＝0.‎ 方法二　‎ 如图，在三棱锥A－BCD中，不妨令其各棱长都相等，则正四面体的对棱互相垂直．‎ ‎∴·＝0，·＝0，‎ ·＝0.‎ ‎∴·＋·＋·＝0.‎ ‎7．A，B，C，D是空间不共面四点，且·＝0，·＝0，·＝0，则△BCD的形状是三角形(填锐角、直角、钝角中的一个)．‎ 答案　锐角 解析　因为·＝(－)·(－)‎ ‎＝·－·－·＋2‎ ‎＝2>0，‎ 所以∠CBD为锐角．‎ 同理∠BCD，∠BDC均为锐角．‎ ‎8．设O－ABC是四面体，G1是△ABC的重心，G是OG1上的一点，且OG＝3GG1，若＝x＋y＋z，则(x，y，z)为．‎ 答案　(，，)‎ 解析　‎ 如图所示，取BC的中点E，连接AE.‎ ＝ ‎＝(＋)‎ ‎＝＋ ‎＝＋(＋)‎ ‎＝＋(－＋－)‎ ‎＝(＋＋)，‎ ‎∴x＝y＝z＝.‎ ‎9．已知空间中三点A(－2,0,2)，B(－1,1,2)，C(－3,0,4)，设a＝，b＝.‎ ‎(1)求向量a与向量b的夹角的余弦值；‎ ‎(2)若ka＋b与ka－2b互相垂直，求实数k的值．‎ 解　(1)∵a＝(1,1,0)，b＝(－1,0,2)，‎ ‎∴a·b＝(1,1,0)·(－1,0,2)＝－1，‎ 又|a|＝＝，‎ ‎|b|＝＝，‎ ‎∴cos〈a，b〉＝＝＝－，‎ 即向量a与向量b的夹角的余弦值为－.‎ ‎(2)方法一　∵ka＋b＝(k－1，k,2)．‎ ka－2b＝(k＋2，k，－4)，‎ 且ka＋b与ka－2b互相垂直，‎ ‎∴(k－1，k,2)·(k＋2，k，－4)‎ ‎＝(k－1)(k＋2)＋k2－8＝0，‎ ‎∴k＝2或k＝－，‎ ‎∴当ka＋b与ka－2b互相垂直时，‎ 实数k的值为2或－.‎ 方法二　由(1)知|a|＝，|b|＝，a·b＝－1，‎ ‎∴(ka＋b)·(ka－2b)＝k2a2－ka·b－2b2‎ ‎＝2k2＋k－10＝0，得k＝2或k＝－.‎ ‎∴当ka＋b与ka－2b互相垂直时，实数k的值为2或－.‎ ‎10.如图，在棱长为a的正方体OABC－O1A1B1C1中，E、F分别是棱AB、BC上的动点，且AE＝BF＝x，其中0≤x≤a，以O为原点建立空间直角坐标系Oxyz.‎ ‎(1)写出点E、F的坐标；‎ ‎(2)求证：A1F⊥C1E；‎ ‎(3)若A1、E、F、C1四点共面，求证：＝＋.‎ ‎(1)解　E(a，x,0)，F(a－x，a,0)．‎ ‎ ‎ ‎(3)证明　∵A1、E、F、C1四点共面，‎ ‎∴、、共面．‎ 选与为在平面A1C1E上的一组基向量，则存在唯一实数对(λ1，λ2)，使＝λ1＋λ2，‎ 即(－x，a，－a)＝λ1(－a，a,0)＋λ2(0，x，－a)‎ ‎＝(－aλ1，aλ1＋xλ2，－aλ2)，‎ ‎∴ 解得λ1＝，λ2＝1.‎ 于是＝＋.‎