新人教版八年级数学上册全册单元检测题（共5单元附答案）

新人教版八年级数学上册全册单元检测题（共5单元附答案）

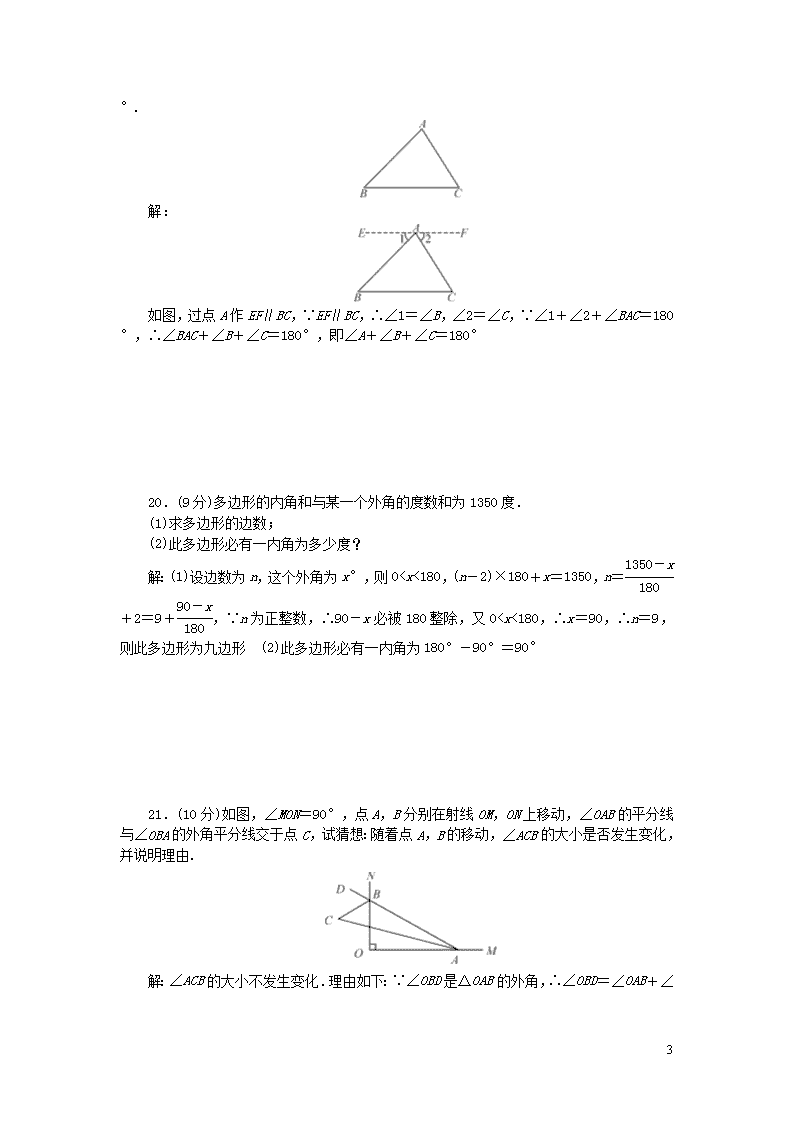
1 第十一章检测题 (时间：100 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．(百色中考)在△OAB 中，∠O＝90°，∠A＝35°，则∠B＝( B ) A．35° B．55° C．65° D．145° 2．(柳州中考)如图，图中直角三角形共有( C ) A．1 个 B．2 个 C．3个 D．4 个 第 2 题图 第 4 题图 第 5 题图 3．(2019·毕节)在下列长度的三条线段中，不能组成三角形的是( C ) A．2 cm，3 cm，4 cm B．3 cm，6 cm，6 cm C．2 cm，2 cm，6 cm D．5 cm，6 cm，7 cm 4．如图，CD 平分含 30°角的三角板的∠ACB，则∠1等于( B ) A．110° B．105° C．100° D．95° 5．(2019·广西)将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为( C ) A．60° B．65° C．75° D．85° 6．(2019·鞍山)如图，某人从点 A 出发，前进 8 m 后向右转 60°，再前进 8 m 后又向 右转 60°，按照这样的方式一直走下去，当他第一次回到出发点 A时，共走了( D ) A．24 m B．32 m C．40 m D．48 m 7．如图，AD 是△ABC 的中线，CE 是△ACD 的中线，DF 是△CDE 的中线，若 S△DEF＝2，则 S△ABC等于( A ) A．16 B．14 C．12 D．10 第 6 题图 第 7 题图 第 8 题图 第 9 题图 8．如图，在四边形 ABCD 中，点 M，N分别在 AB，BC 上，将△BMN 沿 MN 翻折得到△FMN， 若 MF∥AD，FN∥DC，则∠D 的度数为( C ) A．115° B．105° C．95° D．85° 9．(济宁中考)如图，在五边形 ABCDE 中，∠A＋∠B＋∠E＝300°，DP，CP 分别平分∠ EDC，∠BCD，则∠P＝( C ) 2 A．50° B．55° C．60° D．65° 10．(2019·扬州)已知 n 是正整数，若一个三角形的三边长分别是 n＋2，n＋8，3n， 则满足条件的 n的值有( D ) A．4 个 B．5 个 C．6个 D．7 个 二、填空题(每小题 3 分，共 15 分) 11．(2019·济南)一个 n边形的内角和等于 720°，则 n＝__6__． 12．在△ABC 中，∠A＋∠B＝2∠C，则∠C＝60°． 13．如图，在△ABC 中，BD 是 AC 边上的高，CE 是 AB 边上的高，BD 与 CE 相交于点 O， 则∠ABD__＝__∠ACE(填“＞”“＜”或“＝”)，∠A＋∠DOE＝180 度． 第 13 题图 第 14 题图 第 15 题图 14．(邵阳中考)如图所示，在四边形 ABCD 中，AD⊥AB，∠C＝110°，它的一个外角∠ ADE＝60°，则∠B 的大小是 40°． 15．如图，图①中的多边形(边数为 12)由正三角形“扩展”而来的，图②中的多边形(边 数为 20)是由正方形“扩展”而来的……依次类推，则由正 n 边形“扩展”而来的多边形的 边数为 n(n＋1)． 三、解答题(共 75 分) 16．(8 分)如图，在△ABC 中，∠A＝90°，∠ACB 的平分线交 AB 于点 D，已知∠DCB＝2 ∠B，求∠ACD 的度数． 解：设∠B＝x°，可得∠DCB＝2x°，∵CD 平分∠BCA，∴∠ACD＝∠BCD＝2x°，则 x ＋2x＋2x＝90，∴x＝18，∴∠ACD＝2x°＝36° 17．(9 分)如图，在△ABC 中，AD 是高，AE 是角平分线，∠B＝70°，∠DAE＝18°，求 ∠C 的度数． 3 解：由题意知∠BAD＝90°－∠B＝20°，∴∠BAE＝∠BAD＋∠DAE＝38°.∵AE 是角平 分线，∴∠CAE＝∠BAE＝38°，∴∠DAC＝∠DAE＋∠CAE＝56°，∴∠C＝90°－∠DAC＝34° 18．(9 分)已知等腰三角形的周长为 18 cm，其中两边之差为 3 cm，求三角形的各边长． 解：设腰长为 x cm，底边长为 y cm，则 2x＋y＝18， x－y＝3 或 2x＋y＝18， y－x＝3， 解得 x＝7， y＝4 或 x＝5， y＝8， 经检验，均能构成三角形，即三角形的三边长是 7 cm，7 cm，4 cm 或 5 cm，5 cm， 8 cm 19．(9 分)(淄博中考)已知：如图，△ABC 是任意一个三角形，求证：∠A＋∠B＋∠C ＝180°. 解： 如图，过点 A 作 EF∥BC，∵EF∥BC，∴∠1＝∠B，∠2＝∠C，∵∠1＋∠2＋∠BAC＝180°， ∴∠BAC＋∠B＋∠C＝180°，即∠A＋∠B＋∠C＝180° 20．(9 分)多边形的内角和与某一个外角的度数和为 1350 度． (1)求多边形的边数； (2)此多边形必有一内角为多少度？ 4 解：(1)设边数为 n，这个外角为 x°，则 0n B．m

查看更多