- 2021-04-28 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小学数学精讲教案4_2_7 格点型面积 教师版
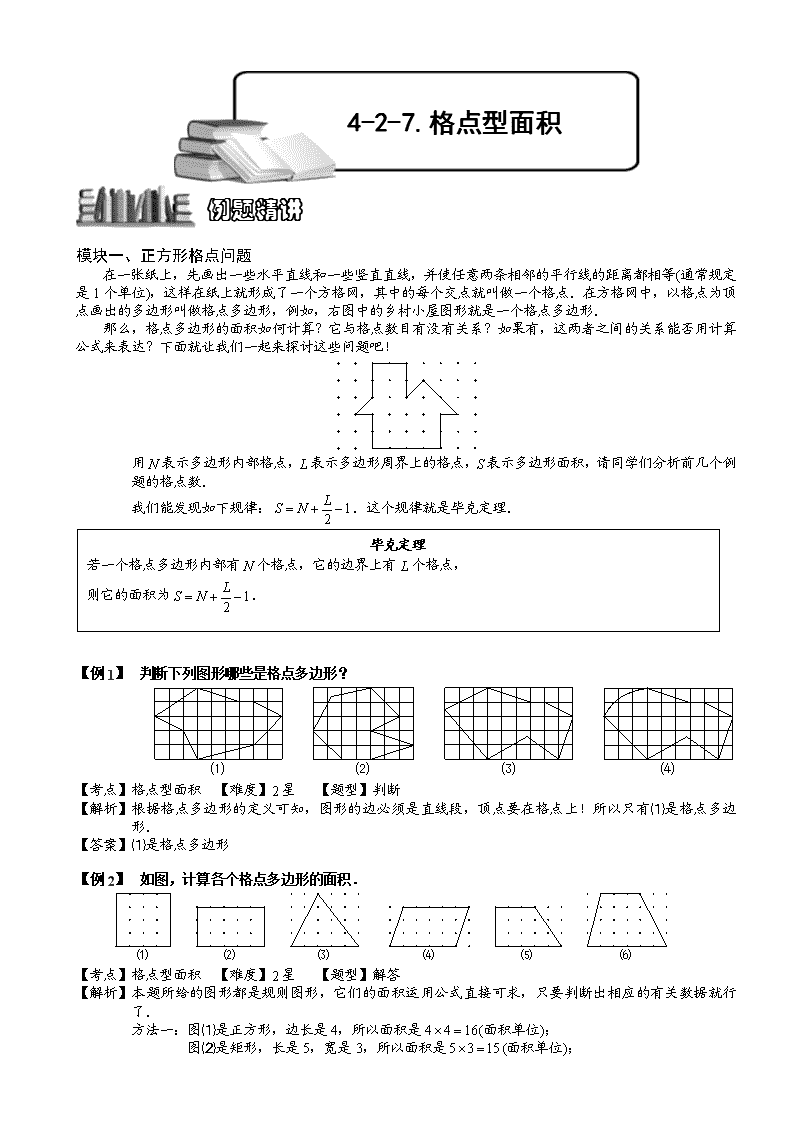
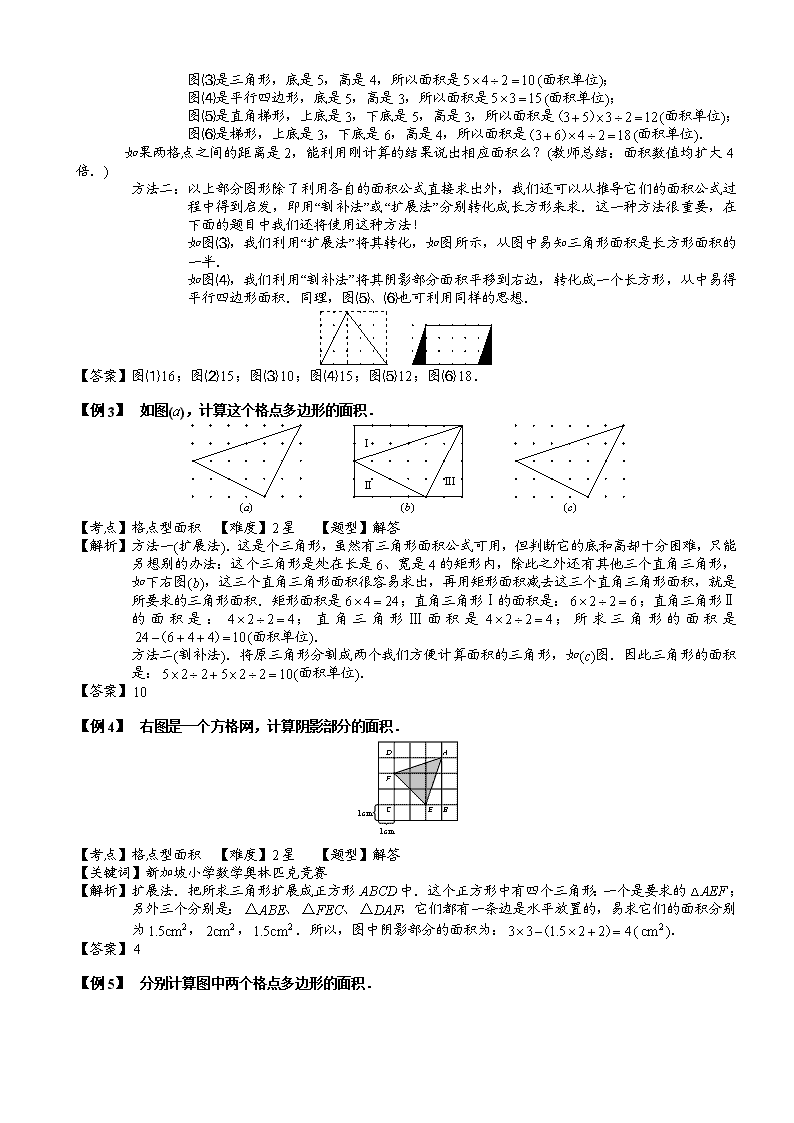
模块一、正方形格点问题 在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定 是 1 个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶 点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形. 那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算 公式来表达?下面就让我们一起来探讨这些问题吧! 用 N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例 题的格点数. 我们能发现如下规律: .这个规律就是毕克定理. 【例 1】 判断下列图形哪些是格点多边形? 【考点】格点型面积 【难度】2 星 【题型】判断 【解析】根据格点多边形的定义可知,图形的边必须是直线段,顶点要在格点上!所以只有⑴是格点多边 形. 【答案】⑴是格点多边形 【例 2】 如图,计算各个格点多边形的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断出相应的有关数据就行 了. 方法一:图⑴是正方形,边长是 4,所以面积是 (面积单位); 图⑵是矩形,长是 5,宽是 3,所以面积是 (面积单位); ⑴ ⑵ ⑶ ⑷ ⑶⑵⑴ ⑹⑸⑷ 4-2-7.格点型面积 例题精讲 12 LS N= + − 毕克定理 若一个格点多边形内部有 N 个格点,它的边界上有 L 个格点, 则它的面积为 12 LS N= + − . 4 4 16× = 5 3 15× = 图⑶是三角形,底是 5,高是 4,所以面积是 (面积单位); 图⑷是平行四边形,底是 5,高是 3,所以面积是 (面积单位); 图⑸是直角梯形,上底是 3,下底是 5,高是 3,所以面积是 (面积单位); 图⑹是梯形,上底是 3,下底是 6,高是 4,所以面积是 (面积单位). 如果两格点之间的距离是 2,能利用刚计算的结果说出相应面积么?(教师总结:面积数值均扩大 4 倍.) 方法二:以上部分图形除了利用各自的面积公式直接求出外,我们还可以从推导它们的面积公式过 程中得到启发,即用“割补法”或“扩展法”分别转化成长方形来求.这一种方法很重要,在 下面的题目中我们还将使用这种方法! 如图⑶,我们利用“扩展法”将其转化,如图所示,从图中易知三角形面积是长方形面积的 一半. 如图⑷,我们利用“割补法”将其阴影部分面积平移到右边,转化成一个长方形,从中易得 平行四边形面积.同理,图⑸、⑹也可利用同样的思想. 【答案】图⑴ ;图⑵ ;图⑶ ;图⑷ ;图⑸ ;图⑹ . 【例 3】 如图(a),计算这个格点多边形的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】方法一(扩展法).这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能 另想别的办法:这个三角形是处在长是 6、宽是 4 的矩形内,除此之外还有其他三个直角三角形, 如下右图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是 所要求的三角形面积.矩形面积是 ;直角三角形Ⅰ的面积是: ;直角三角形Ⅱ 的面积是: ;直角三角形Ⅲ面积是 ;所求三角形的面积是 (面积单位). 方法二(割补法).将原三角形分割成两个我们方便计算面积的三角形,如(c)图.因此三角形的面积 是: (面积单位). 【答案】 【例 4】 右图是一个方格网,计算阴影部分的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 【关键词】新加坡小学数学奥林匹克竞赛 【解析】扩展法.把所求三角形扩展成正方形 ABCD 中.这个正方形中有四个三角形:一个是要求的 ; 另外三个分别是: ABE、 FEC、 DAF,它们都有一条边是水平放置的,易求它们的面积分别 为 , , .所以,图中阴影部分的面积为: ( ). 【答案】 【例 5】 分别计算图中两个格点多边形的面积. IIIII I (c)(b)(a) 1cm 1cm A BC D E F 5 4 2 10× ÷ = 5 3 15× = 3 5 3 2 12+ × ÷ =( ) 3 6 4 2 18+ × ÷ =( ) 16 15 10 15 12 18 6 4 24× = 6 2 2 6× ÷ = 4 2 2 4× ÷ = 4 2 2 4× ÷ = 24 6 4 4 10− + + =( ) 5 2 2 5 2 2 10× ÷ + × ÷ = 10 AEF △ △ △ 21.5cm 22cm 21.5cm 3 3 1.5 2 2 4× − × + =( ) 2cm 4 【考点】格点型面积 【难度】3 星 【题型】解答 【解析】利用“扩展法”和“割补法”我们都可以简单的得到第一幅图的面积均为 9 面积单位.第二幅图的面积 均为 10 面积单位. 【点评】“一个格点多边形面积的大小很可能是由哪些因素决定呢?”“格点多边形内部的格点数和周界上的格 点数与格点多边形的面积有没有什么内在联系呢?”下面我们就来探讨一下! 在巩固中,我们发现两个图形面积相等.进一步还可以发现第一个图形边界上的格点数是 8 个;第 二个图形边界上的格点数是 10 个,包含在图形内的格点数也相等,都是 6 个. 【答案】第一幅图的面积均为 9;第二幅图的面积均为 10. 【巩固】求下列各个格点多边形的面积. 【考点】格点型面积 【难度】3 星 【题型】解答 【解析】⑴ ∵ ; ,∴ (面积单位); ⑵ ∵ ; ,∴ (面积单位); ⑶ ∵ ; ,∴ (面积单位); ⑷ ∵ ; ,∴ (面积单位). 用 N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例 题的格点数. 我们能发现如下规律: .这个规律就是毕克定理. 【答案】⑴ ;⑵ ;⑶ ;⑷ 【例 6】 “乡村小屋”的面积是多少? 【考点】格点型面积 【难度】3 星 【题型】解答 【解析】图形内部格点数 ;图形边界上的格点数 ;根据毕克定理, 则 (单位面 积). 【答案】 【例 7】 右图是一个 面积单位的图形.求矩形内的箭形 的面积. (1) (2) (3) (4) 12L = 10N = 121 10 1 152 2 LS N= + − = + − = 10L = 16N = 101 16 1 202 2 LS N= + − = + − = 6L = 12N = 61 12 1 142 2 LS N= + − = + − = 10L = 13N = 101 13 1 172 2 LS N= + − = + − = 12 LS N= + − 15 20 14 17 9N = 20L = 1 182 LS N= + − = 18 8 12× ABCDEFGH 【考点】格点型面积 【难度】3 星 【题型】解答 【解析】箭形 的面积 (面积单位). 【答案】 【例 8】 比较图中的两个阴影部分①和②的面积,它们的大小关系______ 【考点】格点型面积 【难度】3 星 【题型】填空 【关键词】希望杯,五年级,二试,第 9 题,6 分 【解析】①的面积为: ,②的面积也为 。所以两块阴影部分面积相 等均为 3。 【答案】相等 【例 9】 右图中每个小正方形的面积都是 1,那么图中这只“狗”所占的面积是多少? 【考点】格点型面积 【难度】4 星 【题型】解答 【解析】图形内部格点数为 54,图形周界上格点数为 19. 所以图形的面积为: (面积单位). 【答案】 【巩固】如图,每一个小方格的面积都是 1 平方厘米,那么用粗线围成的图形的面积是多少平方厘米? 【考点】格点型面积 【难度】3 星 【题型】解答 【解析】方法一:正方形格点阵中多边形面积公式:(N+ -1)×单位正方形面积,其中 N 为图形内格点数,L 为图形周界上格点数. 有 N=4,L=7,则用粗线围成图形的面积为:(4+ -1)×1=6.5(平方厘米) 方法二:如右上图,先求出粗实线外格点内的图形的面积, 有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形, 所以粗实线外格点内的图形面积为 1.5+l+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为 16,所以粗线围成的图形的面积为:16-9.5=6.5 平方厘米. 【答案】 平方厘米 H G F E DC B A ②① ④ ③② ① ⑤ ⑥ ABCDEFGH 8 10 2 1 4 8 4 2 1 2 12 32 2 46= + ÷ − + × + ÷ − × = + + =( ) ( ) 46 1 1 12 1 1 1 3 1 32 2 2 × × + × × + × × = 3 2 2 3× ÷ = 54 19 2 1 62.5+ ÷ − = 62.5 L 2 7 2 6.5 【例 10】 第一届保良局亚洲区城市小学数学邀请赛在 7 月 21 日开幕,下面的图形中,每一个小方格的面积 是 1,那么 7、2、1 三个数字所占的面积之和是多少? 【考点】格点型面积 【难度】3 星 【题型】解答 【关键词】保良局亚洲区城市小学数学竞赛 【解析】要计算三个数字所占的面积之和,可以先分别求出每个数字所占的面积.显然,图中的三个数字都 可以看作格点多边形,根据毕克定理,可以很方便地求出每个数字所占的面积.值得注意的是:数 字“7”内部有两个格点,而数字“2”和“1”内部都没有格点. 7 所 占 的 面 积 为 : ; 2 所 占 的 面 积 为 : ; 1 所 占 的 面 积 为 : .所以,这三个数字所占的面积之和为: . 【答案】 【例 11】 的方格纸,小方格的面积是 1 平方厘米,小方格的顶点称为格点.请你在图上选 7 个格点, 要求其中任意 3 个格点都不在一条直线上,并且使这 7 个点用直线连接后所围成的面积尽可能 大.那么,所围图形的面积是 平方厘米. 【考点】格点型面积 【难度】3 星 【题型】填空 【关键词】小学数学奥林匹克 【解析】为了使这 7 个点围成最大的面积,这 7 个点应尽量在正方形的边或顶点上,如图选取 7 个点,围成 面积最大.最大面积为 (平方厘米). 【答案】 平方厘米 【例 12】 两个边长相等的正方形各被分成 25 个大小相同的小方格.现将这两个正方形的一部分重叠起来, 若左上角的阴影部分(块状)面积为 ,右下角的阴影部分(线状)面积为 ,求大正方形 的面积. 【考点】格点型面积 【难度】5 星 【题型】解答 【关键词】从小爱数学 【解析】块状部分与线状部分之间的部分称为 D,则 D 与前者共 14 个方格,与后者共 17 个方格,因此每个 方格的面积是 大正方形的面积为 . 【答案】 平方厘米 【例 13】 将边长为正整数 的正方形平均分成 个小正方形,每个小正方形的顶点称为格点。例如:图 A 中的格点是边长为 的正方形的格点。图 B 中,在边长为 12 的正方形中有四个完全相同的直角三 角形。如果三角形的一条直角边是 3,那么这四个三角形各边共经过多少个格点?(每个格点只计 n 2n 2 15 2 1 8.5+ ÷ − = 24 2 1 11÷ − = 17 2 1 7.5÷ − = 8.5 11 7.5 27+ + = 27 5 5× 5 5 0.5 3 23.5× − × = 23.5 25.12cm 27.4cm 2197.4 5.12 17 14 cm25 − ÷ − =( )( ) ( ) 219cm 19 2 一次) 【考点】格点型面积 【难度】2 星 【题型】解答 【关键词】希望杯,四年级,二试,第 19 题,10 分 【解析】如下图是一个三角形的示意图,共经过了 33 个格点 【答案】 个格点 模块二、三角形格点问题 1、定义:所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的 面积为 1,以这样的点为顶点画出的多边形为三角形格点多边形. 2、公式:关于三角形格点多边形的面积同样有它的计算公式:如果用 S 表示面积,N 表示图形内包含的格点 数,L 表示图形周界上的格点数,那么有 ,就是格点多边形面积等于图形内部所包含格点数 的 2 倍与周界上格点数的和减去 2. 【例 14】 如图(a),有 21 个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形 ABC 的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】方法一:如图(b)所示,在 ABC 内连接相邻的三个点成 DEF,再连接 DC、EA、FB 后是 ABC 可看成是由 DEF 分别延长 FD、DE、EF 边一倍、一倍、二倍而成的,由等积变换不难得 到 , , ,所以 (面积单位). 方法二:如图(c)所示,作辅助线把图Ⅰ′、Ⅱ′、Ⅲ′分别移拼到Ⅰ、Ⅱ、Ⅲ的位置,这样可以通过数 小正三角形的方法,求出 ABC 的面积为 10. 方法三:如图(d)所示:作辅助线可知:平行四边形 ARBE 中有 6 个小正三角形,而 ABE 的面积是 平行四边形 ARBE 面积的一半,即 ,平行四边形 ADCH 中有 4 个小正三角形,而 ADC 的面积是平行四边形 ADCH 面积的一半,即 .平行四边形 FBGC 中有 8 个小正三角形,而 FBC 的面积是平行四边形 FBGC 的一半,即: .所以 (面积单位). 【答案】 【巩固】如图,每相邻三个点所形成的三角形都是面积为 1 的等边三角形,计算 ABC 的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 (A) (B) A B CDF E C B A (b)(a) ' ' 'Ⅰ Ⅱ Ⅲ H G R Ⅲ Ⅱ Ⅰ (c) (d) A B C E F D C B A C B A 33 2 2S N L= × + − 2ACDS = 3AEBS = 4FBCS = 1 2 3 4 10S = + + + = 3AEBS = 2ACDS = 4FBCS = 1 2 3 4 10S = + + + = 10 △ 【解析】因为 ; :所以 (面积单位). 【答案】 【例 15】 求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为 1 的等边三角形). 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】⑴ ∵ ; ,∴ (面积单位); ⑵ ∵ ; ,∴ (面积单位); ⑶ ∵ ; ,∴ (面积单位); ⑷ ∵ ; ,∴ (面积单位). 【答案】(1) ;(2) ;() 【例 16】 把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是 128,求图中粗线 所围成的三角形的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】图中有 (个)小三角形,那么一个小三角形的面积是 , 图形内部格点数为 12,图形周界上格点数为 4; 图形的面积为: (面积单位),进而得图形的面积为: . 【答案】 【例 17】 如图,如果每一个小三角形的面积是 1 平方厘米,那么四边形 ABCD 的面积是多少平方厘米? 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x 单位正三角形面积,其中 N 为图形内格点 数,L 为图形周界上格点数. 有 N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米). 法二:如下图,我们先数出粗实线内完整的小正三角形有 10 个,而将不完整的小正三角形分成 4 部 分计算,其中①部分对应的平行四边形面积为 4,所以①部分的面积为 2,②、③、④部分对应的 平行四边形面积分别为 2,8,6,所以②、③、④部分的面积分别为 1,4,3.所以粗实线内图形 的面积为 10+2+1+4+3=20(平方厘米). 【答案】 平方厘米 【例 18】 如果下图中任意相邻的三个点构成的三角形面积都是 2 平方厘米.那么,三角形 ABC 的面积是 _____平方厘米. (1) (2) (3) (4) D C B A ④ ③ ② ① A B C D ① 5N = 3L = 2 2 2 5 3 2 11S N L= × + − = × + − = 11 7L = 7N = 2 2 2 7 7 2 19S N L= × + − = × + − = 5L = 8N = 2 2 2 8 5 2 19S N L= × + − = × + − = 6L = 7N = 2 2 2 7 6 2 18S N L= × + − = × + − = 7L = 8N = 2 2 2 8 7 2 21S N L= × + − = × + − = 19 19 1 3 5 7 9 11 13 15 64+ + + + + + + = 128 64 2÷ = 2 12 4 2 26× + − = 26 2 52× = 52 20 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】 【答案】 平方厘米 模块三、构造格点进行解题 【例 19】 图中正六边形 ABCDEF 的面积是 54,AP=2PF,CQ=2BQ,求阴影四边形 CEPQ 的面积. 【考点】格点型面积 【难度】2 星 【题型】解答 【关键词】华杯赛 【解析】如图,将正六边形 ABCDEF 等分为 54 个小正三角形.根据平行四边形对角线平分平行四边形面积, 面积 , 面积 ,四边形 ABQP 面积 .上述三块面积之和为 .因 此,阴影四边形 CEPQ 面积为 . 【答案】 【例 20】 正六边形 ABCDEF 的面积是 6 平方厘米.M 是 AB 中点,N 是 CD 中点,P 是 EF 中点.问:三角 形 MNP 的面积是多少平方厘米? 【考点】格点型面积 【难度】2 星 【题型】解答 【关键词】华杯赛 【解析】将正六边形分成六个面积为 1 平方厘米的正三角形,再取它们各边的中点将每个正三角形分为 4 个 小正三角形.于是正六边形 ABCDEF 被分成了 24 个小正三角形,每一个小正三角形的面积是 (平方厘米),三角形 MNP 由 9 个小正三角形所组成,所以三角形 MNP 的面积 (平方厘米). 【答案】 【例 21】 如图涂阴影部分的小正六角星形面积是 16 平方厘米,问:大正六角星形面积是多少平方厘米? 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】如图,涂阴影部分的小正六角星形可分成 12 个与三角形 PMN 全等(能完全重叠地放在一起)的小三 角形.而图中的大正六角星形除去小正六角星形后.有 6×4=24 个与三角形 PMN 全等的小三角形, O P N M ABC ABD BCD ACDS S S S∆ ∆ ∆ ∆= + + 2 12 2 12 2 9= × + × + × 66( )= 平方厘米 66 PEF△ 3= CDE△ 9= 11= 3 9 11 23+ + = 54 23 31− = 31 6 24 0.25÷ = 0.25 9 2.25= × = 2.25 所以大正六角星形的面是小正六角星形的 3 倍,即 48 平方厘米. 【答案】 平方厘米 【例 22】 把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形.再将这个 六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向外作更小的正三角形,这样 就得到图所示的图形.如果这个图形面积是 1,那么原来的正三角形面积是多少? 【考点】格点型面积 【难度】2 星 【题型】解答 【解析】方法一:如右图,我们将图 6-5 分成若干个大小、形状完全相同的小正三角形,由 40 块小正三角形 组成图 6-5,而由 27 块小正三角形组成了图中最大的正三角形.120 块小正三角形的面积为 1,所以 每块为 ,那么原来的正三角形由 81 块小正三角形组成,其面积显然为 . 方法二:如下图,我们把图 6-5 中的三角形分成 A、B、C 三种,设 A 形正三角形面积为“1”,则 B、 C 两种正三角形的面积依次为“ ”、“ ”.在图中: A 种、B 种、C 种正三角形的个数依次为 1,3,12,所以图 6-5 中图形的面积为 1+3× +12× = .所以有“1”对应 ,而原来的正三角形即为三角形 A,所以原来的正三角形的面积为 . 【答案】 B A C 48 1 120 27 40 1 9 1 81 1 9 1 81 40 27 27 40 27 40 27 40查看更多