人教版九年级上册数学同步课件-第22章-22二次函数y=ax2+bx+c的 图象和性质
22.1.4 二次函数y=ax2+bx+c的
图象和性质
第二十二章 二次函数
第1课时 二次函数y=ax2+bx+c的图象和性质
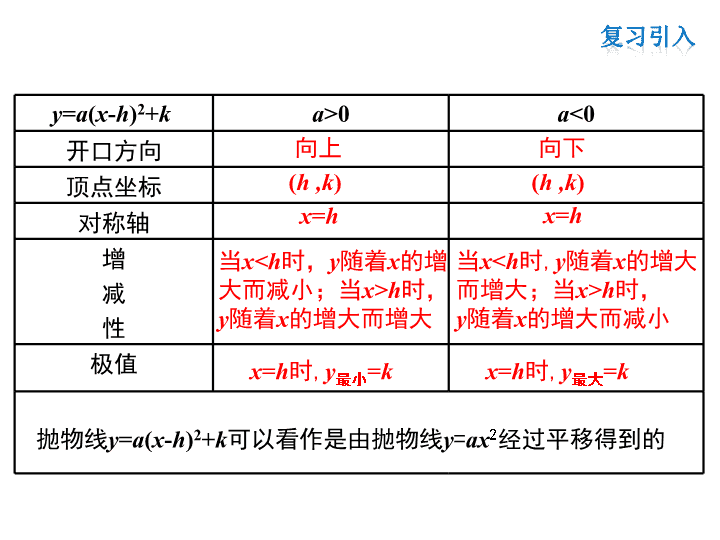
y=a(x-h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
向上 向下
(h ,k) (h ,k)
x=h x=h
当x
h时,
y随着x的增大而增大
当xh时,
y随着x的增大而减小
x=h时,y最小=k x=h时,y最大=k
抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的
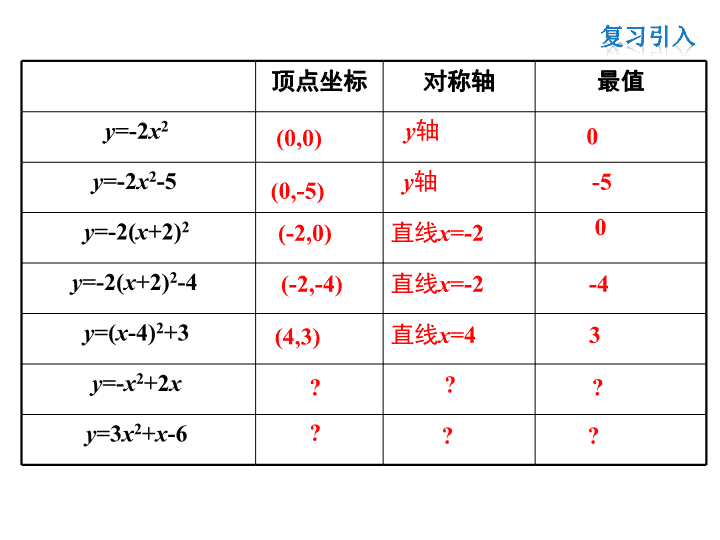
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0) y轴 0
(0,-5) y轴 -5
(-2,0) 直线x=-2 0
(-2,-4) 直线x=-2 -4
(4,3) 直线x=4 3
? ? ?
? ? ?
探究归纳
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些
知识来讨论 的图象和性质?21 6 212y x x
问题1 怎样将 化成y=a(x-h)2+k的形式?21 6 212y x x
二次函数y=ax2+bx+c的图象和性质1
21 6 212y x x 配方可得
2 2 21 ( 12 6 6 42)2 x x
21 ( 12 42)2 x x
2 2 21 [( 12 6 ) 6 42]2 x x
21 [( 6) 6]2 x 想一想:配方的方法及
步骤是什么?
21 ( 6) 3.2 x
问题2: 二次函数 可以看作是由
怎样平移得到的?
21 ( 6) 32y x 21
2y x
答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
问题3: 你能说出 的对称轴及顶点坐标吗?21 ( 6) 32y x
答:对称轴是直线x=6,顶点坐标是(6,3).
问题4: 如何用描点法画二次函数 的图象?21 6 212y x x
…
…
…
…9876543x
解: 先利用图形的对称性列表
21( 6) 32y x 7.5 5 3.5 3 3.5 5 7.5
5 10 x
y
5
10然后描点画图,得到图象如右图.
O
问题5 :结合二次函数 的图象,说出其性
质.
21 6 212y x x
5 10 x
y
5
10
x=6
解:当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
试一试
你能用上面的方法讨论二次函数y=-2x2-4x+1的图象和性质吗?
O
想一想:
我们如何用配方法将一般式y=ax2+bx+c(a≠0)
化成顶点式y=a(x-h)2+k?
将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k2
y=ax²+bx+c ca
b
a
bxa
bxa
22
2
22
2 2
2
2 2
b b ba x x ca a a
ca
b
a
bxa
42
22
2 24 .2 4
b a c ba x a a
★二次函数y=ax2+bx+c的图象和性质
2
2 2 4( ) .2 4
b ac by ax bx c a x a a
24( , ).2 4
b ac b
a a
2
bx a
,
★二次函数y=ax2+bx+c的图象和性质
(1) (2)
x
y
O x
y
O
如果a>0,当x< 时,y随x的
增大而减小;当x> 时,
y随x的增大而增大.
如果a<0,当x< 时,y随x
的增大而增大;当x> 时,
y随x的增大而减小.
2
bx a
2
bx a
2
b
a
2
b
a
2
b
a
2
b
a
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的
增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴
右侧,y的值随x值的增大而减小.由题设可知,当x>1时,y的值
随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线
x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即
b≤1,故选择D .
2
2 ( 1)
bx b
D
例1
练一练
填表:
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1) x=1 最大值1
(0,-1) y轴 最大值-1
最小值-6( ,-6)1
3
直线x= 1
3
D
由图象上横坐标为 x=-2的点在第三象限可得4a-
2b+c<0,故③正确;
由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二
象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a
+c)2<b2,故④正确.
解析:由图象开口向下可得a<0,由对称轴在y轴左侧可得b
<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故
①正确;
由对称轴x>-1可得2a-b<0,故②正确;
二次函数y=ax2+bx+c的图象与系数a、b、c的关系1
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其
中正确的个数是 ( )
A.1 B.2 C.3 D.4
例2
★二次函数y=ax2+bx+c的图象与系数a、b、c的关系
①a决定开口方向:a>0⇔开口向上;a<0⇔开口向下;
②a、b同号对称轴在y轴的左侧;
a、b异号对称轴在y轴的右侧;
③c=0⇔经过原点;
c>0⇔与y轴的交点位于x轴的上方;
c<0⇔与y轴的交点位于x轴的下方;
④当x=1时,y的值为a+b+c;
当x=-1时,y的值为a-b+c.
⑤当对称轴x=1时,x= =1,∴-b=2a,此时2a+b=0;
当对称轴x=-1时,x= =-1,∴b=2a,此时2a-b=0.
因此,判断2a+b的符号,需判断对称轴x= 与1的大小,
若对称轴在直线x=1的左边,则 ,再根据a的符号即可得
出结果;判断2a-b的符号,同理需判断对称轴与1的大小.
a
b
2
a
b
2
a
b
2
< 12
b
a
-
1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A.y轴 B.直线x=
C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )D
5
2
3
2
2.根据公式确定下列二次函数图象的对称轴和顶点坐标:
2
2
(1) 2 12 13;
(2) 5 80 319;
1(3) 2 2 ;2
(4) 1 2 .
y x x
y x x
y x x
y x x
直线x=3 3, 5
直线x=8 8, 1
直线x=1.25
5 9, 4 8
直线x= 0.5 1 9, 2 4
3.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,
有下列结论:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若
(-3,y1),( ,y2)是抛物线上两点,则y1>y2.其中正确的是
( )
2
3
A.①②③ B.①③④
C.①②④ D.②③④
x
y
O 2
x=-1
B
O
y
x
–1
–2
3
4.已知二次函数y=ax2+bx+c(a≠0)的图
象如图所示,则下列结论:
(1)a、b同号;
(2)当x=–1和x=3时,函数值相等;
(3) 4a+b=0;
(4)当y=–2时,x的值只能取0;
其中正确的是 .
直线x=1
(2)
24( , )2 4
b ac b
a a
2
bx a
y=ax2+bx+c(a ≠0)
(一般式) (顶点式)
2
2 4( )2 4
b ac by a x a a