- 2021-04-28 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年湖北省沙市中学高二下学期第一次半月考数学(文)试题(Word版)无答案
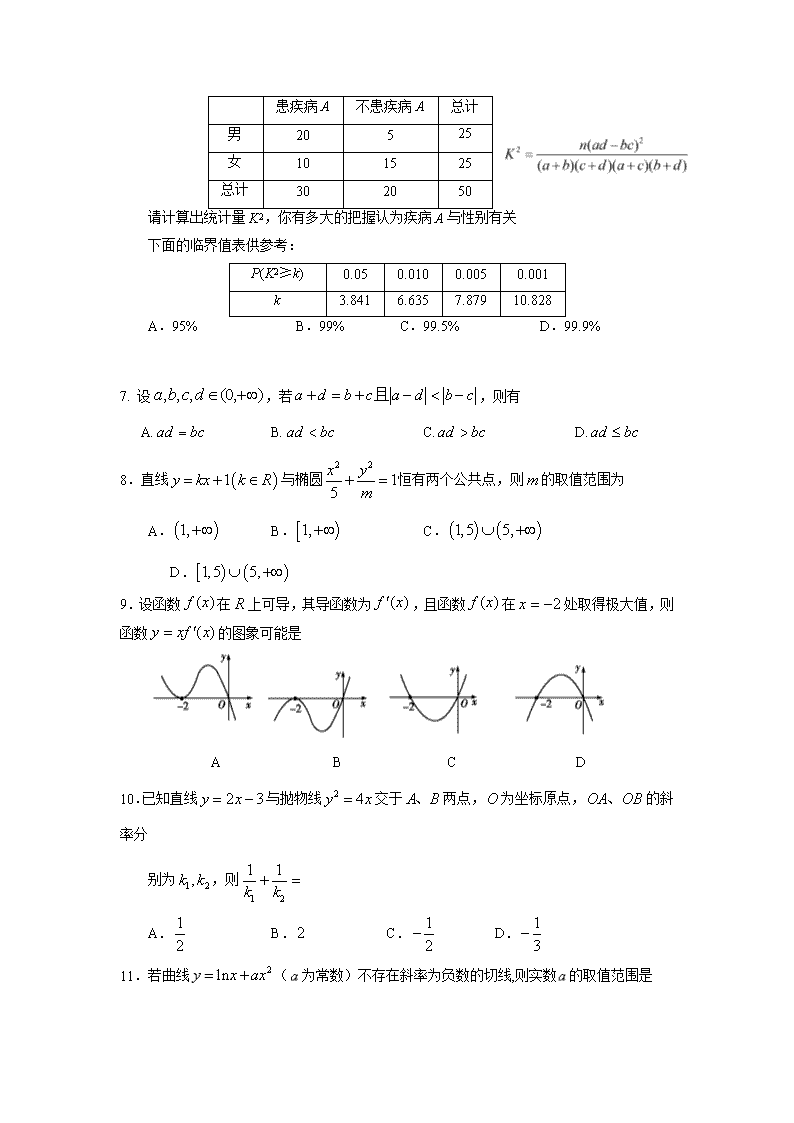
2017-2018学年湖北省沙市中学高二下学期第一次半月考文科数学试卷 考试时间:2018年3月15日 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确的答案填涂在答题卡上. 1.双曲线的渐近线方程为 A. B. C. D. 2.命题“”是命题“”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 3.命题“若x,y都是偶数,则x+y也是偶数“的逆否命题是 A.若x+y是偶数,则x与y不都是偶数 B.若x+y是偶数,则x与y都不是偶数 C.若x+y不是偶数,则x与y不都是偶数D.若x+y不是偶数,则x与y都不是偶数 4. 下列说法中错误的是 A.在频率分布直方图中,中位数左边和右边的直方图的面积相等. B.一个样本的方差是,则这组数据的总和等 于60. C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越差.] D.对于命题使得<0,则,使. 5.掷一枚均匀的硬币4次,出现正面的次数多于反面的次数的概率为 A. B. C. D. 6.为了解疾病A是否与性别有关,在一医院随机地对入院的50人进行了问卷调查得到了如下 的列联表: 患疾病A 不患疾病A 总计 男 20 5 25 女 10 15 25 总计 30 20 50 请计算出统计量K2,你有多大的把握认为疾病A与性别有关 下面的临界值表供参考: P(K2≥k) 0.05 0.010 0.005 0.001 k 3.841 6.635 7.879 10.828 A.95% B.99% C.99.5% D.99.9% 7. 设,若,则有 A. B. C. D. 8.直线与椭圆恒有两个公共点,则的取值范围为 A. B. C. D. 9.设函数在上可导,其导函数为,且函数在处取得极大值,则函数的图象可能是 A B C D 10.已知直线与抛物线交于两点,为坐标原点,的斜率分 别为,则 A. B. C. D. 11.若曲线(为常数)不存在斜率为负数的切线,则实数的取值范围是 A. B. C. D. 12. 若函数,当时,恒成立,则的取值范围 A. B. C. D. 二、填空题:本大题共4个小题,每小题5分,共20分。请将答案填在答题卡对应题号的位置 上,答错位置,书写不清,模棱两可均不得分。 13.某单位有200名职工,现要用系统抽样法从中抽取40名职工作样本,将全体职工随机按1~ 200编号,并按编号顺序平均分成40组 (1~5号,6~10号,…,196~200号).若第5组 抽出的号码为22,则第8组抽出的号码应是__________. 14.设f0(x)=sin x,f1(x)=f′0(x),f2(x)=f′1(x),……,fn+1(x)=f′n(x),n∈N,则f2 018(x)= . 15.若在区间内随机取一个数,在区间内随机取一个数,则使方程 有两个不相等的实根的概率为 . 16.我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至 于不能割,则与圆合体而无所失矣”它体现了一种无限与有限转化过程.比如在表达式 中“”即代表无限次重复,但原式却是个定值,它可以通过方程求 得,类似上述过程,则_____________. 三、解答题:本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤。 17.(本小题满分10分)已知命题: “是焦点在轴上的椭圆的标准方程”; :“函数在上存在极值”;若命题“且”是假命题,“或” 是真命题,求实数的取值范围. 18. (本小题满分12分) 已知 (1)当时,求曲线在点处的切线方程; (2)求当时,求的极值. 19.(本小题满分12分) x 1 2 3 4 5 y 58 54 39 29 10 菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水(单位:千克)清洗该蔬菜千克后,蔬菜上残留的农药(单位:微克)的统计表: (1)在坐标系中描出散点图,并判断变量与的相关性; (2)若用解析式作为蔬菜农药残量与用水量的回 归方程,令,计算平均值和,完成以下表格(填在 答题卡中),求出与的回归方程.(精确到0.1) (3)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时 1 4 9 16 25 y 58 54 39 29 10 对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千 克蔬菜?(精确到0. 1,参考数) (附:线性回归方程计算 公式:,) 20. (本题满分12分) 某商场销售某种商品的经验表明,该商品每日的销售量(单位:千克)与销售价格(单位: 元/千克)满足关系式,其中,为常数.已知销售价格为4 元/千克时,每日可售出该商品10.5千克. (1)求的值; (2)若该商品的成本为2元/千克,试确定销售价格的值,使商场每日销售该商品所获得 的利润最大. 21.(本小题满分12分) 已知椭圆的离心率,左、右焦点分别为,点 ,点在线段的中垂线上. (1)求椭圆的方程; (2)设直线与椭圆交于两点,直线与的倾斜角分别为, 且,求证:直线过定点,并求该定点的坐标. 22.(本小题满分12分) 设函数 (1)讨论函数的单调性; (2)若有两个极值点,记过点的直线的斜率为, 问:是否存在实数,使得,若存在,求出的值;若不存在,请说明理由.查看更多