- 2021-04-28 发布 |
- 37.5 KB |
- 48页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级上册数学拓展课件-第1单元 长方体和正方体-苏教版(共48张PPT)
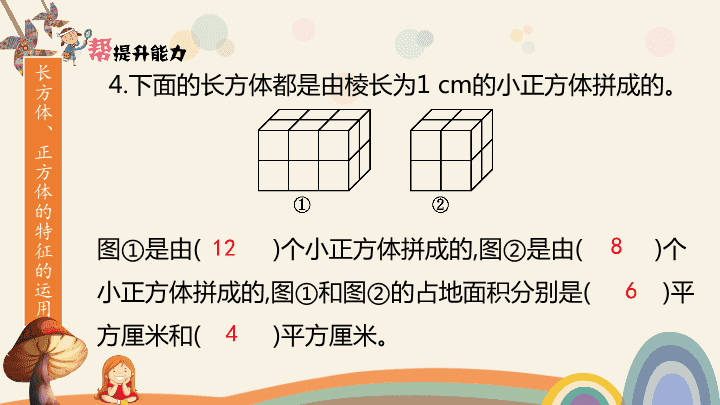
小学提升拓展课件 江苏版六年级上 第 1 课时 长方体和正方体的认识 图①是由 ( ) 个小正方体拼成的 , 图②是由 ( ) 个 小正方体拼成的 , 图①和图②的占地面积分别是 ( ) 平 方厘米和 ( ) 平方厘米。 长方体、正方体的特征的运用 4. 下面的长方体都是由棱长为 1 cm 的小正方体拼成的。 12 8 6 4 5. 有一个底面是边长为 4 厘米的正方形的长方体 , 高是 15 厘米 , 这个长方体的棱长和是多少厘米 ? (15+4+4) ×4=92( 厘米) 答:这个长方体的棱长和是 92 厘米。 长方体、正方体棱长和的计算及运用 6. 用两根同样长的铁丝分别做一个长方体和正方体框架 , 长方体长、宽、高分别为 8 厘米 ,4 厘米 ,6 厘米 , 正方体框架的棱长是多少厘米 ? ( 8+4+6 ) ×4=72 (厘米) 72 ÷12=6 (厘米) 答:正方体框架的棱长是 6 厘米。 第 2 课时 长方体和正方体的展开图 ( ) ( ) ( ) 长方体和正方体展开图的判定 4. 下面哪些图形能折成长方体 ? 能折成长方体的打“√” , 不能折成长方体的打“✕”。 √ ✕ √ 5. 下面哪些图形能折成正方体 ? 能折成正方体的打“√” , 不能折成正方体的打“✕”。 √ ✕ ✕ √ √ ✕ 6. 下面两幅图是张爷爷用铁皮做的长方体、正方体容器展开图的一部分 , 请你画出每幅图剩余的面 , 使它们成为一个完整的展开图。 长方体、正方体棱长和的计算及运用 7. 下面能围成一个长 4 cm, 宽 3 cm, 高 2 cm 的长方体的是 ( )( 填序号 ) 。 1456578 第 3 课时 长方体和正方体的表面积( 1 ) 4. 中秋节到了 , 君君给爷爷准备了一份礼物 , 礼物的盒子是棱长为 0.5 分米的正方体 , 他要包装这个礼品盒至少要用多少平方分米的包装纸 ?( 接口粘贴处不算 ) 0.5×0.5×6=1.5 (平方分米) 答:包装这个礼盒至少要用 1.5 平方分米的包装纸。 利用长方体、正方体表面 积的计算方法解决问题 5. 某一种汽车的油箱 , 长 4 分米 , 宽和高都是 2.5 分米 , 如果用铁皮来做这个油箱 , 至少要用多少铁皮 ? ( 4×2.5+2.5×2.5+4×2.5 ) ×2=52.5 (平方分米) 6. 一个魔方的表面积是 54 平方厘米 , 它的一个面的面积是多少平方厘米 ? 它的棱长是多少厘米 ? 54÷6=9 (平方厘米) 3×3=9 (厘米) 答:它的一个面的面积是 9 平方厘米。棱长是 9 厘米。 第 4 课时 长方体和正方体的表面积( 2 ) 9. 奥运会标准游泳池长 50 米 , 宽 21 米 , 深 2.5 米 , 要在游泳池的底部和四周覆盖防水涂层。至少要准备多少平方米的防水涂层 ? (50×2.5+21×2.5) × 2+50 × 21=1405 (平方米) 答:至少要准备 1405 平方米的防水涂层。 联系实际、解决问题 10. 国家游泳中心又被称为“水立方” , 它的墙面和屋顶外部都包裹着“ ETFE 膜” ,“ 水立方”是当今世界上规模最大 , 构造最复杂 , 技术最全面的 ETFE 建筑 ,“ 水立方”的长为 177 米 , 宽为 177 米 , 高为 30 米 ,“ 水立方”的外部至少需要“ ETFE 膜”多少平方米 ? 177×177+ ( 177×30+177×30 ) ×2=52569 (平方米) 答:水立方”的外部至少需要“ ETFE 膜” 52569 平方米。 11. 张老师家客厅的长是 6 米 , 宽是 4 米 , 高是 3 米 , 门窗面积共 8 平方米。要粉刷四周墙壁和屋顶 , 粉刷的面积是多少平方米 ? 如果每平方米用涂料 1.5 千克 , 那么一共要用涂料多少千克 ? ( 6 × 3+4 × 3 ) ×2+6 ×4-8=76 (平方米) 76 ×1.5=114 (千克)答:一共要用涂料 114 千克。 12. 一个长方体的长、宽、高都扩大到原来的 3 倍 , 这个长方体的表面积扩大为原来的 ( ) 倍。 9 长方体长、宽、高及正 方体棱长变化巩固运用 13. 一个大正方体的表面积是小正方体表面积的 4 倍 , 那么大正方体的棱长是小正方体棱长的 ( ) 倍 . 2 14. 有一个正方体木块 , 把它分成两个长方体后 , 表面积增加了 24 平方厘米 , 这个正方体木块原来的表面积是多少平方厘米 ? 24÷2×6=72 (平方厘米) 答:这个正方体木块原来的表面积是 72 平方厘米 . 长方体或正方体切割 拼合后的表面积问题 15. 一个长方体木块 , 被锯下一个小长方体木块后 , 剩余部分的表面积是多少平方厘米 ? ( 8×6+8×5+5×6 ) ×2=236 (平方厘米) 答:剩余部分的表面积是 236 平方厘米 . 第 5 课时 认识体积和容积 5. 我是小法官。 ( 对的打“√” , 错的打“✕” ) (1) 木箱的体积就是木箱的容积。 ( ) (2) 物体的体积越大 , 所占的空间就越大。 ( ) (3) 有一块橡皮泥 , 第一次把它捏成正方体 , 第二次把它捏成长方体 , 第三次把它捏成球形 , 这三次捏成的物体的体积一样大。 ( ) ✕ 体积和容积意义的运用 √ √ 6. 开心选一选。 (1) 烁烁用零花钱为爷爷买了足浴盆 , 足浴盆中的水 ( 爷爷泡脚时 ) 的体积与足浴盆容积的关系是 ( ) 。 A. 体积 > 容积 B. 体积 = 容积 C. 体积 < 容积 D. 不确定 (2)“ 求一个油桶能装油多少升”是求油桶的 ( ) 。 A. 表面积 B. 容积 C. 体积 D. 占地面积 C B 第 6 课时 体积单位 6. 我是小法官。 (1) 体积单位比面积单位大 , 面积单位比长度单位大 ( ) (2) 钢笔吸一次墨水 , 大约能吸 1 至 2 升墨水。 ( ) (3)1 立方米棉花和 1 立方米铁所占空间一样大。 ( ) (4) 盛满汤的碗 , 汤的体积就是碗的容积。 ( ) (5) 我国第一艘载人航天飞船“神舟五号”的返回舱的容积约是 6 立方分米。 ( ) ✕ 对体积单位或容积 单位的理解和运用 ✕ √ √ ✕ 7. 下面的玻璃缸中原来都盛有 500 mL 的水 , 在每个玻璃缸中都放入一个石头 , 结果如下图。每个石头的体积是多少立方厘米 ? 在括号里填一填。 300 375 体积、容积单位换算 252 8. 下面的物体都是由 1 立方厘米的小正方体摆成的 , 在括号里填出它们的体积。 17 13 观察物体计算体积 第 7 课时 长方体和正方体的体积( 1 ) 4. 计算下列长方体和正方体的体积。 运用公式计算体积 5×20×20=2000( 立方厘米) 3×3×3=27( 立方分米) 5. 人民英雄 , 永垂不朽。矗立在天安门广场的人民英雄纪念碑的碑心是一块长 14.7 米 , 宽 2.9 米 , 厚 1 米的长方体石材 , 它的体积是多少立方米 ? 14.7 ×2.9 ×1=42.63 (立方米) 答:它的体积是 42.63 立方米 . 运用体积计算公 式解决实际问题 6. 一个正方体的棱长总和是 108 cm, 它的体积是多少立方厘米 ? 108 ÷12=9 (厘米) 9 ×9 ×9=729 (立方厘米) 答:它的体积是 729 立方厘米 . 7. 填空。 (1) 一个长方体的长、宽、高都扩大到原来的 2 倍 , 它的表面积扩大到原来的 ( ) 倍 , 体积扩大到原来的 ( ) 倍。 (2) 一个正方体的棱长扩大到原来的 3 倍 , 它的表面积扩大到原来的 ( ) 倍 , 体积扩大到原来的 ( ) 倍。 4 长方体、正方体 体积计算的拓展 8 9 27 第 8 课时 长方体和正方体的体积( 2 ) 5. 一个长方体的药水箱里装了 60 升的药水 , 已知药水箱里面长 5 分米 , 宽 3 分米 , 药水的深是多少分米 ? 运用公式解决实际问题 60 ÷(5 × 3 ) =4( 分米) 答:药水的深是 4 分米 . 6. 用 5 厘米厚的泡沫做一个正方体的泡沫保温箱 , 该正方体保温箱的棱长是 40 厘米 , 该泡沫保温箱的体积和容积各是多少 ? 体积: 40 ×40 ×40=64000 (立方厘米) 容积: 40-5 ×2=30 (厘米) 30 ×30 ×30=27000 (立方厘米) 巧算体积与容积 第 9 课时 不规则物体的体积 5. 一个长方体容器 , 内部的长为 6 dm, 宽为 4 dm, 高为 8 dm 。把一个棱长是 2 dm 的正方体铁块浸没水中后 ( 水没有溢出 ), 水面升高了多少分米 ? 解决与不规则物 体体积相关的问题 2×2×2÷(6×4)= (dm) 答:水面升高了 dm 。 1 3 1 3 6. 一个长方体容器内部的长为 6 dm, 宽为 4 dm, 高为 6 dm, 容器内装满水 , 一个铁块浸没水中后一部分水溢出 , 再把铁块取出 , 这时长方体内水面高 4 dm, 这个铁块的体积是多少立方分米 ? 6×4×(6-4)=48(dm3) 答 : 这个铁块的体积是 48 dm3 。 第 10 课时 体积单位间的进率 8. 一个容积是 8000 L 的长方体水池 , 底面积是 40 m2, 水池深多少米 ? 体积与容积单 位换算的应用 8000 升 =8000 立方分米 =8 立方米 8÷40=0.2(m) 答 : 水池深 0.2 m 。 9. 一根长方体方钢 , 长是 2 米 , 横截面是边长为 6 厘米的正方形 , 这根方钢的体积是多少立方厘米 ? 如果每立方厘米的方钢重 7.8 克 , 那么这根方钢重多少千克 ? 2 米 =200 厘米 6×6×200=7200( 立方厘米 ) 7200×7.8=56160( 克 ) 56160 克 =56.16 千克 答 : 这根方钢重 56.16 千克。 表面涂色的正方体 3. 把棱长是 6 厘米的正方体表面涂色 , 分割成棱长是 1 厘米的小正方体 ,6 个面都不涂色的小正方体有多少个 ? 运用规律解决问题 6×6×6=216( 个 ) 216-8-12×(6-2)-6×(6-2)2=64( 个 ) 答 :6 个面都不涂色的小正方体有 64 个。 4. 把棱长是 5 厘米的正方体表面涂色 , 分割成棱长是 1 厘米的小正方体 , 至少有一面涂色的正方体有多少个 ? 8+12×(5-2)+6×(5-2)2=98( 个 ) 答 : 至少有一面涂色的正方体有 98 个。 5. 一个正方体 , 在它的每个面上都涂上红色 , 再把它平均切成棱长是 1 厘米的小正方体 , 已知两面涂色的小正方体有 96 个 , 求大正方体的棱长。 96÷12+2=10( 个 ) 10×1=10( 厘米 ) 答 : 大正方体的棱长为 10 厘米。 谢谢观赏 谢谢观赏 谢谢观赏查看更多