高考理科数学专题复习练习 3.1导数的概念及运算
第三章导数及其应用
3.1导数的概念及运算
专题2
导数的运算
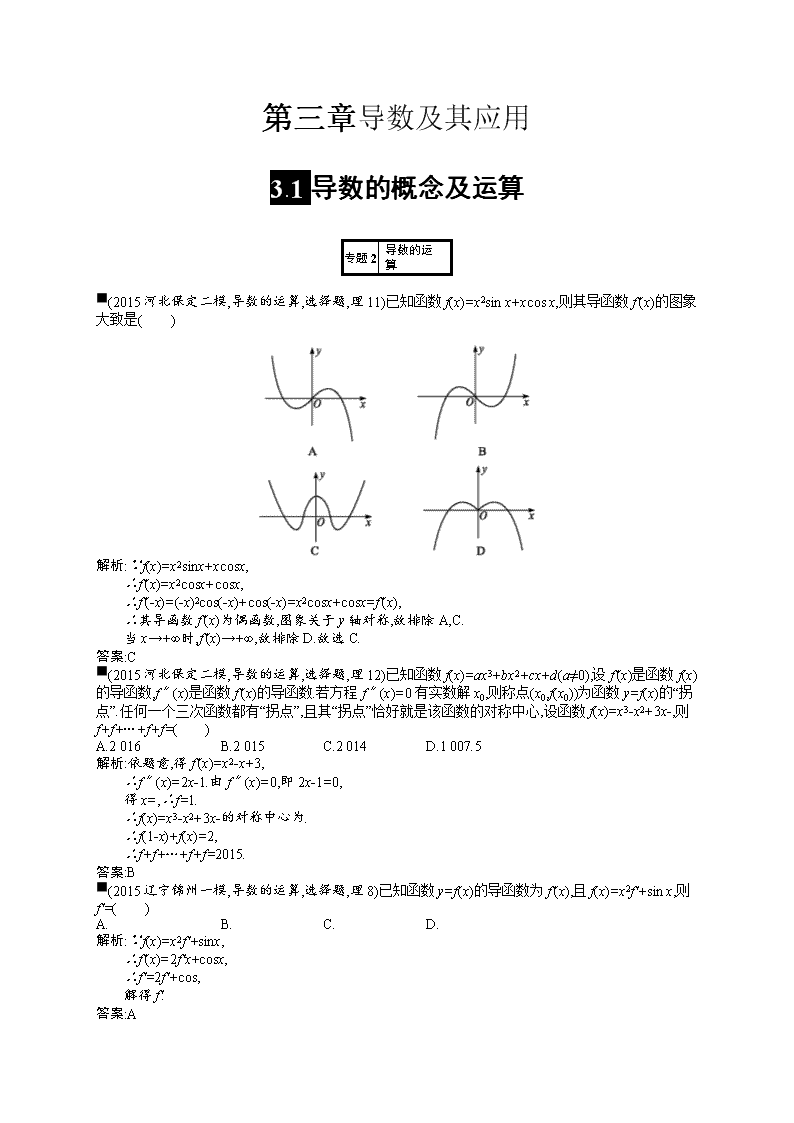
■(2015河北保定二模,导数的运算,选择题,理11)已知函数f(x)=x2sin x+xcos x,则其导函数f'(x)的图象大致是( )
解析:∵f(x)=x2sinx+xcosx,
∴f'(x)=x2cosx+cosx,
∴f'(-x)=(-x)2cos(-x)+cos(-x)=x2cosx+cosx=f'(x),
∴其导函数f'(x)为偶函数,图象关于y轴对称,故排除A,C.
当x→+∞时,f'(x)→+∞,故排除D.故选C.
答案:C
■(2015河北保定二模,导数的运算,选择题,理12)已知函数f(x)=ax3+bx2+cx+d(a≠0),设f'(x)是函数f(x)的导函数,f″(x)是函数f'(x)的导函数.若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.任何一个三次函数都有“拐点”,且其“拐点”恰好就是该函数的对称中心,设函数f(x)=x3-x2+3x-,则f+f+…+f+f=( )
A.2 016 B.2 015 C.2 014 D.1 007.5
解析:依题意,得f'(x)=x2-x+3,
∴f″(x)=2x-1.由f″(x)=0,即2x-1=0,
得x=,∴f=1.
∴f(x)=x3-x2+3x-的对称中心为.
∴f(1-x)+f(x)=2,
∴f+f+…+f+f=2015.
答案:B
■(2015辽宁锦州一模,导数的运算,选择题,理8)已知函数y=f(x)的导函数为f'(x),且f(x)=x2f'+sin x,则f'=( )
A. B. C. D.
解析:∵f(x)=x2f'+sinx,
∴f'(x)=2f'x+cosx,
∴f'=2f'+cos,
解得f'.
答案:A
3.2导数与函数的单调性、极值、最值
专题1
导数与函数的单调性
■(2015江西南昌三模,导数与函数的单调性,选择题,理10)已知f(x)=x3-ax在[1,+∞)上是单调增函数,则a的取值范围是( )
A.(3,+∞) B.(1,3)
C.(-∞,3) D.(-∞,3]
答案:D
■(2015河北邯郸二模,导数与函数的单调性,解答题,理21)已知函数f(x)=mln x-x2+(2m-1)x.(m∈R).
(1)讨论f(x)的单调性;
(2)设m>0,证明:当0
f(m-x);
(3)若函数f(x)的图象与x轴交于A,B两点,线段AB的中点的横坐标为x0,f'(x)为函数f(x)的导函数,证明f'(x0)<0.
解:(1)f(x)的定义域为(0,+∞),
∴f'(x)=-2x+2m-1=-.
当m≤0时,f(x)在(0,+∞)上单调递减;
当m>0时,若x∈(0,m),则f'(x)>0,f(x)单调递增;
若x∈(m,+∞),则f'(x)<0,f(x)单调递减.
(2)设t1=m+x,t2=m-x,则t1+t2=2m,t1-t2=2x,
∴f(t1)-f(t2)=mln-(t1-t2)(t1+t2)+(2m-1)(t1-t2)=mln-2x,
∴f(m+x)-f(m-x)=mln-2x.
设g(x)=mln-2x,
则g'(x)=,且m>0,00,g(x)在(0,m)上递增,
∴g(x)>g(0)=m>0,
∴f(m+x)>f(m-x).
(3)设A,B的横坐标分别为x1,x2,且x10,且0f(m-(m-x1))=f(x1)=f(x2)=0,
又∵f(x)在(m,+∞)上单调递减,
∴2m-x1f'(x)成立,则( )
A.3f(ln 2)<2f(ln 3)
B.3f(ln 2)=2f(ln 3)
C.3f(ln 2)>2f(ln 3)
D.3f(ln 2)与2f(ln 3)的大小不确定
解析:构造函数g(x)=,
∴g'(x)=[f'(x)-f(x)].
∵对任意x∈R都有f(x)>f'(x)成立,
∴g'(x)<0,即g(x)在R上单调递减.
又ln2g(ln3),
∴,
∴,
∴3f(ln2)>2f(ln3).
答案:C
■(2015辽宁锦州一模,导数与函数的单调性,选择题,理12)已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f'(x)g(x)>f(x)g'(x),且f(x)=ax·g(x)(a>0,且a≠1),,若数列的前n项和大于62,则n的最小值为( )
A.6 B.7 C.8 D.9
解析:∵f'(x)g(x)>f(x)g'(x),
∴f'(x)g(x)-f(x)g'(x)>0,
∴'=>0,
从而可得=ax单调递增,从而可得a>1.
∵=a+a-1=,
∴a=2.
故+…+=a+a2+…+an=2+22+…+2n==2n+1-2>62.
∴2n+1>64,即n+1>6,n>5,n∈N*.
∴n的最小值为6.
答案:A
专题3
导数与函数的最值
■(2015江西南昌三模,导数与函数的最值,选择题,理12)已知函数f(x)=aln(x+1)-x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式>1恒成立,则实数a的取值范围为( )
A.[15,+∞) B.(-∞,15] C.(12,30] D.(-12,15]
答案:A
■(2015江西南昌三模,导数与函数的最值,解答题,理21)已知函数f(x)=2ex-(x-a)2+3,a∈R.
(1)若函数y=f(x)的图象在x=0处的切线与x轴平行,求a的值;
(2)若x≥0,f(x)≥0恒成立,求a的取值范围.
解:(1)f'(x)=2(ex-x+a).
∵y=f(x)在x=0处的切线与x轴平行,即在x=0处切线斜率为0,即f'(0)=2(a+1)=0.
∴a=-1.
(2)f'(x)=2(ex-x+a),令g(x)=2(ex-x+a),则g'(x)=2(ex-1)≥0,
∴g(x)=2(ex-x+a)在[0,+∞)内单调递增,g(0)=2(1+a).
①当2(1+a)≥0,即a≥-1时,f'(x)=2(ex-x+a)≥f'(0)≥0,
f(x)在[0,+∞)内单调递增,要想f(x)≥0,只需要f(0)=5-a2≥0,
解得-≤a≤,从而-1≤a≤.
②当2(1+a)<0,即a<-1时,由g(x)=2(ex-x+a)在[0,+∞)内单调递增知,
存在唯一x0使得g(x0)=2(-x0+a)=0,有=x0-a,令f'(x)>0,解得x>x0,令f'(x)<0,解得0≤x-3)上的最小值;
(3)若对∀x≥-2,kf(x)≥g(x)恒成立,求实数k的取值范围.
解:(1)f'(x)=aex(x+2),g'(x)=2x+b.
由题意,两函数在x=0处有相同的切线.
∴f'(0)=2a,g'(0)=b,
∴2a=b,f(0)=a=g(0)=2,∴a=2,b=4,
∴f(x)=2ex(x+1),g(x)=x2+4x+2.
(2)f'(x)=2ex(x+2),由f'(x)>0得x>-2,由f'(x)<0得x<-2,
∴f(x)在(-2,+∞)上单调递增,在(-∞,-2)上单调递减.
∵t>-3,∴t+1>-2.
①当-30得ex>,
∴x>ln;由F'(x)<0得xe2时,F(x)在[-2,+∞)单调递增,F(x)min=F(-2)=-2ke-2+2=(e2-k)<0,不满足F(x)min≥0.
②当ln=-2,即k=e2时,由①知,F(x)min=F(-2)=(e2-k)=0,
满足F(x)min≥0.
③当ln>-2,即1≤k0,
满足F(x)min≥0.
综上所述,满足题意的k的取值范围为[1,e2].
3.3导数的综合应用
专题2
利用导数研究函数的零点或方程的根
■(2015河北保定二模,利用导数研究函数的零点或方程的根,解答题,理21)设函数f(x)=mln x+.
(1)若m≤0,求函数f(x)的单调区间;
(2)若函数f(x)在(0,2)内存在两个极值点,求m的取值范围.
解:(1)函数f(x)的定义域为(0,+∞),
f'(x)=.
当m≤0时,mx-ex<0,
所以当00,f(x)单调递增;
x>2时,f'(x)<0,f(x)单调递减.
综上:f(x)的单调递增区间为(0,2),单调递减区间为(2,+∞).
(2)若m≤0时,由(1)知,函数f(x)在(0,2)内单调递增,故f(x)在(0,2)内不存在极值点;
当m>0时,设函数g(x)=mx-ex(x∈(0,2)).
因为g'(x)=m-ex,
①当00,f(x)单调递增,
故f(x)在(0,2)内不存在两个极值点.
②当m>1时,x∈(0,lnm)时,g'(x)>0,函数y=g(x)单调递增,x∈(lnm,+∞)时,g'(x)<0,函数y=g(x)单调递减,
∴函数y=g(x)的最大值为g(lnm)=m(lnm-1).
函数f(x)在(0,2)内存在两个极值点.
当且仅当解得e0,即函数g(x)在(0,1]上为增函数,此时在(0,1]上没有交点,不满足条件.
若c<0,
当g(x)与f(x)在(0,1]上相切时,由g'(x)=得3x2+c=,即3x2=-c,由x3+cx=(x-1)两个方程联立得c=-,x=,即切点坐标为.当g(x)与f(x)不相切时,即c≠-时,要使在(0,1]上,两个函数只有一个交点,则满足g(1)<0,
即1+c<0,解得c<-1.
综上c=-或c<-1.
答案:c=-或c<-1
■(2015辽宁锦州二模,利用导数研究函数的零点或方程的根,解答题,理21)已知函数f(x)=ln(ax+1)+x3-x2-ax.
(1)若x=为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(3)若a=-1使方程f(1-x)-(1-x)3=有实根,求实数b的取值范围.
解:(1)f'(x)=+3x2-2x-a=,
∵x=为f(x)的极值点,∴f'=0,
∴3a(3-2a)-(a2+2)=0且a+1≠0,解得a=0.
又当a=0时,f'(x)=x(3x-2),从而x=为f(x)的极值点成立.
(2)∵f(x)在[1,+∞)上为增函数,
∴≥0在[1,+∞)上恒成立.
若a=0,则f'(x)=x(3x-2),此时f(x)在[1,+∞)上为增函数成立,故a=0符合题意.
若a≠0,由ax+1>0对x>1恒成立知a>0.
所以3ax2+(3-2a)x-(a2+2)≥0对x∈[1,+∞)上恒成立.
令g(x)=3ax2+(3-2a)x-(a2+2),其对称轴为x=.
∵a>0,∴,从而g(x)在[1,+∞)上为增函数.
∴只要g(1)≥0即可,即-a2+a+1≥0成立,
解得≤a≤.
又a>0,∴00上有解.
即求函数g(x)=xlnx+x2-x3的值域.
方法一:b=x(lnx+x-x2),令h(x)=lnx+x-x2.
由h'(x)=+1-2x=.
∵x>0,∴当00,
从而h(x)在(0,1)上为增函数;
当x>1时,h'(x)<0,从而h(x)在(1,+∞)上为减函数.
∴h(x)≤h(1)=0,而h(x)可以无穷小.∴b的取值范围为(-∞,0].
方法二:g'(x)=lnx+1+2x-3x2,g″(x)=+2-6x=-.
当00,
∴g'(x)在上递增;
当x>时,g″(x)<0,
∴g'(x)在上递减.
又g'(1)=0,∴令g'(x0)=0,00,
∴g(x)在x01时,g'(x)<0,
∴g(x)在x>1上递减.
又当x→+∞时,g(x)→-∞,g(x)=xlnx+x2-x3=x(lnx+x-x2)≤x.
当x→0时,lnx+<0,则g(x)<0,且g(1)=0,
∴b的取值范围为(-∞,0].
专题3
利用导数解决不等式的有关问题
■(2015江西宜春奉新一中高考模拟,利用导数解决不等式的有关问题,解答题,理21)函数f(x)=x2+mln(x+1).
(1)若函数f(x)是定义域上的单调函数,求实数m的取值范围;
(2)若m=-1,试比较当x∈(0,+∞)时,f(x)与x3的大小;
(3)证明:对任意的正整数n,不等式e0+e-1×4+e-2×9+…+成立.
解:(1)根据题意,由f'(x)=2x+,
可知f'(x)≥0或f'(x)≤0在(-1,+∞)上恒成立.
下面分两种情况讨论:
①当f'(x)=≥0在(-1,+∞)上恒成立时,
有m≥-2x2-2x=-2在(-1,+∞)上恒成立,故m≥;
②当f'(x)=≤0在(-1,+∞)上恒成立时,
有m≤-2x2-2x=-2在(-1,+∞)上恒成立.
∵-2在(-1,+∞)上没有最小值,
∴不存在实数m使f'(x)<0在(-1,+∞)上恒成立.
综上所述,实数m的取值范围是.
(2)当m=-1时,即函数f(x)=x2-ln(x+1).
令g(x)=f(x)-x3=-x3+x2-ln(x+1),
则g'(x)=-3x2+2x-=-.
显然,当x∈(0,+∞)时,g'(x)<0,即函数g(x)在(0,+∞)上单调递减;
又g(0)=0,所以当x∈(0,+∞)时,恒有g(x)1时,f(x)的图象恒在直线l的上方,求k的最大值.
解:(1)∵f'(x)=1+lnx,
∴f'(e)=1+lne=k-3.
∴k=5.
(2)由于存在x0∈[1,e],使f(x0)x0lnx0,∴a>.设h(x)=,
则h'(x)=.
当x∈[1,e]时,h'(x)≥0(仅当x=e时取等号).
∴h(x)在[1,e]上单调递增,
∴h(x)min=h(1)=0,因此a>0.
(3)由题意xlnx>(k-3)x-k+2在x>1时恒成立,
即k<.设F(x)=,
∴F'(x)=.
令m(x)=x-lnx-2,则m'(x)=1->0在x>1时恒成立.
∴m(x)在(1,+∞)上单调递增,且m(3)=1-ln3<0,m(4)=2-ln4>0.
∴在(1,+∞)上存在唯一实数x0(x0∈(3,4))使m(x)=0.
当1x0时,m(x)>0,即F'(x)>0.
∴F(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增.
∴F(x)min=F(x0)==x0+2∈(5,6).
故kx2+4-2x-8.
解:(1)f'(x)=ex+a,
由已知,f'(0)=-1,f(0)=-1,
故a=-2,b=-2,
所以f'(x)=ex-2.
当x∈(-∞,ln2)时,f'(x)<0,当x∈(ln2,+∞)时,f'(x)>0,
故f(x)在(-∞,ln2)单调递减,在(ln2,+∞)单调递增.
(2)当x≥0时,2≤(x+1)+1=x+2,
所以x2+4-2x-8≤x2+2(x+2)-2x-8=x2-4,
设g(x)=f(x)-(x2-4)=ex-x2-2x+2,
g'(x)=ex-2x-2.
因为g'(0)=-1<0,g'(2)=e2-4>0,00,
即g(x)在[0,x0)单调递减,在(x0,+∞)单调递增.
当x≥0时,g(x)≥g(x0)=-2x0+2=4->0,
即f(x)>x2-4,
因此f(x)>x2+4-2x-8.
■(2015辽宁丹东一模,利用导数解决不等式的有关问题,解答题,理21)已知x=1是函数f(x)=1+(1-x)ln(kx)的极值点,e为自然对数的底数.
(1)求k的值,并讨论f(x)的单调性;
(2)是否存在m∈(1,+∞),使得当a>m时,不等式(a+x)ln(a+x)0.
当x∈(1,+∞)时,f'(x)=g(x)<0,
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
(2)不等式(a+x)ln(a+x)0,f(e)=2-e<0,
∴h'(x)在(0,1)和(1,+∞)上各有一个零点,分别设为x1和x2,列表:
x
(0,x1)
x1
(x1,x2)
x2
(x2,+∞)
h'(x)
-
0
+
0
-
h(x)
↙
极小值
↗
极大值
↙
∴h(x)在(x1,x2)是增函数,在(x2,+∞)是减函数.
∵x2∈(1,+∞),
∴存在这样的m值,且m=x2.
■(2015辽宁葫芦岛二模,利用导数解决不等式的有关问题,解答题,理21)已知函数f(x)=aln x+x2+x,g(x)=x2+(a+1)x+;
(1)若f(x)在(1,f(1))处的切线方程为x+y+b=0,求a,b的值;
(2)是否存在实数a使得f(x)在(0,+∞)上单调递减,g(x)在上单调递增,若存在,求出a的值,若不存在,请说明理由;
(3)令H(x)=f(x+1)-g(x),若x1,x2(x10,G(-1)>0,解得0x1.
∵H(x2)=aln(x2+1)+=-2(x2+1)x2ln(x2+1)+
x1=(-1-x2),
∴只需证明:-2(x2+1)x2ln(x2+1)+(-1-x2),
即:-2(x2+1)x2ln(x2+1)+x2>-ln2.①
令φ(x)=x2-2(x+1)xln(x+1)+x,x∈,
φ'(x)=2x-2(2x+1)ln(x+1)-2x+ln2-=-2(2x+1)ln(x+1)+ln2-.
∵-0.∴-2(2x+1)ln(x+1)>0.
又∵ln2-=ln2-ln=ln>0,
∴φ'(x)>0,
∴φ(x)在上单调递增.
∴φ(x)>φln2-ln2+-ln2,
即φ(x)>-ln2,即①式成立.
∴H(x2)>x1.
综上x1
查看更多