- 2021-04-28 发布 |
- 37.5 KB |
- 14页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版六年级下册数学教学课件-第6单元 整理和复习 1-第9课时 比和比例(2)
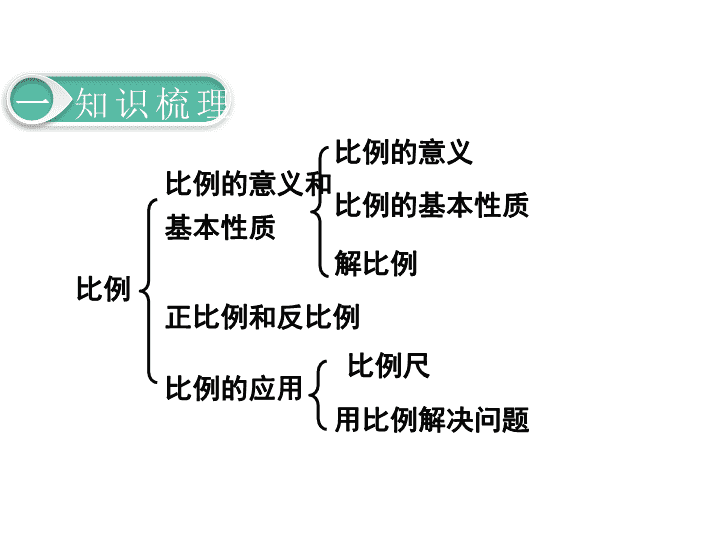
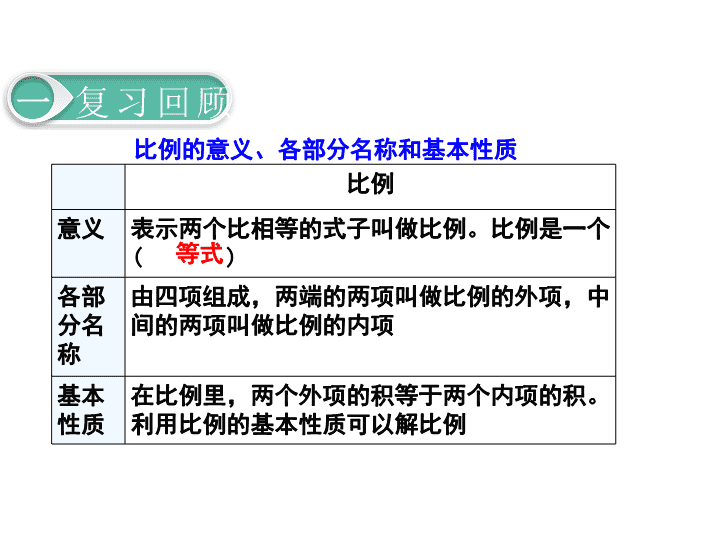
1. 数与代数 第9课时 比和比例(2) 比例 一 知识梳理 比例的意义 和基本性质 正比例和反比例 比例的意义 比例的基本性质 解比例 比例的应用 比例尺 用比例解决问题 比例 意义 表示两个比相等的式子叫做比例。比例是一 个( ) 各部 分名 称 由四项组成,两端的两项叫做比例的外项, 中间的两项叫做比例的内项 基本 性质 在比例里,两个外项的积等于两个内项的积。 利用比例的基本性质可以解比例 等式 比例的意义、各部分名称和基本性质 一 复习回顾 正比例和反比例的概念 正比例:两种相关联的量,其中一种量增加,另 一种量也随着增加,一种量减少,另一种量也随 着减少;两种量的比值一定。 一 复习回顾 正比例和反比例的概念 反比例:两种相关联的量中,其中一种量增加, 另一种量反而减少,一种量减少,另一种量反而 增加;两种量的积一定。 一 复习回顾 变化规律 图像 正 比 例 两种量同时扩大、同 时缩小 表示正比例关系的图象 是一条由点(0,0)引出 的( ) 反 比 例 一种量扩大(或缩小), 另一种量反而缩小(或 扩大) 表示反比例关系的图象 是( ) 直线 曲线 正比例和反比例的变化规律 一 复习回顾 判断两种相关联的量成正比例关系或反比例关系的方法: (1)分析这两种相关联的量,看它们是相( )的 关系还是相( )的关系; (2)再看它们是比值一定还是积一定,如果相比,比值 一定,那么就成( )比例关系;如果相乘,积一 定,那么就成( )比例关系。 比 正 反 乘 一 复习回顾 比例尺 一幅地图的( )与( ) 的比,叫做这幅地图的比例尺,即图上距 离∶实际距离=比例尺。比例尺分为( ) 比例尺和( )比例尺。 图上距离=( ); 图上距离 实际距离 线段 数值 实际距离×比例尺 图上距离 比例尺 二 巩固练习 实际距离=( )。 1.判断下列各题中两种量是否成比例,若成比 例,请指出成什么比例关系? ①单价一定,总价和数量。 ②正方体的棱长和它的体积。 ③路程一定,速度和时间。 ④圆的周长和直径。 ⑤圆的面积和半径。 正比例关系 不成比例 反比例关系 正比例关系 不成比例 二 巩固练习 (1)长度一定的绳子,平均分成若干段,每段的长 度和分的段数成( )比例关系。 (2)如果 = ,那么a和b成( )比例关系。 (3)一个长方形的长是8 cm,它的面积和宽成 ( )比例关系。 a b 1 2 反 正 正 2.填空。 二 巩固练习 (3)从甲地到乙地,丽丽用15分钟,平平用12分钟, 丽丽和平平的速度比是( )。 (4)一个长方体的棱长总和是64cm,长、宽、高的 比是4∶3∶1,这个长方体的体积是( )cm3。 (5)在比例尺是1∶5000000的地图上,图上距离 3cm表示实际距离( )km。 4:5 96 150 二 巩固练习 二 巩固练习 答:氢有0.6kg,氧有 4.8kg。 答:302块金牌需要黄金1812克。 二 巩固练习 答:北京到济南全程需要5.375 小时。 答:甲、丙两地的实际距离 是960千米。 二 巩固练习 活动后,又骑车1小时 活动后,又骑车1小时返回原地查看更多