人教版8年级上册数学全册课时13_4课题学习导学案

人教版8年级上册数学全册课时13_4课题学习导学案

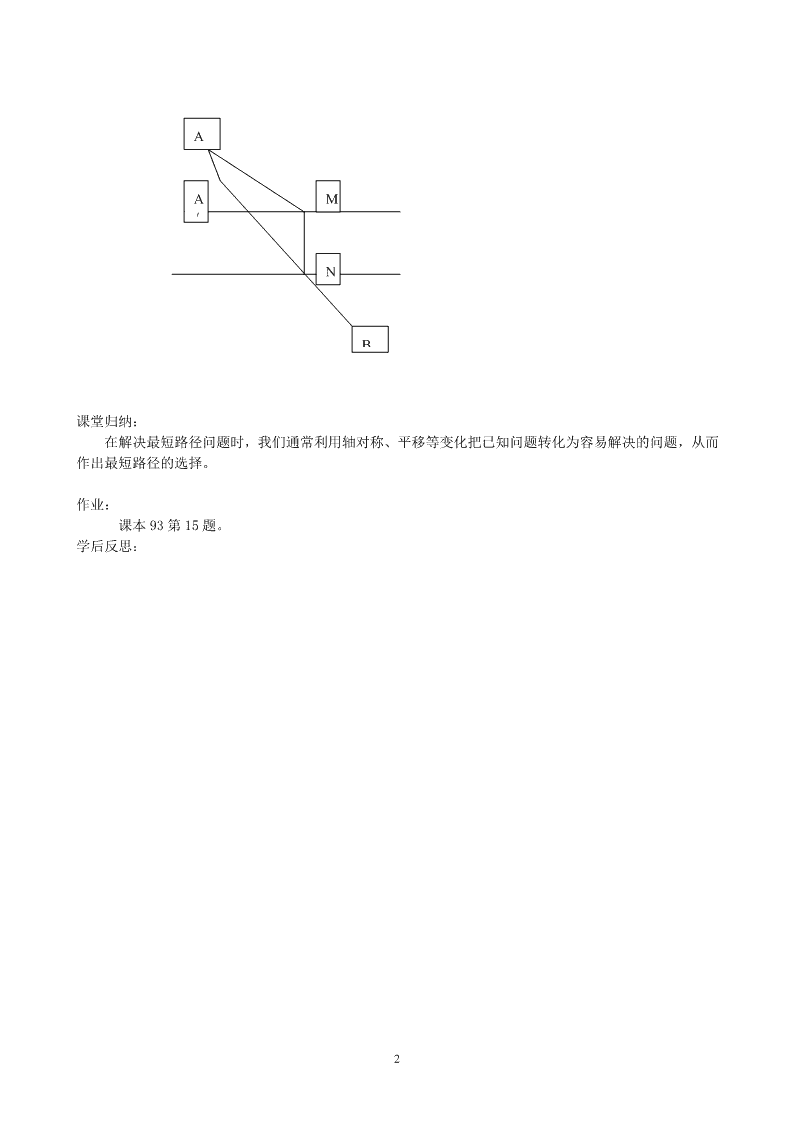
1 13.4 课题学习 最短路径问题导学案 【学习目标】 1， 复习轴对称的知识，会画轴对称图形。 2， 能够利用轴对称的知识解决实际问题。 3， 培养同学们自学意思和探究能力。 学习重点：会画轴对称图形。 学习难点：会用轴对称知识解决实际问题。 一、复习导入： （1），同学们以前学过的线段最短问题有哪些？还记得吗？ 1、 2、 （2），如何做直线外一点关于这条直线的对称点？ 1、 2、 二、导入新课 问题 1 如图牧马人从 A 地出发，到一条笔直的河边 L 饮马，然后到 B 地。牧马人到河边什么地方饮马， 可使所走的路径最短？ 作点 A 或 B 关于直线 L 的对称点 B′或 A′，再连接 AB′或 BA′与对称轴 L 的交点即为所求。 （证明方法为：三角形两边之和大于第三边） 问题 2 如图，A 和 B 两地在一条河的两岸，现要在河上造一座桥 MN，桥造成在何处可使从 A 到 B 的路 径 AMNB 最短？（假定河的两岸是平行的直线，桥要与河垂直） 分析引导：我们可以把河岸看成两条平行线，N 为直线 b 上一个动点，MN 垂直于直线 b，交直线 a 于 点 M,这样问题可以转化成：当点 N 在直线 b 的什么位置时 AM+MN+NB 最小。 解：将 AM 沿与河岸垂直的方向平移，点 M 移动到点 N，点 A 移动到点 A′,则 AA′=MN,AM+NB=A′N+NB. 连接 A′，B 两点的线中，线段 A′B 最短。因此线段 A′B 与直线 b 的交点 N 的位置即为所求。 能 力 提 升 ： 你 能 证 明 为 什 么 点 N 即 为 所 求 的 点 吗 ？ A B L 2 课堂归纳： 在解决最短路径问题时，我们通常利用轴对称、平移等变化把已知问题转化为容易解决的问题，从而 作出最短路径的选择。 作业： 课本 93 第 15 题。 学后反思： A B A ′ N M