2017-2018学年湖南省双峰县第一中学高二12月月考数学（理）试题

2017-2018学年湖南省双峰县第一中学高二12月月考数学（理）试题

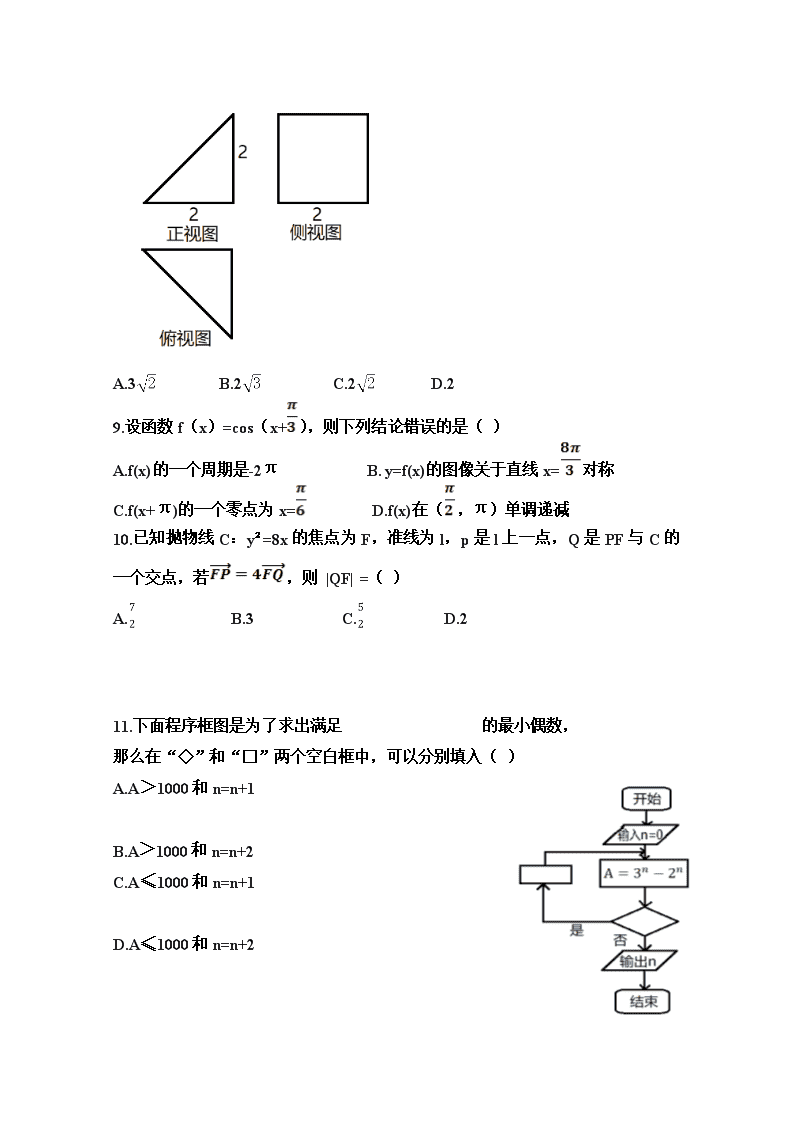
‎2017-2018学年湖南省双峰县第一中学高二12月月考数学(理科)试卷 一、选择题（每小题5分，共60分）‎ ‎1.已知集合A={x|x<1}，B={x|<1}，则（ ）‎ A. A∩B={x|x<0} B. A∪B=R C. A∪B={x|x>1} D. A∩B=Φ ‎2.设函数f（x），g（x）的定义域为R，且f（x）是奇函数，g（x）是偶函数，则（ ）‎ A. f（x）·g（x）是偶函数 B. |f（x）|·g（x）是奇函数 C. f（x）·|g（x）|是奇函数 D. |f（x）·g（x）|是奇函数 ‎3.已知向量= (1,m),=(3,-2),且(+)⊥，则m=（ ）‎ A. -8 B.-6 C.6 D.8‎ ‎4.设命题p:ョn∈N，n²＞，则¬p为（ ）‎ A. p:∀n∈N，n²＞ B. p:ョn∈N，n²≤‎ C. p:∀n∈N，n²≤ D.p:ョn∈N，n²=‎ ‎5.F为双曲线C：x²-my2=3m（m>0）的一个焦点，则点F到C的一条渐近线的距离为（ ）‎ A. B.3 C.m D.3m ‎6.设x、y满足条件则z=2x+y的最小值是（ ）‎ A.-15 B.-9 C.1 D.9‎ ‎7.设,则f（-2）+f（）=（ ）‎ A.3 B.6 C.9 D.12‎ ‎8.一四棱椎的三视图如图所示，则该四棱锥的最长棱的长为（ ）‎ ‎[‎ A.3 B.2 C.2 D.2‎ ‎9.设函数f（x）=cos（x+），则下列结论错误的是（ ）‎ A.f(x)的一个周期是-2π B. y=f(x)的图像关于直线x=对称 C.f(x+π)的一个零点为x= D.f(x)在（，π）单调递减 ‎10.已知抛物线C：y²=8x的焦点为F，准线为l，p是l上一点，Q是PF与C的一个交点，若，则 |QF| =（ ）‎ A. B.3 C. D.2‎ ‎11.下面程序框图是为了求出满足的最小偶数，‎ 那么在“◇”和“□”两个空白框中，可以分别填入（ ）‎ A.A＞1000和n=n+1‎ B.A＞1000和n=n+2‎ C.A≤1000和n=n+1 ‎ ‎ ‎ D.A≤1000和n=n+2‎ ‎12.若x=-2是函数f（x）=(x²+ax-1)·的极值点，则f（x）的极小值为（ ）‎ A.-1 B.-2 C.5 D.1‎ 二、填空题（每小题5分，共20分）‎ ‎13.函数f（x）=（x∈[0,]）的最大值是 ‎ ‎14.α、β是两个平面，m、n是两条直线，有下列命题：‎ ‎①若m⊥n，m⊥α，n∥β，则α⊥β ‎②若m⊥α，n∥α，则m⊥n ‎③若α∥β，mα，则m∥β ‎④若m∥n，α∥β，则m与α所成角和n与β所成角相等，‎ 其中正确的命题序号是 ‎ ‎15.若a，b∈R，ab>0，则的最小值为 ‎ ‎16.过原点作曲线y=+16的切线，则切线方程为 ‎ 三、解答题（17题10分，18-22题每题12分，共70分）‎ ‎17已知p：>a；q：x²-2ax+1≤0的解集非空。若p∨q为真，p∧q为假，求a的取值范围 ‎18△ABC中，内角A，B，C的对边分别为a，b，c，已知2cosC(acosB+bcosA)=c ‎(1)求角C ‎(2)若c=，△ABC的面积为，求△ABC的周长 ‎19．Sn为数列{}前n项和，已知>0，²+2=4+3‎ ‎(1)求{}的通项公式 ‎(2)设=，求{}的前n项和 ‎20.如图，在四棱锥P-ABCD中，AB//CD,且∠BAP=∠CDP=90°‎ ‎(1)证明：平面PAB⊥平面PAD ‎(2)若PA=PD=AB=DC,∠APD=90°，求二面角A-PB-C余弦值 ‎21.椭圆C的一顶点为A(0，-1)，焦点在x轴上，其右焦点到直线x-y+2=0‎ 的距离为3‎ ‎(1)求椭圆的标准方程 ‎(2)若直线y=kx+m(k≠0)与椭圆C相交于M.N两点，且|AM|=|AN|,求m的取值范围 ‎22.已知f(x)=x²-2ax+lnx ‎(1)当a=1时，求f(x)的单调性 ‎(2)若f(x)有两个不同的极值点x1，x2(x1

查看更多