- 2021-04-28 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市初三中考数学二模汇编题几何证明
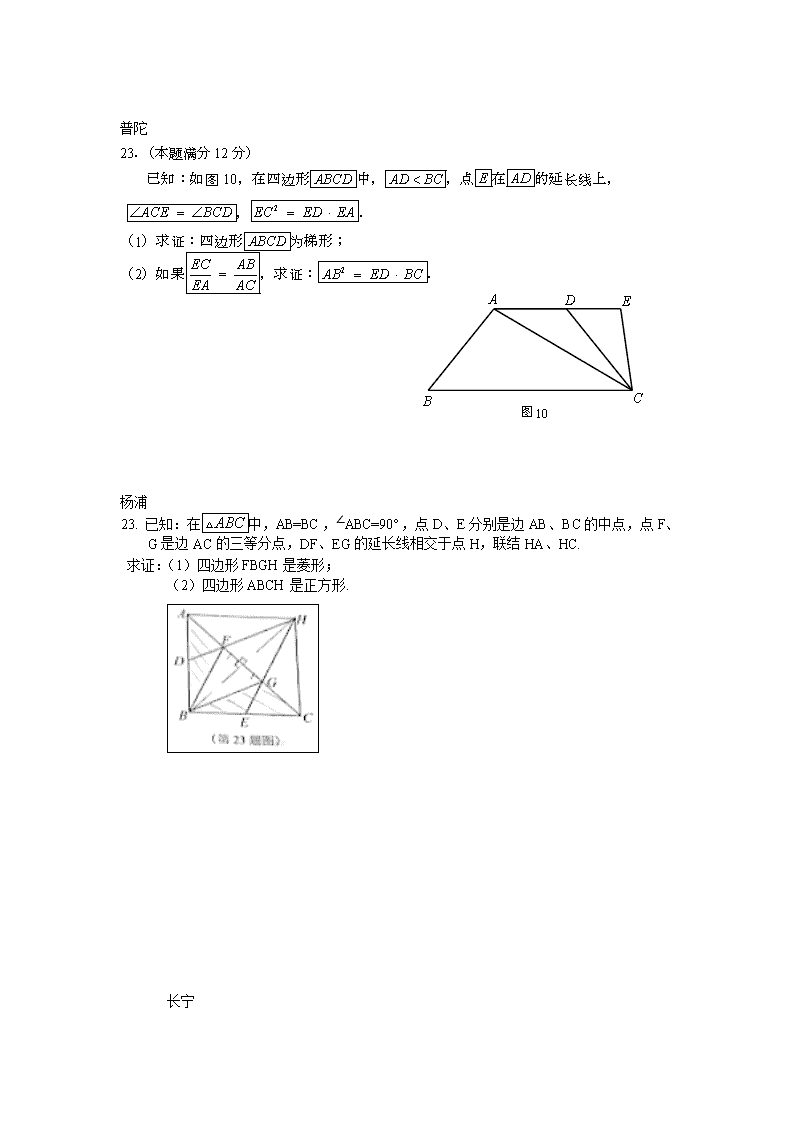
上海市2019年中考二模数学汇编:23题几何证明 闵行 23.(本题共2小题,每小题6分,满分12分) A B C D O E G F (第23题图) 如图,已知四边形ABCD是菱形,对角线AC、BD相交于点O,BD = 2AC.过点A作AE⊥CD,垂足为点E,AE与BD相交于点F.过点C作CG⊥AC,与AE的延长线相交于点G. 求证:(1)△ACG≌△DOA; (2). 宝山 23.(本题满分12分,第(1)、第(2)小题满分各6分) 如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,联结AP并延长AP交CD于F点, (1)求证:四边形AECF为平行四边形; (2)如果PA=PC,联结BP,求证:△APB≅△EPC. 崇明 23.(本题满分12分,每小题满分各6分) 如图7,在直角梯形ABCD中,,,对角线AC、BD相交于点O. A B C D O E F 图7 过点D作,交AC于点F. (1)联结OE,若,求证:; (2)若且,求证:. 奉贤 23.(本题满分12分,每小题满分各6分) A B C D F G E 图8 已知:如图8,正方形ABCD,点E在边AD上,AF⊥BE,垂足为点F,点G在线段BF上,BG=AF. (1)求证:CG⊥BE; (2)如果点E是AD的中点,联结CF,求证:CF=CB. 金山 22. 已知:如图,菱形的对角线与相交于点,若. (1) 求证:是正方形. A B C D O E H F 第23题图 (2) 是上一点,,垂足为,与相交于点,求证:. 普陀 23.(本题满分12分) 已知:如图10,在四边形中,,点在的延长线上, ,. (1)求证:四边形为梯形; 图10 A B C D E (2)如果,求证:. 杨浦 23. 已知:在中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,联结HA、HC. 求证:(1)四边形FBGH是菱形; (2)四边形ABCH是正方形. 长宁 23.(本题满分12分,第(1)小题5分,第(2)小题7分) 图5 A B C D E F O 如图5,平行四边形的对角线交于点,点在边CB的延长线上,且,. (1)求证:四边形是矩形; (2)延长交于点,若,求证:. 黄浦 嘉定 22. 静安 松江 徐汇 答案 闵行 23.证明:(1)在菱形ABCD中,AD = CD,AC⊥BD,OB = OD. ∴ ∠DAC =∠DCA,∠AOD = 90°.……………………………(1分) ∵ AE⊥CD,CG⊥AC, ∴ ∠DCA +∠GCE = 90°,∠G +∠GCE = 90°. ∴ ∠G =∠DCA.…………………………………………………(1分) ∴ ∠G =∠DAC.…………………………………………………(1分) ∵ BD = 2AC,BD = 2OD,∴ AC = OD. ……………………(1分) 在△ACG和△DOA中, ∵ ∠ACG =∠AOD,∠G =∠DAC,AC = OD, ∴ △ACG≌△DOA. ……………………………………………(2分) (2)∵ AE⊥CD,BD⊥AC,∴ ∠DOC =∠DEF = 90°.…………(1分) 又∵ ∠CDO =∠FDE,∴ △CDO∽△FDE.…………………(1分) ∴ .即得 . ……………………(2分) ∵ △ACG≌△DOA,∴ AG = AD = CD. ……………………(1分) 又∵ ,∴ .…………………(1分) 宝山 23.(1)证明:由折叠得到EC垂直平分BP, ………………1分 设EC与BP交于Q,∴BQ=EQ ………………1分 ∵E为AB的中点, ∴AE=EB, ………………1分 ∴EQ为△ABP的中位线,∴AF∥EC, ………………2分 ∵AE∥FC, ∴四边形AECF为平行四边形; ………………1分 (2)∵AF∥EC,∴∠APB=∠EQB=90° ………………1分 由翻折性质∠EPC=∠EBC=90°,∠PEC=∠BEC ………………1分 ∵E为直角△APB斜边AB的中点,且AP=EP, ∴△AEP为等边三角形 , ∠BAP=∠AEP=60°, ………………1+1分 ………………1分 在△ABP和△EPC中, ∠BAP=∠CEP,∠APB=∠EPC,AP=EP ∴△ABP≌△EPC(AAS), ………………1分 崇明 23.(本题满分12分,每小题满分各6分) 证明(1)∵, ∴ ………………………………………………………………(1分) ∴ ………………………………………………………………(2分) ∵ ∴ ……… ………………………………………………………(2分) ∴ …………………………………………………………………(1分) (2)∵,, ∴四边形ABED为平行四边形 又∵ ∴四边形ABED为矩形 ……………………………………………………(1分) ∴, 又∵ ∴ ∴ …………………………………………………………(1分) ∴ ∴…………………………………………………(1分) ∴ ∴…………………………………………………………(1分) ∵ ∴…………………………………………………………(1分) ∴…………………………………………………………………(1分) 奉贤 22. 证明:(1)∵四边形ABCD是正方形,∴.. (1分) ∵AF⊥BE,∴. ∵,∴. (1分) 又∵,∴△△. (2分) ∴. (1分) ∵,∴,即CG⊥BE. (1分) (2)∵,, ∴△∽△.∴. (3分) ∵点E是AD的中点,,∴.∴. (1分) ∵,∴,即. (1分) ∵CG⊥BE,∴. (1分) 金山 23.(1)证明:∵四边形是菱形, ∴,,; (2分) ∴; (1分) ∵; ∴, (1分) ∴; ∴; (1分) ∴四边形是正方形. (1分) (2)证明:∵四边形是正方形; ∴,,,; (1分) ∴,; (1分) ∵,垂足为; ∴,; (1分) 又∵; ∴; (1分) ∴≌; (1分) ∴. (1分) 普陀 23.证明: (1)∵ ,∴. (1分) ∵,∴. (1分) 又∵是公共角,∴△∽△. (1分) ∴. (1分) ∴. ∴∥. (1分) ∵,∴与不平行. ∴四边形是梯形. (1分) (2)∵△∽△. ∴. ∵,∴. (1分) ∴四边形是等腰梯形. (1分) ∴. (1分) ∵∥.∴. ∴. ∵,∴△∽△. (1分) ∴. (1分) ∴. (1分) 杨浦 23.(1)证明略 (2)证明略 长宁 23.(本题满分12分,第(1)小题5分,第(2)小题7分) 证明:(1)∵ ∴ 又 ∵ ∴∽ (2分) ∴ ∵ ∴ (1分) 又 ∵ ∴ (1分) ∵四边形ABCD是平行四边形 ∴四边形ABCD是矩形 (1分) (2)∵ ∽ ∴ 即 , (2分) ∵四边形ABCD是矩形 ∴ 又 ∵, ∴ ∴ 又 ∵ ∴ 又 ∵ ∴∽ (3分) ∴ ∴ (1分) ∵ ∴ (1分) 黄浦 嘉定 静安 松江 徐汇查看更多