高中数学必修2全册同步检测:1-3-2
1-3-2同步检测
一、选择题
1.两球表面积之比为1:4,则它们的半径之比为( )
A.1:2 B.1:4
C.1: D.1:2
2.把半径分别为6cm,8cm,10cm的三个铁球熔成一个大铁球,这个大铁球的半径为( )
A.3cm B.6cm
C.8cm D.12cm
3.球的体积与其表面积的数值相等,则球的半径等于 ( )
A. B.1
C.2 D.3
4.半径为R的球内接一个正方体,则该正方体的体积是( )
A.2R3 B.πR3
C.R3 D.R3
5.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为( )
A.R B.2R
C.3R D.4R
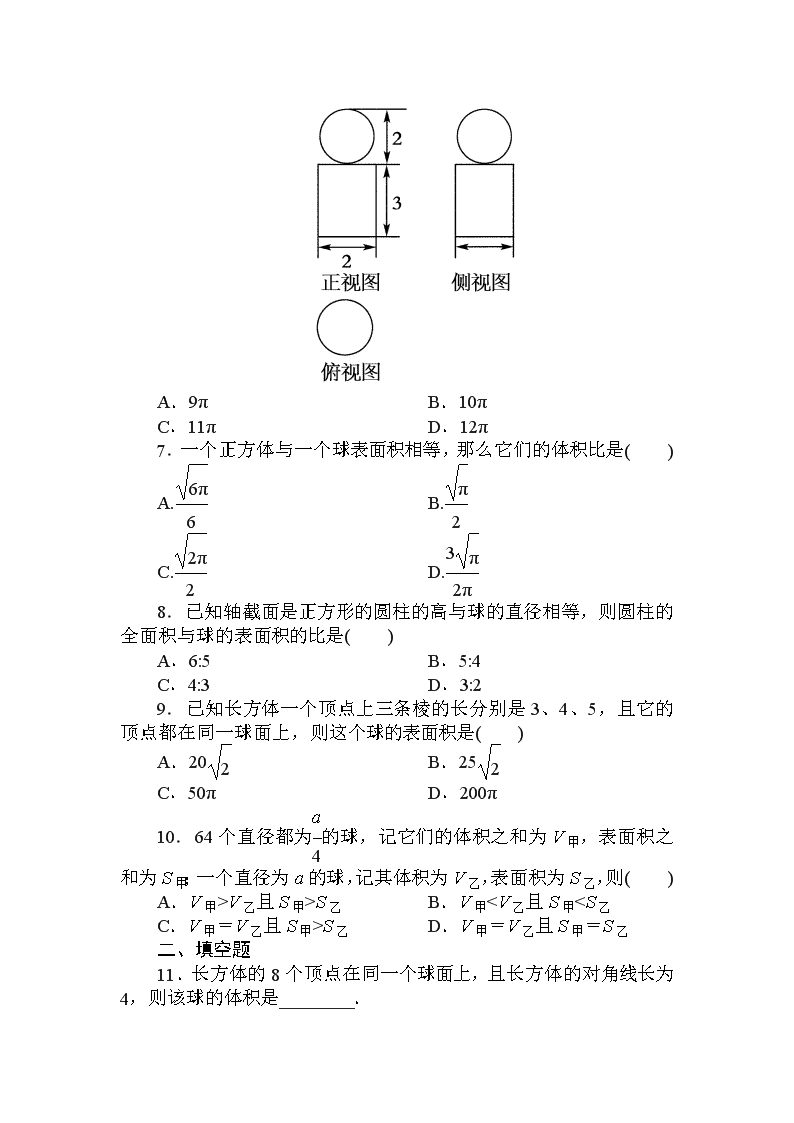
6.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A.9π B.10π
C.11π D.12π
7.一个正方体与一个球表面积相等,那么它们的体积比是( )
A. B.
C. D.
8.已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是( )
A.6:5 B.5:4
C.4:3 D.3:2
9.已知长方体一个顶点上三条棱的长分别是3、4、5,且它的顶点都在同一球面上,则这个球的表面积是( )
A.20 B.25
C.50π D.200π
10.64个直径都为的球,记它们的体积之和为V甲,表面积之和为S甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则( )
A.V甲>V乙且S甲>S乙 B.V甲
S乙 D.V甲=V乙且S甲=S乙
二、填空题
11.长方体的8个顶点在同一个球面上,且长方体的对角线长为4,则该球的体积是________.
12.已知棱长为2的正方体的体积与球O的体积相等,则球O的半径为________.
13.圆柱OO′的底面半径为4,高为,球M的体积等于圆柱OO′的体积,则球M的半径等于________.
14.(2010·湖北高考)圆柱形容器内盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.
三、解答题
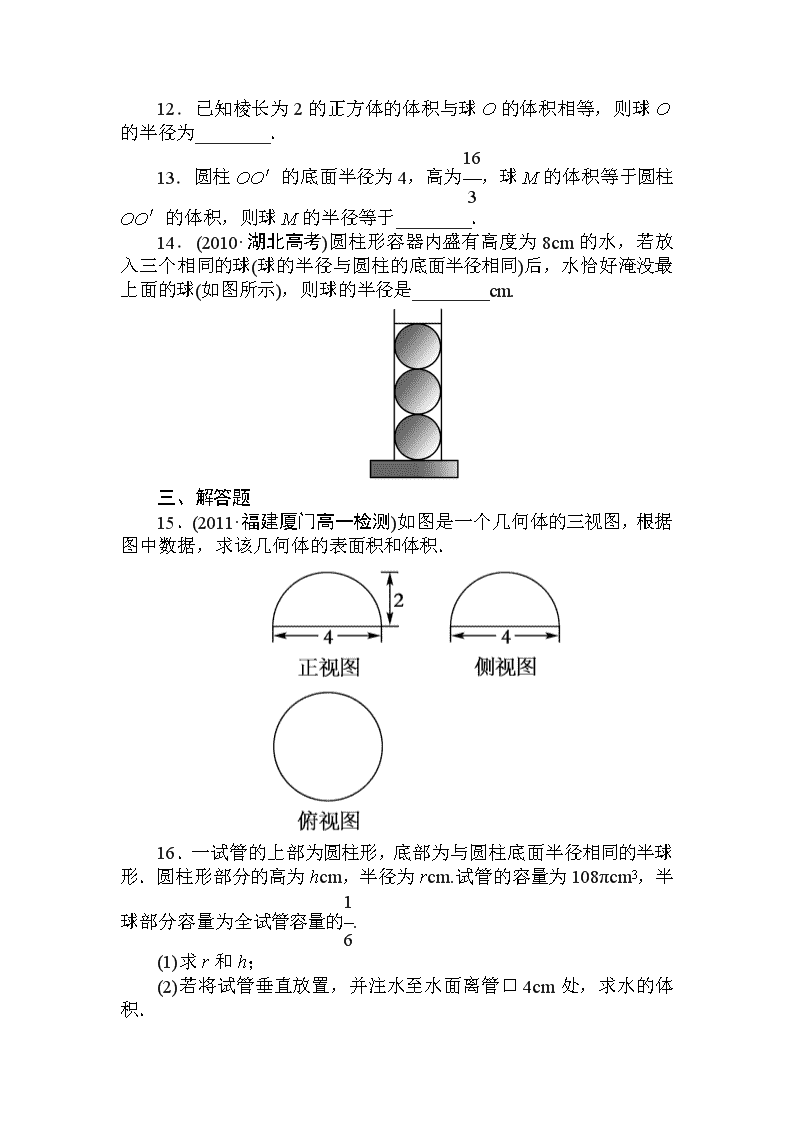
15.(2011·福建厦门高一检测)如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
16.一试管的上部为圆柱形,底部为与圆柱底面半径相同的半球形.圆柱形部分的高为hcm,半径为rcm.试管的容量为108πcm3,半球部分容量为全试管容量的.
(1)求r和h;
(2)若将试管垂直放置,并注水至水面离管口4cm处,求水的体 积.
17.体积相等的正方体、球、(轴截面为正方形)的全面积分别是S1、S2、S3,试比较它们的大小.
18.(2011-2012·杭州高二检测)如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,冰淇淋会从杯子溢出吗?请计算说明理由.
[答案] A
[解析] 由=,得=.
[答案] D
[解析] 方法1:大球半径应大于10cm,故选D
[答案] D
[答案] C
[答案] D
[答案] D
[解析] 本题是三视图还原为几何体的正投影问题,考查识图能力,空间想像能力.由题设可知,该几何体是圆柱的上面有一个球,圆柱的底面半径为1,高为3,球的半径为1,∴该几何体的表面积为
2π×1×3+2π×12+4π×12=12π.
[答案] A
[解析] 由6a2=4πR2得=,∴==3=.
[答案] D
[解析] 设球的半径为R,则圆柱的高h=2R,底面的半径也为R,
∴==.
[答案] C
[解析] 长方体的体对角线即为球的直径,∴2R=,∴R=,S球=4πR2=50π.
[答案] C
[解析] 计算得V甲=πa3,S甲=4πa2,V乙=πa3,S乙=πa2,∴V甲=V乙,且S甲>S乙.
[答案]
[解析] 该球的半径为=2,
则该球的体积是×23=.
[答案]
[解析] 设球O的半径为r,则πr3=23,
解得r=
[答案] 4
[解析] 设球M的半径为r,则πr3=π×42×,解得r=4,即球M的半径为4.
[答案] 4
[解析] 设球的半径为r,则圆柱形容器的高为6r,容积为πr2×6r=6πr3,高度为8cm的水的体积为8πr2,3个球的体积和为3×πr3=4πr3,由题意6πr3-8πr2=4πr3,解得r=4.
[解]由三视图可知此几何体是半径为2的半球.
S=×4πR2+πR2=12π,
V=πR3×=π.
[解析] (1)∵半球部分容量为全试管容量的,
∴半球部分与圆柱体部分容量比为,
即=
∴h=r,πr3×=108π×
∴r=3(cm),h=10(cm).
(2)V=πr3×+πr2×(h-4)
=π×33×+π×32×6=72π(cm3).
[解析] 设正方体的棱长为a,球的半径为R,等边圆柱的底面半径为r,则S1=6a2,S2=4πR2,S3=6πr2.
由题意知,πR3=a3=πr2·2r,
∴R=a,r=a,
∴S2=4π2=4π·a2=a2,
S3=6π2=6π·a2=a2,
∴S23a2=a2,即S1>S3.
∴S1、S2、S3的大小关系是S2
查看更多