八年级下数学课件八年级下册数学课件《角平分线》 北师大版 (3)_北师大版

八年级下数学课件八年级下册数学课件《角平分线》 北师大版 (3)_北师大版

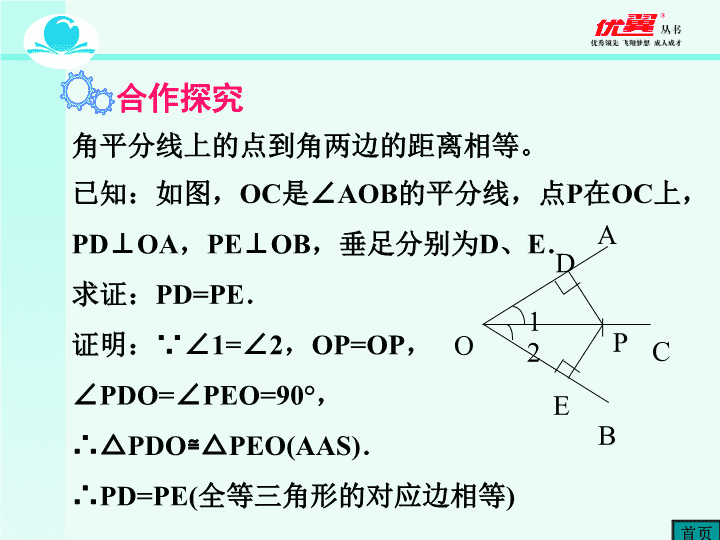
复习 导入 1.4 角平分线 第一章 三角形的证明 第1课时 角平分线 　　还记得角平分线上的点有什么性质吗? 你是怎样得到的? 与小组同学交流。 角平分线上的点到角两边的距离相等。 复习导入 首页 角平分线上的点到角两边的距离相等。 已知：如图，OC是∠AOB的平分线，点P在OC上 ，PD⊥OA，PE⊥OB，垂足分别为D、E． 求证：PD=PE． 证明：∵∠1=∠2，OP=OP， ∠PDO=∠PEO=90°， ∴△PDO≌ △PEO(AAS)． ∴PD=PE(全等三角形的对应边相等) A O C B 1 2 P D E 合作探究 首页 定理：角平分线上的点到这 个角的两边距离相等. ∵OC是∠AOB的平分线,P是 OC上任意,PD⊥OA,PE⊥OB,垂 足分别是D,E(已知) ∴PD=PE(角平分线上的点到这 个角的两边距离相等). A O C B 1 2 P D E 你能写出上面这个定理的逆命题吗? 性质定理:角平分线上的点到这个角的两边距离相等. 如果有一个点到角两边的距离相等，那么这个点 必在这个角的平分线上． 这是一个真命题吗？如果是，请证明；如果不是 请举出反例。 不是真命题，是假命题。在角的外部，也存在到 角两边距离相等的点，但是这个点不在这个角的 平分线上． 　　角平分线性质定理的逆命题：在一个角的内 部且到角的两边距离相等的点，在这个角的角平 分线上。 它是真命题吗? 如果是.请你证明它。 A O C B 1 2 P D E 已知：在∠AOB内部有一点P，且PD⊥OA， PE⊥OB，D、E为垂足且PD=PE，求证：点P在 ∠AOB的角平分线上． 证明：∵PD⊥OA，PE⊥OB， ∴∠PDO=∠ PEO=90° 　　　在Rt△ODP和Rt△OEP中 　　　OP=OP，PD=PE 　　　∴Rt△ODP ≌ Rt△OEP(HL)． 　　　∴∠1=∠2(全等三角形对应角相等)． A O C B 1 2 P D E 判定定理： 在一个角的内部,且到角的两 边距离相等的点,在这个角的平分线上. ∵PD⊥OA,PE⊥OB,垂足分别是 D,E(已知), 且PD=PE, ∴点P在∠AOB的平分线上.(在一 个角的内部,且到角的两边距离相 等的点,在这个角的平分线上). A O C B 1 2 P D E 你能用什么办法平分一个已知角呢？ 1．可以用量角器． 2．使用三角尺，也可以平分一个已知角． 3．用角尺也可以平分一个已知角． 4．用直尺和圆规平分一个已知角． 5. 用折纸的办法也可以平分一个已知角． 已知:∠AOB,如图. 求作:射线OC,使∠AOC=∠BOC. 用尺规作角的平分线. 作法:1.在OA和OB上分别截 取OD,OE,使OD=OE. 2.分别以点D和E为圆心,以 大于DE/2长为半径作弧,两 弧在 ∠AOB内交于点C. 3.作射线OC. 则射线OC就是∠AOB的平分 线. A BO C D E 你能说明射 线OC为什么 是∠AOB的平 分线吗？ 1.利用尺规作出三角形三个内角的平分线。 你发现了什么？ 2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的 两边的距离相等. C ● D ● A B O 温馨提示：本题综合 运用线段的垂直平分 线的性质和角平分线 的性质哦！ 1.角平分线的性质定理： 角平分线上的点到这个角的两边距离相等. 2.角平分线的判定定理： 在一个角的内部,且到角的两边距离相等的点,在 这个角的平分线上. 3.用尺规作角平分线 课堂小结 首页 1.如图,AD,AE分别是△ABC中∠A的内角平分线 外角平分线,它们有什么位置关系? 老师期望:你能说出结论并能证明它. E D AB C F 随堂训练 首页 2.已知:如图,在△ABC中,AD是它的角平分线,且 BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F. 求证:EB=FC. 老师期望:做完题目后,一定要“悟”到点东西,纳 入到自己的认知结构中去. B A E D C F 3.如图,一目标在A区,到期公路,铁路距离相等,离 公路与铁路的交叉处500m.在图上标出它的位置( 比例尺 1:20 000)。 A区