高考文科数学专题复习练习2直线的倾斜角与斜率
122
直线的倾斜角与斜率
1.(2015广西柳州3月模拟,文12,直线的倾斜角与斜率,选择题)过点(2,0)引直线l与曲线y=1-x2交于A,B两点,O为坐标原点,当△AOB的面积取得最大值时,直线l的斜率等于( )
A.33 B.-33 C.±33 D.-3
解析:依题意,曲线y=1-x2是以原点为圆心、1为半径的圆周上位于x轴及其上方的部分(含点(±1,0)).△AOB的面积等于12|OA|·|OB|·sin ∠AOB=12sin ∠AOB的最大值是12,此时∠AOB=90°,圆心(0,0)到直线l的距离等于1×sin 45°=22,结合图形可知,相应直线l的倾斜角为180°-30°=150°,相应直线l的斜率是tan 150°=-33,故选B.
答案:B
126
距离公式
1.(2015宁夏银川二中一模,文5,距离公式,选择题)已知直线x+y-k=0(k>0)与圆x2+y2=4交于不同的两点A,B,O是坐标原点,若|OA+OB|=33|AB|,则实数k=( )
A.1 B.2 C.3 D.2
解析:设AB的中点为D,则OD⊥AB,因为|OA+OB|=33|AB|,故2|OD|=33|AB|,故|AB|=23|OD|.因为|OD|2+14|AB|2=4,故|OD|2=1,即1=|-k|22,因为k>0,k=2,故选B.
答案:B
128
求圆的方程
1.(2015河北石家庄一检,文5,求圆的方程,选择题)若圆C的半径为1,点C与点(2,0)关于点(1,0)对称,则圆C的标准方程为( )
A.x2+y2=1 B.(x-3)2+y2=1
C.(x-1)2+y2=1 D.x2+(y-3)2=1
解析:由题意得点C的坐标为(0,0),所以圆C的标准方程为x2+y2=1,故选A.
答案:A
131
直线与圆的位置关系
8.(2015辽宁大连双基测试,文15,直线与圆的位置关系,填空题)圆x2+y2=1与直线y=kx+2没有公共点的充要条件是 .
解析:依题意,圆x2+y2=1与直线y=kx+2没有公共点的充要条件是圆心到直线的距离大于半径,即2k2+1>1,-3
4,则圆心C(0,0)到直线x0x+y0y=4的距离为|-4|x02+y02<1<2,所以直线x0x+y0y=4与圆x2+y2=4相交,故选C.
答案:C
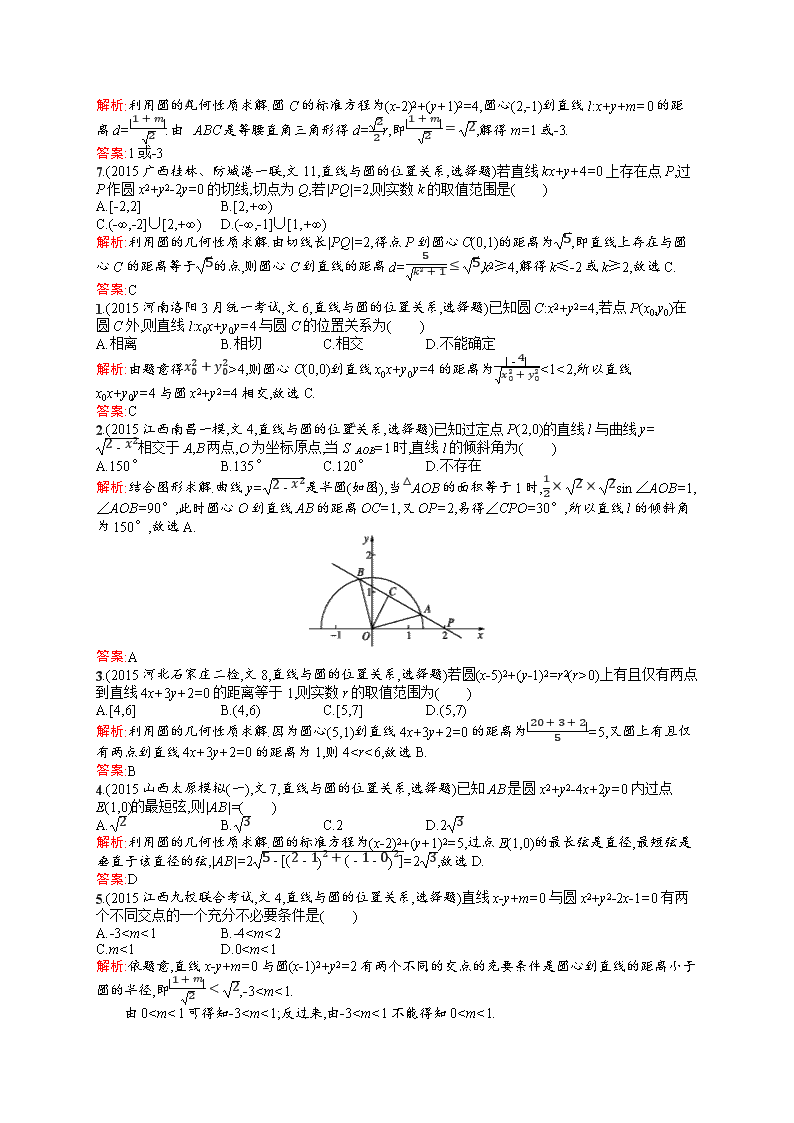
2.(2015江西南昌一模,文4,直线与圆的位置关系,选择题)已知过定点P(2,0)的直线l与曲线y=2-x2相交于A,B两点,O为坐标原点,当S△AOB=1时,直线l的倾斜角为( )
A.150° B.135° C.120° D.不存在
解析:结合图形求解.曲线y=2-x2是半圆(如图),当△AOB的面积等于1时,12×2×2sin ∠AOB=1,∠AOB=90°,此时圆心O到直线AB的距离OC=1,又OP=2,易得∠CPO=30°,所以直线l的倾斜角为150°,故选A.
答案:A
3.(2015河北石家庄二检,文8,直线与圆的位置关系,选择题)若圆(x-5)2+(y-1)2=r2(r>0)上有且仅有两点到直线4x+3y+2=0的距离等于1,则实数r的取值范围为( )
A.[4,6] B.(4,6) C.[5,7] D.(5,7)
解析:利用圆的几何性质求解.因为圆心(5,1)到直线4x+3y+2=0的距离为|20+3+2|5=5,又圆上有且仅有两点到直线4x+3y+2=0的距离为1,则40,n>0)的右焦点与抛物线y2=8x的焦点相同,椭圆的离心率为12,则此椭圆的方程为( )
A.x212+y216=1 B.x216+y212=1
C.x248+y246=1 D.x264+y248=1
解析:依题意得m2-n2=4,2m=12,解得m=4,n2=12,因此所求的椭圆方程为x216+y212=1,故选B.
答案:B
3.(2015河南郑州第二次质量检测,文12,椭圆的几何性质,选择题)已知椭圆x2a2+y2b2=1(a>b>0)的两焦点分别是F1,F2,过点F1的直线交椭圆于P,Q两点,若|PF2|=|F1F2|,且2|PF1|=3|QF1|,则椭圆的离心率为( )
A.35 B.45 C.34 D.325
解析:由题意得|PF1|+|PF2|=2a,|PF1|=2a-2c,|QF1|=23|PF1|=23(2a-2c),QF2=2a-23(2a-2c)=2a3+43c.取PF1的中点M,连接F2M,则F2M⊥PF1,|F2M|2=|F1F2|2-|F1M|2=|F2Q|2-|MQ|2,所以4c2-(a-c)2=2a3+43c2-73a-73c2,化简得5e2-8e+3=0,所以e1=1(舍去),e2=35,即椭圆的离心率为35,故选A.
答案:A
7.(2015河南六市一联,文15,椭圆的几何性质,填空题)过椭圆x225+y216=1的中心任作一直线交椭圆于P,Q两点,F是椭圆的一个焦点,则△PQF面积的最大值是 .
解析:利用等价转化思想求解.设椭圆另一个焦点为F',则四边形F'PFQ是平行四边形,S△PFQ=S△PFF'≤12×2cb=cb=3×4=12,当且仅当点P是短轴的一个端点时取等号,所以△PQF面积的最大值是12.
答案:12
4.(2015山西3月质量监测,文12,椭圆的几何性质,选择题)已知A,B分别为椭圆x2a2+y2b2=1(a>b>0)的右顶点和上顶点,直线y=kx(k>0)与椭圆交于C,D两点,若四边形ACBD的面积的最大值为2c2,则椭圆的离心率为( )
A.13 B.12 C.33 D.22
解析:设C(x0,y0),则D(-x0,-y0).
联立y=kx,x2a2+y2b2=1,消去y整理得(a2k2+b2)x2-a2b2=0,解得x0=aba2k2+b2,则y0=abka2k2+b2,
则S四边形ACBD=2×12ay0+12bx0
=a2bka2k2+b2+ab2a2k2+b2=ab·ak+ba2k2+b2
=aba2k2+2abk+b2a2k2+b2=ab1+2aba2k+b2k
≤ab·1+2ab2a2k·b2k=2ab,
当且仅当a2k=b2k,即k=ba时,等号成立,所以2ab=2c2,即4c4=2a2(a2-c2),2e4+e2-1=0,解得e=22,故选D.
答案:D
10.
(本小题满分12分)(2015宁夏银川一中二模,文20,椭圆的几何性质,解答题)如图,设椭圆y2a2+x2b2=1(a>b>0)的右顶点与上顶点分别为A,B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O,P.
(1)若点P在直线y=32x上,求椭圆的离心率;
(2)在(1)的条件下,设M是椭圆上一动点,且点N(0,1)到椭圆上的点的最近距离为3,求椭圆的方程.
解:(1)由题意知,圆A的方程为(x-b)2+y2=b2,
圆B的方程为x2+(y-a)2=a2,
解方程组(x-b)2+y2=b2,x2+(y-a)2=a2,
得P2a2ba2+b2,2ab2a2+b2.(3分)
因为点P在直线y=32x上,
所以2ab2a2+b2=32·2a2ba2+b2,
即b2=34a2,
所以a2-c2=34a2⇒e=ca=12.(6分)
(2)由(1)有b2=34a2,所以此时所求椭圆方程为y2a2+4x23a2=1.
设M(x,y)是椭圆上一点,
则|MN|2=x2+(y-1)2=34a2-34y2+y2-2y+1
=14(y-4)2-3+34a2,其中-a≤y≤a.(9分)
1°若0b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若椭圆C的中心到直线AB的距离为66|F1F2|,则椭圆C的离心率e=( )
A.22 B.32 C.23 D.33
解析:依题意,设椭圆C的焦距为2c(cb>0)的左、右焦点分别为F1,F2,焦距为2c.直线y=3(x+c)与椭圆的一个交点为M,O为坐标原点,若|OM|=c,则椭圆的离心率是 .
解析:由题意可得△MF1F2是直角三角形,且∠MF1F2=60°,|F1F2|=2c,则|MF1|=c,|MF2|=3c,由椭圆定义可得|MF1|+|MF2|=(1+3)c=2a,所以椭圆的离心率e=ca=21+3=3-1.
答案:3-1
137
直线与椭圆的位置关系
1.
(本小题满分12分)(2015河北衡水中学二模,文20,直线与椭圆的位置关系,解答题)已知圆O:x2+y2=8交x轴于A,B两点,曲线C是以AB为长轴,离心率为22的椭圆.
(1)求椭圆的标准方程;
(2)如图,若直线PQ与椭圆C交于G,H两点,交x轴于点E(-2,0),且EG=3HE,试求此时弦PQ的长.
解:(1)设椭圆的标准方程为x2a2+y2b2=1(a>b>0),
则a=22,ca=22,从而a=22,c=2.
故b=2,∴椭圆的标准方程为x28+y24=1.(5分)
(2)设G(x1,y1),H(x2,y2),
则x12+2y12=8,x22+2y22=8.①
∵EG=3HE,∴(x1+2,y1)=3(-2-x2,-y2),
即x1=-8-3x2,y1=-3y2.
将x1,y1代入①,解得x2=-83,y2=-23(舍去正值),
∴kPQ=1,∴PQ:x-y+2=0,
从而圆心O(0,0)到直线PQ的距离d=22=2,
∴|PQ|=2R2-d2=26.(12分)
2.(本小题满分12分)(2015宁夏银川质量检测,文20,直线与椭圆的位置关系,解答题)已知椭圆C的对称中心为原点O,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点1,32在该椭圆上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,若△AF2B的面积为1227,求以F2为圆心且与直线l相切的圆的方程.
解:(1)椭圆C的方程为x24+y23=1.(4分)
(2)①当直线l⊥x轴时,可得A-1,-32,B-1,32,△AF2B的面积为3,不符合题意.(6分)
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1).
代入椭圆方程得(3+4k2)x2+8k2x+4k2-12=0,
显然Δ>0成立,设A(x1,y1),B(x2,y2),
则x1+x2=-8k23+4k2,x1x2=8k2-123+4k2,
可得|AB|=12(k2+1)3+4k2.(9分)
又圆F2的半径r=2|k|1+k2,
所以△AF2B的面积S=12|AB|r
=12|k|k2+13+4k2=1227,
化简得17k4+k2-18=0,解得k=±1,r=2,
所以所求圆的方程为(x-1)2+y2=2.(12分)
3.(本小题满分12分)(2015东北三省三校二联,文20,直线与椭圆的位置关系,解答题)椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),椭圆C的上顶点与右顶点的距离为3,过F2的直线与椭圆C交于A,B两点.
(1)求椭圆C的方程;
(2)点M在直线x=2上,直线MA,MB的斜率分别为k1,k2,若k1+k2=2,求证:点M为定点.
(1)解:由题意知a2+b2=3,a2-b2=1⇒a2=2,b2=1⇒x22+y2=1.(4分)
(2)证明:若直线AB斜率不存在,则AB:x=1.
不妨设A1,22,B1,-22,M(2,m),
则k1=m-222-1=m-22,k2=m+222-1=m+22,
∵k1+k2=2,
∴2m=2,m=1.(6分)
若直线AB斜率存在,设为k,
则直线AB的方程为y=k(x-1),设A(x1,y1),B(x2,y2),M(2,m).
y=k(x-1),x22+y2=1⇒(1+2k2)x2-4k2x+2(k2-1)=0.
x1+x2=4k21+2k2,x1x2=2(k2-1)1+2k2,(7分)
k1=k(x1-1)-mx1-2,k2=k(x2-1)-mx2-2,
k1+k2=2kx1x2-(3k+m)(x1+x2)+4(k+m)x1x2-2(x1+x2)+4(8分)
=4k2m+4m2(k2+1)=2,
∴m=1,(10分)
∴M为定点(2,1).(12分)
138
双曲线的定义与标准方程
1.(2015吉林省吉林市二调,文4,双曲线的定义与标准方程,选择题)若椭圆x23-y2m=1的一个焦点为F(2,0),则实数m=( )
A.±1 B.-1 C.3 D.±3
解析:由题意知m<0,且3-(-m)=(2)2,得m=-1,故选B.
答案:B
2.(2015辽宁重点中学协作体模拟,文10,双曲线的定义与标准方程,选择题)下列四个命题:
①样本相关系数r满足:|r|≤1,而且|r|越接近于1,线性相关关系越强;
②回归直线就是散点图中经过样本数据点最多的那条直线;
③命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
④已知点A(-1,0),B(1,0),若|PA|-|PB|=2,则动点P的轨迹为双曲线的一支.
其中正确命题的个数为( )
A.1 B.2 C.3 D.4
解析:依题意,对于①,易知是正确的;对于②,易知是错误的;对于③,命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”的逆否命题是“已知x,y∈R,若x=2且y=1,则x+y=3”,且命题“已知x,y∈R,若x=2且y=1,则x+y=3”是真命题,因此命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题,③正确;对于④,|PA|-|PB|=2=|AB|,因此动点P的轨迹是以B为端点的射线y=0(x≥1),④不正确.综上所述,其中正确的命题的个数为2,故选B.
答案:B
3.(2015江西南昌二模,文16,双曲线的定义及标准方程,填空题)过原点的直线l与双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右两支分别相交于A,B两点,F(-3,0)是双曲线C的左焦点,若|FA|+|FB|=4,FA·FB=0,则双曲线C的方程是 .
解析:如图所示,设双曲线的右焦点为F2(3,0),连接F2A,F2B,由双曲线的对称性和FA·FB=0知四边形AFBF2为矩形,由|FA|+|FB|=4得|FA|+|AF2|=4,又因为|FA|-|AF2|=2a,所以|FA|=2+a,|F2A|=2-a,由|F2A|2+|FA|2=(2-a)2+(2+a)2=(23)2,得a2=2,b2=1,所以双曲线的方程为x22-y2=1.
答案:x22-y2=1
139
双曲线的几何性质
1.(2015辽宁东北育才学校五模,文9,双曲线的几何性质,选择题)已知双曲线C:x23-y2=1的左、右焦点分别为F1,F2,过点F2的直线与双曲线C的右支相交于P,Q两点,且点P的横坐标为2,则△PF1Q的周长为( )
A.43 B.1433 C.53 D.1633
解析:依题意,a=3,b=1,故c=2,故F1(-2,0),F2(2,0),由于点P的横坐标为2,可知PQ⊥x轴,将x=2代入x23-y2=1中,解得y=±33,故|PF2|=|QF2|=33,故|PF1|=|QF1|=|PF2|2+|F1F2|2=733,故△PF1Q的周长为733+733+233=1633,故选D.
答案:D
2.(2015黑龙江哈尔滨第六中学二模,文9,双曲线的几何性质,选择题)已知双曲线x22-y2b2=1(b>0)的左、右焦点分别为F1,F2,点P(3,y0)在该双曲线上,若PF1·PF2=0,则双曲线的渐近线方程为( )
A.y=±x B.y=±2x C.y=±3x D.y=±2x
解析:因为P(3,y0),F1(-c,0),F2(c,0),PF1·PF2=0,所以(-c-3,-y0)·(c-3,-y0)=0,即3-c2+y02=0.
又因为32-y02b2=1,所以y02=12b2,得3-(2+b2)+12b2=0,解得b2=2,所以渐近线的方程为y=±x,故选A.
答案:A
3.(2015宁夏银川一中二模,文10,双曲线的几何性质,选择题)以双曲线x24-y2m=1(m>0)的离心率为半径,以右焦点为圆心的圆与该双曲线的渐近线相切,则m的值为( )
A.32 B.13 C.43 D.14
解析:依题意,该双曲线的右焦点到渐近线的距离等于m,于是有m=1+m4,解得m=43,故选C.
答案:C
4.(2015东北三校一联,文15,双曲线的几何性质,填空题)已知双曲线C:y216-x24=1,点P与双曲线C的焦点不重合.若点P关于双曲线C的上、下焦点的对称点分别为点A,B,点Q在双曲线C的上支上,点P关于点Q的对称点为点P1,则|P1A|-|P1B|= .
解析:由题意得QF1为△PAP1的中位线,QF2为△PBP1的中位线,所以|P1A|-|P1B|=2(|QF1|-|QF2|)=2×(-2a)=-16.
答案:-16
5.(2015黑龙江哈尔滨第三中学二模,文15,双曲线的几何性质,填空题)过双曲线x2a2-y2b2=1的右焦点F作一条直线,当直线斜率为2时,直线与双曲线左、右两支各有一个交点;当直线斜率为3时,直线与双曲线右支有两个不同交点,则双曲线离心率的取值范围为 .
解析:利用渐近线的斜率建立基本量的关系.
由题意可得20,b>0)右焦点为F,O为坐标原点,以OF为直径的圆与双曲线C的一条渐近线相交于O,A两点,若△AOF的面积为4,则a的值为( )
A.22 B.3 C.4 D.5
解析:依题意得OA⊥AF,焦点F到渐近线的距离AF=b,S△OAF=12ab=4,又e=1+ba2=52,因此a=2b,2b2=8,b=2,a=4,故选C.
答案:C
7.(2015吉林长春质量监测(二),文12,双曲线的几何性质,选择题)若F(c,0)是双曲线x2a2-y2b2=1(a>b>0)的右焦点,过点F作该双曲线一条渐近线的垂线与两条渐近线交于A,B两点,O为坐标原点,△OAB的面积为12a27,则该双曲线的离心率e=( )
A.53 B.43 C.54 D.85
解析:由题可知,过第一、三象限的渐近线的倾斜角为θ,则tan θ=ba,tan 2θ=2aba2-b2,因此△OAB的面积可以表示为12·a·atan 2θ=a3ba2-b2=12a27,解得ba=34,则e=54,故选C.
答案:C
10.(2015广西柳州3月模拟,文15,双曲线的几何性质,填空题)已知点P是双曲线x2a2-y2=1(a>0)上的动点,F1,F2分别是其左、右焦点,若|PF1|=|PF2|+2,则此双曲线的渐近线方程是 .
解析:依题意得|PF1|-|PF2|=2=2a,a=1,因此该双曲线的渐近线方程是y=±x.
答案:y=±x
8.(2015吉林省吉林市二调,文11,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1的焦点到其渐近线的距离等于2,抛物线y2=2px的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为( )
A.y2=4x B.y2=42x C.y2=82x D.y2=8x
解析:由题意知(c,0)到直线bx-ay=0的距离为bca2+b2=bcc=b=2,在x2a2-y2b2=1中,令x=-c,得c2a2-y2b2=1,即y=b2a,由题意知2×4a=4,得a=2,c=22,又因为p2=c,所以p=42,y2=82x,故选C.
答案:C
9.(2015贵州适应性考试,文10,双曲线的几何性质,选择题)已知圆C的圆心在y轴的负半轴上,且与x轴相切,被双曲线x24-y212=1的一条渐近线截得的弦长为3,则圆C的方程为( )
A.x2+(y+1)2=1 B.x2+(y+3)2=3
C.x2+y+322=34 D.x2+(y+2)2=4
解析:设圆心C(0,b),b<0,则半径r=|b|,双曲线的一条渐近线方程为3x-y=0,则该直线被圆C截得的弦长3=2b2-|b|22,整理得b2=1,则b=-1,故圆C的方程为x2+(y+1)2=1,故选A.
答案:A
11.(2015山西四校三联,文4,双曲线的几何性质,选择题)若椭圆x2a2+y2b2=1(a>b>0)的离心率为12,则双曲线x2a2-y2b2=1的渐近线方程为( )
A.y=±32x B.y=±3x
C.y=±12x D.y=±x
解析:依题意得1-ba2=12,ba=32,因此双曲线x2a2-y2b2=1的渐近线方程为y=±bax=±32x,故选A.
答案:A
12.(2015江西三校联考,文10,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1,过其左焦点F作圆x2+y2=a2的两条切线,切点记作C,D,原点为O,∠COD=2π3,其双曲线的离心率为( )
A.32 B.2 C.3 D.233
解析:连接OC,则有OC⊥FC,∠FOC=π3,cos ∠FOC=ac=12,于是有e=ca=2,即该双曲线的离心率是2,故选B.
答案:B
13.(2015河南十校测试(四),文10,双曲线的几何性质,选择题)以原点O为中心,焦点在x轴上的双曲线C,有一条渐近线的倾斜角为60°,点F是该双曲线的右焦点,位于第一象限内的点M在双曲线C上,且点N是线段MF的中点.若|ON|=|NF|+1,则双曲线C的方程为( )
A.x2-y23=1 B.x2-y29=1
C.x24-y212=1 D.3x2-y2=1
解析:结合已知条件的几何特征与双曲线的概念灵活地求解.设双曲线的左焦点为T,连接TM,O,N分别是TF,MF的中点,则ON是△TMF的中位线,因为|ON|=|NF|+1,所以|TM|=|MF|+2,即|TM|-|MF|=2.结合双曲线的概念可知a=1,又ba=tan π3=3,b=3,所以双曲线的方程为x2-y23=1,故选A.
答案:A
15.(2015江西九校联合考试,文16,双曲线的几何性质,填空题)若双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,过F2的直线与双曲线的右支相交于A,B两点,若△F1AB是以点A为直角顶点的等腰直角三角形,则e2= .
解析:依题意,设|AF1|=|AB|=m,则|BF1|=2m,|AF2|=m-2a,|BF2|=2m-2a.
又|AF2|+|BF2|=|AB|,因此(m-2a)+(2m-2a)=m,4a2=m22.
在Rt△AF1F2中,4c2=|F1F2|2=|AF1|2+|AF2|2=5-222m2.
因此e2=4c24a2=5-22.
答案:5-22
14.(2015江西八校联考,文10,双曲线的几何性质,选择题)已知F1,F2分别是双曲线x2a2-y2b2=1的左、右焦点,P为双曲线右支上的任意一点且|PF1|2|PF2|=8a,则双曲线离心率的取值范围是( )
A.(1,2] B.[2,+∞) C.(1,3] D.[3,+∞)
解析:利用双曲线定义和几何性质求解.由题意可得|PF1|-|PF2|=|PF1|-|PF1|28a=2a,解得|PF1|=4a≥a+c,3a≥c,所以离心率10,b>0)的右焦点为F,过点F的直线l交双曲线的渐近线于A,B两点,且与其中的一条渐近线垂直,若AF=4FB,则该双曲线的离心率是( )
A.5 B.25 C.2105 D.105
解析:设双曲线的两条渐近线方程分别为l1:y=bax,l2:y=-bax,直线l⊥l1,过点F的直线l:y=-ab(x-c),联立l,l1,解得yB=abc,联立l,l2,解得yA=abcb2-a2.
又AF=4FB,则|AF||BF|=|yA||yB|=4,且b0,b>0)的左、右焦点分别为F1,F2,P为双曲线上任一点,且PF1·PF2的最小值的取值范围是-34c2,-12c2,则该双曲线的离心率的取值范围为( )
A.(1,2) B.[2,2] C.(1,2] D.[2,+∞)
解析:设P(m,n),则m2a2-n2b2=1,即m2=a21+n2b2.
又F1(-c,0),F2(c,0),所以PF1=(-c-m,-n),PF2=(c-m,-n),所以PF1·PF2=(-c-m,-n)(c-m,-n)=m2+n2-c2=a21+n2b2+n2-c2=n21+a2b2+a2-c2≥a2-c2,当且仅当n=0时取等号.
由题意得-34c2≤a2-c2≤-12c2,即-34e2≤1-e2≤-12e2,解得2≤e2≤4,所以2≤e≤2,故选B.
答案:B
19.(2015山西大附中第五次月考,文9,双曲线的几何性质,选择题)过双曲线x2a2-y2b2=1(b>a>0)的左焦点F(-c,0)(c>0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,O为坐标原点,若OE=12(OF+OP),则双曲线的离心率为( )
A.1+52 B.3+32 C.52 D.1+32
解析:设双曲线的右焦点为F'(c,0),则F'为抛物线y2=4cx的焦点,O为FF'的中点,由OE=12(OF+OP)得E为FP的中点,连接F'P,则OE∥PF',OE=a,PF'=2a,PF'⊥PF,FF'=2c,由EF=c2-a2=b得PF=2b,设P(x,y),则由抛物线的定义得x+c=2a,x=2a-c,过点F作x轴的垂线,点P到该垂线的距离为2a,由勾股定理得y2+4a2=4b2,所以4c(2a-c)+4a2=4(c2-a2),即e2-e-1=0,解得e=5+12,故选A.
答案:A
21.(2015河北唐山一模,文11,双曲线的几何性质,选择题)F是双曲线C:x2a2-y2b2=1(a>0,b>0)的右焦点,过点F向C的一条渐近线引垂线,垂足为A,交另一条渐近线于点B.若2FA=FB,则C的离心率是( )
A.233 B.143 C.2 D.2
解析:由题意得OA⊥BA且2AF=BF,过点F作OB的垂线,垂足为点E,则EF=AF,在Rt△BEF中,BF=2EF,所以∠EBF=30°,则∠AOB=60°,∠BOF=12∠AOB=30°,所以ba=tan 30°=33,则c2-a2a2=13,e2=43,e=233,故选A.
答案:A
23.(2015河北保定一模,文13,双曲线的几何性质,填空题)双曲线2x2-y2=1的离心率为 .
解析:由题设知a2=12,b2=1,所以e=1+ba2=1+2=3.
答案:3
22.(2015山西太原模拟(一),文11,双曲线的几何性质,选择题)已知点F1,F2是双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,若双曲线左支上存在点P与点F2关于直线y=bax对称,则该双曲线的离心率为( )
A.2 B.52 C.2 D.5
解析:利用双曲线的定义、几何性质求解.
由题意可得线段PF2被渐近线y=bax垂直平分,记交点为A,则AF2=b,|PF2|=2b,由双曲线定义和三角形中位线得|OA|=12|PF1|=12(2b-2a)=b-a,在直角三角形OAF2中,由勾股定理得(b-a)2+b2=c2,化简得b=2a,b2=c2-a2=4a2,c=5a,所以离心率e=ca=5,故选D.
答案:D
28.(2015河南洛阳3月统一考试,文13,双曲线的几何性质,填空题)双曲线y24-x2b=1(b>0)的离心率为2,则此双曲线的焦点到渐近线的距离为 .
解析:由题意得双曲线的离心率e=ca=4+b24=2,解得b=2,则c=22,双曲线的渐近线方程为y=±bax=±x,则焦点(±22,0)到渐近线的距离为|±22|12+(±1)2=2.
答案:2
24.(2015江西南昌一模,文8,双曲线的几何性质,选择题)若双曲线C:x2a2-y2b2=1的一条渐近线倾斜角为π6,则双曲线C的离心率为( )
A.2或3 B.233 C.2或233 D.2
解析:建立基本量的关系求解.由题意可得双曲线的一条渐近线方程为y=33x,且双曲线的焦点在x轴上,所以ba=33,离心率e=ca=a2+b2a2=1+ba2=1+13=233,故选B.
答案:B
25.(2015江西赣州摸底考试,文4,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1(b>a>0)的两条渐近线的夹角为60°,则双曲线的离心率为( )
A.3 B.2 C.43 D.233
解析:由条件得双曲线的两条渐近线方程为y=±bax,因为b>a>0,所以双曲线的两条渐近线的倾斜角分别为60°和120°,则ba=3,所以e=1+ba2=2,故选B.
答案:B
26.(2015河北石家庄一检,文11,双曲线的几何性质,选择题)双曲线C:x2a2-y2b2=1(a>0,b>0)的虚轴端点到直线y=a2x的距离为1,则双曲线的离心率的最小值为( )
A.3 B.3 C.2 D.2
解析:由题意得双曲线的一个虚轴端点为(0,b),则有ba4+1=1,即b2=a4+1,则双曲线的离心率e=ca=a2+a4+1a2=1+a2+1a2≥3,当且仅当a=1时,等号成立,故选B.
答案:B
27.(2015河北石家庄二检,文9,双曲线的几何性质,选择题)已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,在双曲线C上存在点P,满足△PF1F2的周长等于双曲线C的实轴长的3倍,则双曲线C的离心率的取值范围是( )
A.1,32 B.0,32 C.1,52 D.0,52
解析:利用双曲线定义和几何性质建立基本量的关系.不妨设点P在双曲线的右支上,则PF1-PF2=2a,又PF1+PF2+2c=6a,两式相加得PF1=4a-c>a+c⇒3a>2c,所以离心率10,b>0)的左、右焦点,过F1的直线l与双曲线的左、右两支分别交于点A,B,若|AB|=|AF2|,∠F1AF2=90°,则双曲线的离心率为( )
A.6+32 B.6+3 C.5+222 D.5+22
解析:设|AF1|=x,|AF2|=y,则有y-x=2a ①,又因为∠F1AF2=90°,所以x2+y2=4c2 ②,F2A⊥BF1,又因为|AB|=|AF2|=y,所以BF2=2y,则|BF1|-|BF2|=x+y-2y=2a ③,联立①②③得e2=c2a2=33-22,所以e=6+3,故选B.
答案:B
30.(2015广西南宁第二次适应性测试,文5,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1的一条渐近线与直线4x-3y+1=0垂直,则双曲线的两条渐近线方程为( )
A.y=±34x B.y=±43x
C.y=±35x D.y=±54x
解析:直线4x-3y+1=0的斜率为43,双曲线的一条渐近线的斜率为-34,即ba=34,因此双曲线的两条渐近线方程为y=±bax=±34x,故选A.
答案:A
31.(2015贵州贵阳高三适应性检测考试(二),文10,双曲线的几何性质,选择题)以双曲线C:x2-y23=1的一个焦点F为圆心的圆与它的渐近线相切,则该圆的面积为( )
A.π B.3π C.6π D.9π
解析:由题意知双曲线C的一条渐近线为3x-y=0,焦点F(2,0),焦点F到渐近线的距离为233+1=232=3=r,所以圆的面积为πr2=3π,故选B.
答案:B
32.(2015宁夏银川质量检测,文6,双曲线的几何性质,选择题)已知中心在原点,焦点在坐标轴上的双曲线的一条渐近线方程为3x-y=0,则该双曲线的离心率为( )
A.233 B.3 C.2或233 D.233或3
解析:利用渐近线建立基本量的关系求解.当双曲线的焦点在x轴上时,ba=3,离心率e=ca=1+ba2=2;当双曲线的焦点在y轴上时,ba=33,离心率e=ca=1+ba2=233,故选C.
答案:C
33.(2015东北三省三校二联,文8,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,以F1F2为直径的圆被直线xa+yb=1截得的弦长为6a,则双曲线的离心率为( )
A.3 B.2 C.3 D.2
解析:依题意,原点到直线xa+yb=1的距离等于aba2+b2,于是有aba2+b22+6a22=c2.
即a2(c2-a2)c2+6a22=c2,2c4-5a2c2+2a4=0,2e4-5e2+2=0,(e2-2)(2e2-1)=0(e>1),解得e=2,双曲线的离心率是2,故选D.
答案:D
34.(2015河南郑州第三次质量检测,文3,双曲线的几何性质,选择题)已知实数4,m,9构成一个等比数列,则圆锥曲线x2m+y2=1的离心率为( )
A.306 B.7 C.306或7 D.56或7
解析:由题意知m2=36,m=±6,当m=6时,该圆锥曲线表示椭圆,此时a=6,b=1,c=5,e=306;当m=-6时,该圆锥曲线表示双曲线,此时a=1,b=6,c=7,e=7,故选C.
答案:C
35.(2015河南郑州第三次质量检测,文12,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1,a,b∈R,F1,F2分别为双曲线的左、右焦点,O为坐标原点,点P为双曲线上一点满足|OP|=3a,且|PF1|,|F1F2|,|PF2|成等比数列,则此双曲线的离心率为( )
A.213 B.73 C.273 D.733
解析:设P(x0,y0)(x0≥a),则x02+y02=9a2,x02a2-y02b2=1,二者联立得x02=9a4+a2b2c2,又因为|PF1|=(x0+c)2+y02=(x0+c)2+b2x02a2-1=cax0+a,同理可得|PF2|=cax0-a,由题意知|PF1|·|PF2|=4c2,所以c2a2x02-a2=4c2,即c2a2×9a4+a2b2c2-a2=4c2,整理得7a2=3c2,所以ca=213.
答案:A
36.(2015河南高考适应性测试,文12,双曲线的几何性质,选择题)已知椭圆C1:x217+y2=1,双曲线C2:x2a2-y2b2=1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则双曲线C2的离心率为( )
A.4 B.41313 C.2 D.1+52
解析:由题意得以曲线C1的长轴为直径的圆的方程为x2+y2=17,双曲线的一条渐近线的方程为y=bax,设A(xA,yA),xA>0,曲线C1与双曲线的渐近线的交点为D(xD,yD),xD>0.
联立y=bax,x2+y2=17得xA=17a2a2+b2,
联立y=bax,x217+y2=1得xD=17a2a2+17b2,由题意得xA=3xD,即17a2a2+b2=3×17a2a2+17b2,解得a2=b2,所以双曲线的离心率为ca=a2+b2a2=2,故选C.
答案:C
37.(2015河南适应性模拟练习,文6,双曲线的几何性质,选择题)已知双曲线x2a2-y2b2=1(a>0,b>0)的一条渐近线方程为y=kx(k>0),离心率e=5k,则双曲线方程为( )
A.x2a2-y24a2=1 B.x2a2-y25a2=1
C.x24b2-y2b2=1 D.x25b2-y2b2=1
解析:由题意知k=ba,所以5ba=ca,c=5b,a=2b,双曲线方程为x24b2-y2b2=1,故选C.
答案:C
140
抛物线的定义与标准方程
1.(2015黑龙江哈尔滨第三中学二模,文11,抛物线的定义与标准方程,选择题)已知点M是抛物线y2=4x上的一点,F为抛物线的焦点,A在圆C:(x-4)2+(y-1)2=1上,则|MA|+|MF|的最小值为( )
A.3 B.4 C.5 D.6
解析:利用抛物线定义和圆的几何性质求解.
过点M作抛物线准线x=-1的垂线,垂足是点N,则由抛物线定义可得|MF|=|MN|,(|MA|+|MF|)min=(|MC|+|MN|)min-r≥5-1=4,当且仅当点C,M,N三点共线时,等号成立,故选B.
答案:B
2.(2015河南高考适应性测试,文4,抛物线的定义与标准方程,选择题)抛物线y=-4x2的准线方程为( )
A.x=1 B.y=1
C.x=116 D.y=116
解析:由题意得抛物线的标准方程为x2=-14y,则其准线方程为y=116,故选D.
答案:D
3.(2015河南六市一联,文11,抛物线的定义与标准方程,选择题)已知点A(0,2),抛物线C1:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,若|FM|∶|MN|=1∶5,则a的值等于( )
A.14 B.12 C.1 D.4
解析:利用抛物线定义,结合图形求解.过点M作抛物线准线的垂线,垂足为点P,则|FM|∶|MN|=|MP|∶|MN|=15=cos∠NMP,sin∠NMP=25,tan∠NMP=2,直线FA的斜率kFA=2-00-a4=-8a=tan(π-∠NMP)=-tan∠NMP=-2,解得a=4,故选D.
答案:D
4.(2015河北石家庄一检,文2,抛物线的定义与标准方程,选择题)抛物线y2=12x的焦点为( )
A.(6,0) B.(0,6)
C.(3,0) D.(0,3)
解析:由抛物线的方程得2p=12,p2=3,所以焦点的坐标为(3,0),故选C.
答案:C
5.(2015河南十校测试(四),文5,抛物线的定义与标准方程,选择题)过点M(1,a)向抛物线C:y2=ax的准线作垂线,垂足为D,若|MD|=|MO|(其中O是坐标原点),则a=( )
A.8 B.4 C.6 D.-8或8
解析:根据抛物线的概念,结合已知信息的几何特征求解.
设抛物线的焦点为Fa4,0(a>0),M(1,a)在x轴上的射影为T,则|MD|=|MF|,
因为|MD|=|MO|,所以|MO|=|MF|.
又MT⊥OF,则T是OF的中点,a8=1,a=8,
故选A.
答案:A
6.(2015江西八校联考,文4,抛物线的定义与标准方程,选择题)已知抛物线y=ax2(a>0)的焦点到准线的距离为2,则a=( )
A.4 B.2 C.14 D.12
解析:抛物线y=ax2(a>0)的标准方程为x2=1ay(a>0),其焦点到准线的距离为2,则12a=2,a=14,故选C.
答案:C
7.(2015河北唐山一模,文3,抛物线的定义与标准方程,选择题)已知抛物线的焦点F(a,0)(a<0),则抛物线的标准方程是( )
A.y2=4ax B.y2=2ax
C.y2=-4ax D.y2=-2ax
解析:先通过抛物线的焦点位置,确定抛物线标准方程的形式,然后再求未知参数p的值.因为抛物线的焦点为F(a,0)(a<0),所以可设其标准方程为y2=-2px(p>0),则p=-2a,所以抛物线的标准方程为y2=4ax,故选A.
答案:A
141
抛物线的几何性质
1.(2015广西桂林、防城港一联,文8,抛物线的几何性质,选择题)已知抛物线y2=4x的焦点为F,准线为l,点P为抛物线上一点,且在第一象限,PA⊥l,垂足为A,若|PF|=4,则直线AF的倾斜角为( )
A.π6 B.π3 C.2π3 D.5π6
解析:由|PF|=4,得xP=3,又P在第一象限,则P(3,23),A(-1,23),又F(1,0),所以直线AF的斜率为-3,倾斜角为2π3,故选C.
答案:C
2.(2015辽宁重点中学协作体模拟,文11,抛物线的几何性质,选择题)已知椭圆x2a2+y2b2=1(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线y2=158(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率是( )
A.815 B.415 C.12 D.23
解析:由四边形ABFC是菱形得知题中的抛物线与椭圆的交点B,C应位于线段AF的垂直平分线x=a-c2上.
由x2a2+y2b2=1,y2=158(a+c)x,得x2a2+15(a+c)8b2x=1,
于是有a-c22a2+158(a-c)×a-c2=1,
即(a-c)2(2a)2=116,a-c2a=14,1-e=12,即有e=12,
该椭圆的离心率是12,故选C.
答案:C
3.(2015贵州八校二联,文11,抛物线的几何性质,选择题)双曲线x24a2-y2b2=1的右焦点F与抛物线y2=4px(p>0)的焦点重合,且在第一象限的交点为M,MF垂直于x轴,则双曲线的离心率是( )
A.22+2 B.22
C.2+1 D.2+2
解析:由题设知F(p,0),又MF⊥x轴,所以M(p,2p).
将M(p,2p)代入双曲线,得p24a2-4p2b2=1,①
又由双曲线的性质知p=4a2+b2,②
结合①②,得b2=4ap,所以e=p2a=b28a2,
而e=1+b2a2=1+2e,
解得e=2+1,故选C.
答案:C
4.(2015宁夏银川一中二模,文14,抛物线的几何性质,填空题)已知抛物线C:y2=2px(p>0)的准线为l,过点M(1,0)且斜率为3的直线与l相交于点A,与C的一个交点为B,若AM=MB,则p等于 .
解析:依题意得点A-p2,-3p2+1关于点M(1,0)的对称点B2+p2,3p2+1位于抛物线y2=2px上,于是有3p2+12=2p2+p2,解得p=2.
答案:2
5.(2015贵州贵阳监测考试(一),文11,抛物线的几何性质,选择题)已知抛物线C1:y=12px2(p>0)的焦点与双曲线C2:x23-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
A.316 B.38 C.233 D.433
解析:利用导数、三点共线等知识求解.抛物线C1的焦点F0,p2,双曲线C2的右焦点F'(2,0).
由y'=1px=13,解得xM=13p,
则yM=16p,则F0,p2,F'(2,0),M13p,16p三点共线,所以p2-2=p2-p6-13p,解得p=43=433,故选D.
答案:D
6.(2015甘肃第二次诊断考试,文11,抛物线的几何性质,选择题)双曲线C1:x2a2-y2b2=1(a>0,b>0)与抛物线C2:y2=2px(p>0)相交于A,B两点,公共弦AB恰过它们的公共焦点F,则双曲线的一条渐近线的倾斜角所在区间可能是( )
A.π3,π2 B.π4,π3
C.π6,π4 D.0,π6
解析:由双曲线和抛物线的焦点重合可得p24=a2+b2,且点p2,±p在双曲线上,所以p24a2-p2b2=1.(*)
将p2=4(a2+b2)代入(*)得b2a2-4a2b2=4.
令b2a2=k2,则k2-4k2=4,解得k2=2+22>3,
所以渐近线y=bax的倾斜角所在区间可能是π3,π2,故选A.
答案:A
9.(2015东北三省四市一联,文9,抛物线的几何性质,选择题)已知抛物线y2=2px(p>0)与椭圆x2a2+y2b2=1(a>b>0)有相同的焦点F,点A是两曲线的一个公共点,且AF⊥x轴,则椭圆的离心率为( )
A.3-1 B.2-1
C.5-12 D.22-12
解析:依题意,设椭圆的左焦点为F'.
因为右焦点Fp2,0,故F'-p2,0.
因为A是两曲线的公共点,且AF⊥x轴,不妨设点A在第一象限,故Ap2,p.
由椭圆定义可知2a=|AF|+|AF'|=p2-p22+(0-p)2+-p2-p22+(0-p)2=(2+1)p.
又2c=|FF'|=p,故椭圆的离心率e=2c2a=p(2+1)p=2-1,故选B.
答案:B
10.(2015河北石家庄一模,文10,抛物线的几何性质,选择题)已知抛物线y2=2px(p>0)的焦点F恰好是双曲线x2a2-y2b2=1(a>0,b>0)的一个焦点,两条曲线的交点的连线过点F,则双曲线的离心率为( )
A.2 B.3
C.1+3 D.1+2
解析:因为抛物线的焦点F恰好是双曲线的焦点,所以p2=c,根据两条曲线的对称性可知,两条曲线的公共弦是它们公共的通径,而抛物线的通径长度为2p,双曲线的通径长度为2b2a,则2b2a=4c,即c2-a2=2ac,所以e2-2e-1=0(e>1),e=1+2,故选D.
答案:D
11.(2015甘肃兰州实战,文6,抛物线的几何性质,选择题)已知点F是抛物线y2=4x的焦点,M,N是该抛物线上两点,|MF|+|NF|=6,则MN中点到准线距离为( )
A.32 B.2 C.3 D.4
解析:设点M,N的横坐标分别为x1,x2,则有(x1+1)+(x2+1)=6,x1+x2=4,x1+x22=2,即线段MN的中点的横坐标是2,线段MN的中点到准线x=-1的距离为3,故选C.
答案:C
12.(2015河南郑州第二次质量检测,文6,抛物线的几何性质,选择题)已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其一条渐近线的倾斜角为30°,则该双曲线的标准方程为( )
A.x29-y227=1 B.y29-x227=1
C.y212-x224=1 D.y224-x212=1
解析:设双曲线的方程为y2a2-x2b2=1(a>0,b>0),
则有a2+b2=36,ab=tan30°,解得a=3,b=33.
因此双曲线的方程为y29-x227=1,故选B.
答案:B
13.(2015宁夏银川质量检测,文14,抛物线的几何性质,填空题)若M是抛物线y2=4x上一点,且在x轴上方,F是抛物线的焦点,直线FM的倾斜角为60°,则|FM|= .
解析:利用抛物线定义求解.
由题意可得直线FM的方程为y=3(x-1),代入抛物线y2=4x中,化简得3x2-10x+3=0,解得x=13或3.
又点M在x轴上方,则xM=3,
所以|FM|=xM+p2=3+1=4.
答案:4
14.(2015河北衡水中学二模,文11,抛物线的几何性质,选择题)已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA·OB=2(其中O为坐标原点),则△AFO与△BFO面积之和的最小值是( )
A.28 B.24 C.22 D.2
解析:由题意,设A(a2,a),B(b2,b)(ab<0),
∴OA·OB=a2b2+ab=2⇒ab=-2.
又∵F是抛物线y2=x的焦点,∴F14,0.
∴S△AFO+S△BFO=12×14×|b-a|.
∵|b-a|2=a2+b2-2ab≥-2ab-2ab=-4ab=8,
当且仅当a=-b时,等号成立,
∴|b-a|min=22,S△AFO+S△BFO的最小值为24,故选B.
答案:B
15.(2015山西四校三联,文12,抛物线的几何性质,选择题)已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则双曲线的离心率为( )
A.5-12 B.2+12
C.2+1 D.5-1
解析:依题意,设点P(x,y),其中y≥0,则点A(0,-1),|PB|=y+1,|PA|=x2+(y+1)2=4y+(y+1)2,
当y=0时,m=|PA||PB|=1;
当y>0时,10,b>0)的右焦点是抛物线y2=8x的焦点,两曲线的一个公共点为P,且|PF|=5,则该双曲线的离心率为( )
A.52 B.5 C.2 D.233
解析:利用抛物线定义求出点P的坐标,代入双曲线方程求解.
由题意可得双曲线的半焦距c=2,由抛物线定义可得xP=3,代入抛物线方程得P(3,±26),将点P代入双曲线方程得9a2-24b2=1,又a2+b2=c2=4,解得a=1.
所以该双曲线的离心率e=ca=2,故选C.
答案:C
19.(2015江西赣州摸底考试,文7,抛物线的几何性质,选择题)已知抛物线C:y2=8x焦点为F,点P是C上一点,若△POF的面积为2,则|PF|=( )
A.52 B.3 C.72 D.4
解析:由题设得焦点为F(2,0),抛物线准线方程为x=-2,设P(x,y),则有S△POF=12|OF||y|=12·2|y|=2,解得y=±2.
由y2=8x得x=12,所以|PF|=12+2=52,故选A.
答案:A
20.(2015山西3月质量监测,文10,抛物线的几何性质,选择题)已知F为抛物线C:y2=4x的焦点,点E在C的准线上,且在x轴上方,线段EF的垂直平分线与C的准线交于点Q-1,32,与C交于点P,则△PEF的面积为( )
A.5 B.10 C.15 D.20
解析:由题意得抛物线的焦点坐标为F(1,0),准线方程为x=-1,则FQ=(-1-1)2+322=52.
又因为点E在x轴上方,所以点E的坐标为(-1,4).
因为点P在EF的垂直平分线上,所以PE=PF.
又因为点P在抛物线上,所以PE与准线x=-1垂直.
所以点P的纵坐标为4,代入抛物线的方程得点P的坐标为(4,4),
则S△PEF=12×4×[4-(-1)]=10,故选B.
答案:B
21.(2015江西重点中学盟校联考,文7,抛物线的几何性质,选择题)双曲线x23-16y2p2=1(p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离心率为( )
A.43 B.3 C.233 D.4
解析:依题意得-3+p216=-p2(p>0),解得p=4,
所以离心率e=23=233,故选C.
答案:C
22.(2015河北石家庄二检,文13,抛物线的几何性质,填空题)已知抛物线C:y2=ax的焦点到其准线的距离为2,则实数a的值为 .
解析:利用抛物线的基本量求解.
因为抛物线y2=ax的焦点a4,0到准线x=-a4的距离|a|2=2,所以a=±4.
答案:±4
142
直线与抛物线的位置关系
1.(2015宁夏银川二中一模,文11,直线与抛物线的位置关系,选择题)已知抛物线的方程为y2=4x,过其焦点F的直线l与抛物线交于A,B两点,若S△AOF=3S△BOF(O为坐标原点),则|AB|=( )
A.163 B.83 C.43 D.4
解析:设A(x1,y1),B(x2,y2),
设直线AB的方程为x=my+1,
不妨设直线AB的倾斜角为锐角,
因为S△AOF=3S△BOF,故y1=-3y2(y1>0).①
联立x=my+1,y2=4x,消去x得y2-4my-4=0,
故y1+y2=4m,②
y1y2=-4,③
联立①②③,解得y1=23,y2=-233,m=33,
故|AB|=1+m2|y1-y2|=163,故选A.
答案:A
2.(2015东北三省四市二联,文10,直线与抛物线的位置关系,选择题)已知抛物线C:y2=4x的焦点为F,直线y=3(x-1)与C交于A,B两点(A在x轴上方).若AF=mFB,则m的值为( )
A.3 B.32 C.2 D.3
解析:求出点A,B的坐标,利用向量的坐标运算建立方程求解.
联立直线y=3(x-1)和抛物线C:y2=4x,
解得A(3,23),B13,-233,
又抛物线C的焦点F(1,0),
所以AF=(-2,-23),FB=-23,-233.
则由AF=mFB得m=3,故选D.
答案:D
3.(2015河南适应性模拟练习,文10,直线与抛物线的位置关系,选择题)过定点C(0,p)的直线与抛物线x2=2py(p>0)相交于A,B两点,若点N是点C关于坐标原点的对称点,则△ANB面积的最小值为( )
A.22p B.2p
C.22p2 D.2p2
解析:设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+p,与x2=2py联立得x2-2pkx-2p2=0,所以x1+x2=2pk,x1x2=-2p2,|AB|=1+k2(x1+x2)2-4x1x2=1+k24p2k2+8p2=2p1+k2·k2+2,点N(0,-p)到y=kx+p的距离d=2p1+k2,所以S△ANB=12d|AB|=2p2k2+2,当k=0时,(S△ANB)min=22p2,故选C.
答案:C
4.(2015东北三省三校二联,文16,直线与抛物线的位置关系,填空题)已知点A-12,12在抛物线C:y2=2px(p>0)的准线上,点M,N在抛物线C上,且位于x轴的两侧,O是坐标原点,若OM·ON=3,则点A到动直线MN的最大距离为 .
解析:依题意得p=1,抛物线C:y2=2x.
设直线MN:x=my+n,点My122,y1,Ny222,y2,其中y1y2<0,
则有y12y224+y1y2=3(y1y2<0),解得y1y2=-6.
由x=my+n,y2=2x消去x得y2-2my-2n=0,y1y2=-2n=-6,n=3,
因此直线MN:x=my+3过定点E(3,0),点A到直线MN的最大距离等于|AE|=522.
答案:522
5.(2015河南平顶山、许昌、新乡二调,文15,直线与抛物线的位置关系,填空题)已知抛物线C:y2=4x与点M(-1,1),过C的焦点且斜率为k的直线与C交于A,B两点,若MA·MB=0,则k= .
解析:利用数量积的坐标运算求解.
设A(x1,y1),B(x2,y2),直线AB:y=k(x-1),代入抛物线方程,
整理得k2x2-(2k2+4)x+k2=0,
则x1+x2=2+4k2,x1x2=1.①
MA·MB=(x1+1,y1-1)·(x2+1,y2-1)=(x1+1)(x2+1)+(kx1-k-1)(kx2-k-1)=0,
即(k2+1)x1x2+(-k2-k+1)(x1+x2)+1+(k+1)2=0,将①代入解得k=2.
答案:2
6.(2015吉林长春质量监测(二),文14,直线与抛物线的位置关系,填空题)过抛物线y2=4x的焦点作倾斜角为45°的直线l交抛物线于A,B两点,O为坐标原点,则△OAB的面积为 .
解析:抛物线焦点为(1,0),直线l的方程为y=x-1,与抛物线方程联立y=x-1,y2=4x得两交点纵坐标差的绝对值为42,从而△OAB的面积为22.
答案:22
7.(2015贵州适应性考试,文16,直线与抛物线的位置关系,填空题)设A是抛物线y2=8x上一点,F是抛物线的焦点,直线FA与抛物线准线的交点B在x轴上方.如果|AB|=2|AF|,则点A的坐标为 .
解析:分两种情况求解.
当点A在x轴上方时,过点A作抛物线准线的垂线,垂足为C,则|AB|=2|AC|,∠BAC=60°,直线AF的倾斜角为120°,此时直线AF的方程为y=-3(x-2),与抛物线方程联立解得A23,433;
当点A在x轴下方时,|AB|=2|AF|,即点F是线段AB的中点,则xA+xB=2xF,解得xA=6,代入抛物线解得yA=-43,此时A(6,-43).
综上可得点A的坐标为23,433或(6,-43).
答案:23,433或(6,-43)
143
轨迹方程
1.(本小题满分12分)(2015东北三校一联,文20,轨迹与轨迹方程,解答题)在平面直角坐标系xOy中,已知动圆过点(2,0),且被y轴所截得的弦长为4.
(1)求动圆圆心的轨迹C1的方程;
(2)过点P(1,2)分别作斜率为k1,k2的两条直线l1,l2,交C1于A,B两点(点A,B异于点P),若k1+k2=0,且直线AB与圆C2:(x-2)2+y2=12相切,求△PAB的面积.
解:(1)设动圆圆心坐标为(x,y),半径为r,
由题意得(x-2)2+y2=r2,22+x2=r2,即y2=4x,
∴动圆圆心的轨迹方程为y2=4x.(4分)
(2)设直线l1斜率为k,
则l1:y-2=k(x-1),l2:y-2=-k(x-1).
联立y2=4x,y-2=k(x-1),消去x得ky2-4y+8-4k=0.
设A(x1,y1),B(x2,y2).
由题意得Δ>0恒成立,即(k-1)2>0,∴k≠1.
∴y1yP=8-4kk.
∵yP=2,∴y1=4-2kk.
代入直线方程可得x1=(k-2)2k2,(6分)
同理可得x2=(2+k)2k2,y2=4+2k-k,(7分)
则kAB=y2-y1x2-x1=4+2k-k-4-2kk(k+2)2-(k-2)2k2=-1,(9分)
不妨设lAB:y=-x+b.
∵直线AB与圆C相切,
∴|b-2|2=22,解得b=3或b=1.
当b=3时,直线AB过点P,舍去;
当b=1时,由y=-x+1,y2=4x得x2-6x+1=0,
|AB|=1+1·32=8,
点P到直线AB的距离为d=2,
∴△PAB的面积为42.(12分)
2.(本小题满分12分)(2015山西四校三联,文20,轨迹与轨迹方程,解答题)已知点A(1,0),点P是圆C:(x+1)2+y2=8上的任意一点,线段PA的垂直平分线与直线CP交于点E.
(1)求点E的轨迹方程;
(2)若直线y=kx+m与点E的轨迹有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
解:(1)由题意知|EP|=|EA|,|CE|+|EP|=22,
∴|CE|+|EA|=22>2=|CA|.
∴点E的轨迹分别是以C,A为焦点的椭圆,
其轨迹方程为x22+y2=1.(4分)
(2)设P(x1,y1),Q(x2,y2),
则将直线与椭圆的方程联立得y=kx+m,x2+2y2=2,
消去y,整理得(2k2+1)x2+4kmx+2m2-2=0.
由题意可知Δ>0,即m2<2k2+1,(*)
x1+x2=-4km2k2+1,x1x2=2m2-22k2+1.(6分)
∵O在以PQ为直径的圆的内部,
故OP·OQ<0,即x1x2+y1y2<0,(7分)
而y1y2=(kx1+m)(kx2+m)=m2-2k22k2+1,
由x1x2+y1y2=2m2-22k2+1+m2-2k22k2+1<0,(9分)
得m2<2k2+23,∴m2<23,且满足(*)式.
故m的取值范围是-63,63.(12分)
144
圆锥曲线中的范围、最值问题
1.(本小题满分12分)(2015河南十校测试(四),文21,圆锥曲线中的范围、最值问题,解答题)定圆M:(x+3)2+y2=16,动圆N过点F(3,0)且与圆M相切,记圆心N的轨迹为E.
(1)求轨迹E的方程;
(2)设点A,B,C在E上运动,A与B关于原点对称,且|AC|=|CB|,当△ABC的面积最小时,求直线AB的方程.
解:(1)因为点F(3,0)在圆M:(x+3)2+y2=16内,
所以圆N内切于圆M.
因为|NM|+|NF|=4>|FM|,
所以点N的轨迹E为椭圆,且2a=4,c=3,
所以b=1.
所以轨迹E的方程为x24+y2=1.(4分)
(2)①当AB为长轴(或短轴)时,依题意知,点C就是椭圆的上下顶点(或左右顶点),此时S△ABC=12×|OC|×|AB|=2.(5分)
②当直线AB的斜率存在且不为0时,设其斜率为k,
则直线AB的方程为y=kx,
联立方程x24+y2=1,y=kx,得xA2=41+4k2,yA2=4k21+4k2,
所以|OA|2=xA2+yA2=4(1+k2)1+4k2.(7分)
由|AC|=|CB|知△ABC为等腰三角形,O为AB的中点,OC⊥AB,
所以直线OC的方程为y=-1kx,
由x24+y2=1,y=-1kx,
解得xC2=4k2k2+4,yC2=4k2+4,|OC|2=4(1+k2)k2+4,(9分)
S△ABC=2S△OAC=|OA|×|OC|
=4(1+k2)1+4k2×4(1+k2)k2+4=4(1+k2)(1+4k2)(k2+4) .
由于(1+4k2)(k2+4)
≤(1+4k2)+(k2+4)2=5(1+k2)2,
所以S△ABC≥85.(11分)
当且仅当1+4k2=k2+4,即k=±1时等号成立,此时△ABC面积的最小值是85.
因为2>85,所以△ABC面积的最小值为85,此时直线AB的方程为y=x或y=-x.
2.(本小题满分12分)(2015江西九校联合考试,文21,圆锥曲线中的范围、最值问题,解答题)如图,已知抛物线C:y2=2px和☉M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与☉M相切于A,B两点,分别交抛物线于E,F两点,圆心点M到抛物线准线的距离为174.
(1)求抛物线C的方程;
(2)当∠AHB的角平分线垂直x轴时,求直线EF的斜率;
(3)若直线AB在y轴上的截距为t,求t的最小值.
解:(1)∵点M到抛物线准线的距离为4+p2=174.
∴p=12,即抛物线C的方程为y2=x.(4分)
(2)∵当∠AHB的角平分线垂直x轴时,点H(4,2),
∴kHE=-kHF.
设E(x1,y1),F(x2,y2),
∴yH-y1xH-x1=-yH-y2xH-x2,∴yH-y1yH2-y12=-yH-y2yH2-y22,
∴y1+y2=-2yH=-4.
kEF=y2-y1x2-x1=y2-y1y22-y12=1y2+y1=-14.(8分)
(3)设A(x1,y1),B(x2,y2),
∵kMA=y1x1-4,∴kHA=4-x1y1.
可得,直线HA的方程为(4-x1)x-y1y+4x1-15=0,
同理,直线HB的方程为(4-x2)x-y2y+4x2-15=0,
∴(4-x1)y02-y1y0+4x1-15=0,
(4-x2)y02-y2y0+4x2-15=0.
∴直线AB的方程为(4-x)y02-y0y+4x-15=0.
令x=0,可得t=4y0-15y0(y0≥1),
∵t关于y0的函数在[1,+∞)上单调递增,
∴tmin=-11.(12分)
4.(本小题满分12分)(2015江西三校联考,文20,圆锥曲线中的范围、最值问题,解答题)设抛物线C:x2=2py(p>0)的准线被圆O:x2+y2=4所截得的弦长为15.
(1)求抛物线C的方程;
(2)设点F是抛物线C的焦点,N为抛物线C上的一动点,过N作抛物线C的切线交圆O于P,Q两点,求△FPQ面积的最大值.
解:(1)因为抛物线C的准线方程为y=-p2,且直线y=-p2被圆O:x2+y2=4所截得的弦长为15,
所以p22=4-1522,解得p=1,
因此抛物线C的方程为x2=2y.(4分)
(2)设Nt,t22,由于y'=x知直线PQ的方程为y-t22=t(x-t),即y=tx-t22.(6分)
因为圆心O到直线PQ的距离为t221+t2,
所以|PQ|=24-t44(1+t2).(7分)
设点F到直线PQ的距离为d,则d=12+t221+t2,(8分)
所以△FPQ的面积S=12|PQ|·d=1+t22·4-t44(1+t2)
=14-t4+16t2+16=14-(t2-8)2+80
≤1480=5,(11分)
当t=±22时取到“=”,经检验此时直线PQ与圆O相交,满足题意.
综上可知,△FPQ的面积的最大值为5.(12分)
5.(本小题满分12分)(2015江西南昌一模,文20,圆锥曲线中的范围、最值问题,解答题)已知圆E:x2+y-122=94经过椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线.直线l交椭圆C于M,N两点,且MN=λOA(λ≠0).
(1)求椭圆C的方程;
(2)当三角形AMN的面积取到最大值时,求直线l的方程.
解:(1)如图,圆E经过椭圆C的左、右焦点F1,F2,
∵F1,E,A三点共线,∴F1A为圆E的直径,∴AF2⊥F1F2.
∵x2+0-122=94,∴x=±2,∴c=2.(2分)
|AF2|2=|AF1|2-|F1F2|2=9-8=1,2a=|AF1|+|AF2|=4.
∵a2=b2+c2,解得a=2,b=2,(4分)
∴椭圆C的方程x24+y22=1.(5分)
(2)点A的坐标(2,1),∵MN=λOA(λ≠0),
∴直线l的斜率为22.(6分)
故设直线l的方程为y=22x+m.
y=22x+m,x24+y22=1,∴x2+2mx+m2-2=0.
设M(x1,y1),N(x2,y2),∴x1+x2=-2m,x1x2=m2-2,
Δ=2m2-4m2+8>0,∴-20)的一条直径是椭圆C2:x2a2+y2b2=1(a>b>0)的长轴,过椭圆C2上一点D1,32的动直线l与圆C1相交于点A,B,弦AB长的最小值是3.
(1)求圆C1和椭圆C2的方程;
(2)椭圆C2的右焦点为F,过点F作两条互相垂直的直线m,n,设直线m交圆C1于点P,Q,直线n交椭圆C2于点M,N,求四边形PMQN面积的取值范围.
解:(1)当l垂直于OD时|AB|最小,
因为|OD|=1+94=132,
所以r=134+322=2.(2分)
因为圆C1:x2+y2=r2(r>0)的一条直径是椭圆C2的长轴,所以a=2.
又点D在椭圆C2:x2a2+y2b2=1(a>b>0)上,
所以14+94b2=1⇒b=3.
所以圆C1的方程为x2+y2=4,椭圆C2的方程为x24+y23=1.(5分)
(2)椭圆C2的右焦点F的坐标是(1,0),
当直线m垂直于x轴时,|PQ|=23,|MN|=4,四边形PMQN的面积S=43,
当直线m垂直于y轴时,|PQ|=4,|MN|=3,四边形PMQN的面积S=6,(6分)
当直线m不垂直于坐标轴时,设n的方程为y=k(x-1)(k≠0),此时直线m的方程为y=-1k(x-1),
圆心O到直线m的距离为d=1k2+1,
所以|PQ|=2r2-d2=24k2+3k2+1,(8分)
将直线n的方程代入椭圆C2的方程得到(4k2+3)x2-8k2x+4k2-12=0,
|MN|=(1+k2)8k24k2+32-4×4k2-124k2+3.
所以四边形PMQN的面积
S=12|PQ|·|MN|=64k44k2+3-16k2+48
=-48k24k2+3+48
=43·-14+3k2+1∈(6,43),
综上,四边形PMQN的面积的取值范围是[6,43].(12分)
7.(本小题满分12分)(2015东北三省四市二联,文20,圆锥曲线中的范围、最值问题,解答题)已知椭圆C:x2a2+y2b2=1(a>b>0)的上顶点为(0,2),且离心率为32.
(1)求椭圆C的方程;
(2)证明:过圆x2+y2=r2上一点Q(x0,y0)的切线方程为x0x+y0y=r2;
(3)从椭圆C上一点P向圆x2+y2=1引两条切线,切点分别为A,B,直线AB分别与x轴、y轴交于M,N两点,求|MN|的最小值.
(1)解:由题可知b=2,(1分)
e=ca=32,∴a=4,c=23.(3分)
∴椭圆C的方程为x216+y24=1.(4分)
(2)证明:当切线的斜率k存在时,
设切线的方程为y-y0=k(x-x0).
又因为k=-x0y0,(5分)
故切线的方程为y-y0=-x0y0(x-x0),
∴x0x+y0y=r2.(6分)
当k不存在时,切点的坐标为(±r,0),
切线的方程为x=±r,符合x0x+y0y=r2,(7分)
综上所述,切线的方程为x0x+y0y=r2.(8分)
(3)解:设点P的坐标为(xP,yP),PA,PB是圆x2+y2=1的切线,切点A(x1,y1),B(x2,y2),
由(2)可知过点A的圆的切线为x1x+y1y=1,过点B的圆的切线为x2x+y2y=1,
∵两切线都过P点,
∴x1xP+y1yP=1,x2xP+y2yP=1.
∴切点弦AB的方程为xPx+yPy=1,(9分)
由题知xPyP≠0,∴M1xP,0,N0,1yP,(10分)
∴|MN|2=1xP2+1yP2=1xP2+1yP2·xP216+yP24
=116+14+116·xP2yP2+14·yP2xP2
≥116+14+2164·xP2yP2·yP2xP2
=916,
当且仅当xP2=163,yP2=83时取等号,(11分)
∴|MN|≥34,∴|MN|的最小值为34.(12分)
8.(本小题满分12分)(2015山西太原二模,文20,圆锥曲线中的范围、最值问题,解答题)已知动点A在椭圆C:y2a2+x2b2=1(a>b>0)上,动点B在直线x=-2上,且满足OA⊥OB(O为坐标原点),椭圆C上的点M32,3到两焦点距离之和为43.
(1)求椭圆C的方程;
(2)求|AB|取最小值时点A的坐标.
解:(1)由题意得2a=43,9a2+34b2=1,∴a2=12,b2=3.
∴椭圆C的方程为y212+x23=1.(4分)
(2)由题意可设A(x0,y0),B(-2,t)(t∈R),
∵OA⊥OB,∴2x0=ty0,∴t=2x0y0.
∵动点A在椭圆C上,∴y0212+x023=1.
∴x02=3-14y02.(6分)
∴|AB|=(x0+2)2+(y0-t)2
=x02+4x0+4+y02-2ty0+t2(7分)
=x02+y02+4x02y02+4=6+34y02+12y02≥23.(10分)
当且仅当34y02=12y02,即y0=±2时,|AB|取最小值,
∵x02=3-14y02,∴x0=±2.
∴点A的坐标为(2,-2),(2,2),(-2,-2)或(-2,-2).(12分)
9.(本小题满分12分)(2015河北石家庄一模,文20,圆锥曲线中的范围、最值问题,解答题)在平面直角坐标系xOy中,一动圆经过点(1,0)且与直线x=-1相切,若该动圆圆心的轨迹为曲线E.
(1)求曲线E的方程;
(2)已知点A(m,0),倾斜角为π4的直线l与线段OA相交(不经过点O或点A)且与曲线E交于M,N两点,求△AMN面积的最大值及此时直线l的方程.
解:(1)由题意可知圆心到(1,0)的距离等于到直线x=-1的距离,由抛物线的定义可知圆心的轨迹方程为y2=4x.(4分)
(2)由题意可设l的方程为y=x-m,其中00成立.
设M(x1,y1),N(x2,y2),
则x1+x2=4+2m,x1·x2=m2,(6分)
∴|MN|=1+k2|x1-x2|=42+2m.
又∵点A到直线l的距离为d=5-m2,
∴S△AMN=2(5-m)1+m
=2m3-9m2+15m+25.(9分)
令f(m)=m3-9m2+15m+25(0b>0)的左、右焦点分别为F1和F2,上顶点为B,BF2的延长线交椭圆于点A,△ABF1的周长为8,且BF1·BA=0.
(1)求椭圆C的方程;
(2)若直线l⊥AB且与椭圆C相交于两点P,Q,求|PQ|的最大值.
解:(1)由椭圆的定义得△ABF1的周长为4a,
∴4a=8,a=2.
又顶点B(0,b),焦点F1(-c,0)和F2(c,0),且BF1·BA=0,即(-c,-b)·(c,-b)=0,∴b=c.
又b2+c2=a2=4,∴b=c=2,
∴椭圆的方程为x24+y22=1.(6分)
(2)由(1)知B(0,2),F2(2,0),直线AB的斜率kAB=-1,
∵l⊥AB,则直线l的斜率kl=1,设直线l的方程为y=x+t,
代入椭圆方程x24+y22=1得3x2+4tx+2t2-4=0,
Δ=-8t2+48>0,即-60恒成立.
所以t∈R,对于上式,当t=0时,(OM·ON)max=14.
综上所述,OM·ON的最大值为14.(12分)
12.(本小题满分12分)(2015河北石家庄二检,文20,圆锥曲线中的范围、最值问题,解答题)已知椭圆C1:x24b2+y2b2=1(b>0),抛物线C2:y=14x2+b,过点F(0,b+1)作x轴的平行线,与抛物线C2在第一象限的交点为G,且该抛物线在点G处的切线经过坐标原点O.
(1)求椭圆C1的方程;
(2)设直线l:y=kx与椭圆C1相交于C,D两点,其中点C在第一象限.点A,B为椭圆C1的右顶点和上顶点,求四边形ACBD面积的最大值.
解:(1)由y=14x2+b可知当y=b+1时,得x=±2,
∴G点的坐标为(2,b+1),则y'=12x,y'|x=2=1,(2分)
过点G的切线方程为y-(b+1)=x-2,
即y=x+b-1.
令y=0,得x=1-b=0,∴b=1.
∴椭圆的方程为x24+y2=1.(4分)
(2)依题意有k>0,设C(xC,kxC),
由x24+y2=1,y=kx得(1+4k2)x2-4=0.
∴xC=21+4k2,yC=2k1+4k2,|CD|=41+k21+4k2.(6分)
点A到CD的距离为h1=2k1+k2,
点B到CD的距离为h2=11+k2,(8分)
S四边形ACBD=12×|CD|×(h1+h2)
=2(2k+1)1+4k2=2(2k+1)21+4k2
=21+4k2+4k1+4k2=21+114k+k≤22,(10分)
当且仅当14k=k,即当k=12时,等号成立.
所以S四边形ACBD的最大值为22.(12分)
14.(本小题满分12分)(2015山西太原模拟(一),文20,圆锥曲线中的范围、最值问题,解答题)已知椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别是点F1,F2,其离心率e=12,点P为椭圆上的一个动点,△PF1F2面积的最大值为43.
(1)求椭圆的方程;
(2)若A,B,C,D是椭圆上不重合的四个点,AC与BD相交于点F1,AC·BD=0,求|AC|+|BD|的取值范围.
解:(1)由题意得,当点P是椭圆的上、下顶点时,△PF1F2面积取最大值,此时S△PF1F2=12·|F1F2|·|OP|=bc,∴bc=43.(2分)
∵e=12,∴b=23,a=4.(5分)
∴椭圆的方程为x216+y212=1.(6分)
(2)由(1)得椭圆的方程为x216+y212=1,则F1的坐标为(-2,0),
∵AC·BD=0,∴AC⊥BD.(7分)
①当直线AC与BD中有一条直线斜率不存在时,易得|AC|+|BD|=6+8=14;
②当直线AC斜率k存在且k≠0时,则其方程为y=k(x+2),
设A(x1,y1),C(x2,y2),则点A,C的坐标是方程组y=k(x+2),x216+y212=1的两组解,
∴(3+4k2)x2+16k2x+16k2-48=0,
∴x1+x2=-16k23+4k2,x1x2=16k2-483+4k2,
∴|AC|=1+k2|x1-x2|=24(k2+1)3+4k2,(9分)
此时直线BD的方程为y=-1k(x+2),
同理,由y=-1k(x+2),x216+y212=1,可得|BD|=24(k2+1)3k2+4,
∴|AC|+|BD|=24(k2+1)4k2+3+24(k2+1)3k2+4=168(k2+1)2(3k2+4)(4k2+3).
令t=k2+1(k≠0),则t>1,
∴|AC|+|BD|=16812+t-1t2.
∵t>1,∴00)相切,并与M的轨迹相交于A,B两点,以AB为直径的圆恒过圆C2的圆心,当r值最大时,求直线l的方程.
解:(1)易知M的轨迹为顶点在原点,焦点为(1,0)的抛物线,所以M的轨迹方程为y2=4x.(4分)
(2)设直线l的方程为my=x+t,则有|t|1+m2=r.
联立my=x+t,y2=4x⇒y2-4my+4t=0,
Δ=16m2-16t>0,得m2>t.
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1·y2=4t,(7分)
x1x2=(my1-t)(my2-t)=m2y1y2-mt(y1+y2)+t2=4m2t-4m2t+t2=t2.
∵以AB为直径的圆恒过圆C2的圆心,
∴OA⊥OB,x1x2+y1y2=0,
t2+4t=0,t=-4或t=0(舍去),(10分)
r=41+m2,当m=0时,rmax=4.
此时直线l的方程为x=4.(12分)
16.(本小题满分12分)(2015贵州贵阳监测考试(一),文20,圆锥曲线中的范围、最值问题,解答题)已知两点F1(-1,0)及F2(1,0),点P在以F1,F2为焦点的椭圆C上,且|PF1|+|PF2|=4.(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l,求四边形F1MNF2面积S的最大值.
解:(1)依题意,设椭圆C的方程为x2a2+y2b2=1(a>b>0).
∵|PF1|+|PF2|=4,∴a=2.
又∵c=1,∴b2=3.
∴椭圆C的方程为x24+y23=1.(6分)
(2)将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中,
得(4k2+3)x2+8kmx+4m2-12=0.
由直线l与椭圆C仅有一个公共点知,
Δ=64k2m2-4(4k2+3)(4m2-12)=0,
化简得m2=4k2+3.
设d1=|F1M|=|-k+m|k2+1,d2=|F2M|=|k+m|k2+1,
当k≠0时,设直线l的倾斜角为θ,
则|d1-d2|=|MN|×|tan θ|,
∴|MN|=d1-d2k,
S四边形F1MNF2=12d1-d2k(d1+d2)
=d12-d222k=2|m|k2+1
=2|m|m2-34+1=8|m|+1|m|,
∴m2=4k2+3.
∴当k≠0时,|m|>3,|m|+1|m|>3+13=433,S<23.
当k=0时,四边形F1MNF2是矩形,S=23.
∴四边形F1MNF2面积S的最大值为23.(12分)
145
圆锥曲线中的定值、定点问题
1.(本小题满分12分)(2015宁夏银川二中一模,文20,圆锥曲线中的定值、定点问题,解答题)已知椭圆C:x2a2+y2b2=1(a>b>0)过点(2,0),且椭圆C的离心率为12.
(1)求椭圆C的方程;
(2)若动点P在直线x=-1上,过点P作直线交椭圆C于M,N两点,且P为线段MN的中点,再过点P作直线l⊥MN,则直线l是否恒过定点?若是,请求出该定点的坐标;若不是,请说明理由.
解:(1)因为点(2,0)在椭圆C上,
所以4a2+0b2=1,所以a2=4.(1分)
因为椭圆C的离心率为12,
所以ca=12,即a2-b2a2=14,(2分)
解得b2=3,所以椭圆C的方程为x24+y23=1.(4分)
(2)设P(-1,y0),y0∈-32,32,
①当直线MN的斜率存在时,设直线MN的方程为y-y0=k(x+1),M(x1,y1),N(x2,y2),
由3x2+4y2=12,y-y0=k(x+1),得(3+4k2)x2+(8ky0+8k2)x+(4y02+8ky0+4k2-12)=0,(6分)
所以x1+x2=-8ky0+8k23+4k2.
因为P为MN的中点,
所以x1+x22=-1,即-8ky0+8k23+4k2=-2.
所以kMN=34y0(y0≠0),(8分)
因为直线l⊥MN,所以kl=-4y03.
所以直线l的方程为y-y0=-4y03(x+1),
即y=-4y03x+14,
显然直线l恒过定点-14,0.(10分)
②当直线MN的斜率不存在时,直线MN的方程为x=-1,
此时直线l为x轴,也过点-14,0.
综上所述,直线l恒过定点-14,0.(12分)
2.(本小题满分12分)(2015贵州适应性考试,文20,圆锥曲线中的定值、定点问题,解答题)已知椭圆C的中心是坐标原点O,长轴在x轴上,且经过点1,32,C上任意一点到两个焦点的距离之和为4.
(1)椭圆C的标准方程;
(2)已知M,N是椭圆C上的两点,且OM⊥ON,求证:1|OM|2+1|ON|2为定值.
(1)解:由已知得2a=4,a=2.(1分)
设椭圆C的方程为x24+y2b2=1(00,则x1+x2=-x0y0,x1x2=-1-1y0,
所以OM·ON=x1x2+y1y2=x1x2+(x12-1)(x22-1)
=x1x2+x12x22-(x12+x22)+1
=x1x2+(x1x2)2-[(x1+x2)2-2x1x2]+1
=-1-1y0+1+1y02-x02y02+2+2y0+1
=-1y0<0,
从而∠MON为钝角.(12分)
4.(本小题满分12分)(2015吉林长春质量监测(二),文20,圆锥曲线中的定值、定点问题,解答题)在△ABC中,顶点B(-1,0),C(1,0),G,I分别是△ABC的重心和内心,且IG∥BC.
(1)求顶点A的轨迹M的方程;
(2)过点C的直线交曲线M于P,Q两点,H是直线x=4上一点,设直线CH,PH,QH的斜率分别为k1,k2,k3,求证:2k1=k2+k3.
(1)解:已知S△ABC=12(|AB|+|AC|+|BC|)·r=12|BC|·|yA|,
且|BC|=2,|yA|=3r,其中r为内切圆半径,化简得|AB|+|AC|=4,顶点A的轨迹是以B,C为焦点,4为长轴长的椭圆(去掉长轴端点),其中a=2,c=1,b=3,其方程为x24+y23=1(y≠0).(5分)
(2)证明:当直线PQ斜率存在时,
设直线PQ:y=k(x-1)且P(x1,y1),Q(x2,y2),H(4,m).
联立x24+y23=1,y=k(x-1)可得x1+x2=8k23+4k2,x1x2=4k2-123+4k2.(8分)
由题意知k1=m3,k2=y1-mx1-4,k3=y2-mx2-4.
k2+k3=(y1-m)(x2-4)+(y2-m)(x1-4)(x1-4)(x2-4)
=8m+8k+2kx1x2-(m+5k)(x1+x2)x1x2-4(x1+x2)+16
=24mk2+24m36k2+36=2m3=2k1.
当直线PQ斜率不存在时,P1,32,Q1,-32,
k2+k3=m-323+m+323=2m3=2k1.
综上可得2k1=k2+k3.(12分)
5.(本小题满分12分)(2015甘肃第二次诊断考试,文20,圆锥曲线中的定值、定点问题,解答题)椭圆C:x2a2+y2b2=1(a>b>0)的离心率e=12,原点到过椭圆右焦点F且斜率是1的直线l的距离为22.
(1)求椭圆C的方程;
(2)已知A,B为椭圆长轴的两个端点,作不平行于坐标轴且不经过右焦点F的割线PQ,若满足∠AFP=∠BFQ,求证:割线PQ恒经过一定点.
(1)解:依题意可设l:y=x-c,则22=c2,解得c=1,
又e=12,所以a=2,b=3.
于是椭圆C的方程为x24+y23=1.(5分)
(2)证明:设P(x1,y1),Q(x2,y2),且割线PQ的方程为y=kx+m(k≠0),
由x24+y23=1,y=kx+m⇒(3+4k2)x2+8kmx+4m2-12=0,
所以x1+x2=-8km3+4k2,x1x2=4m2-123+4k2,(*)
由∠AFP=∠BFQ,得kPF=-kQF⇒y1x1-1+y2x2-1=0
⇒y1(x2-1)+y2(x1-1)=0,
即2kx1x2+(m-k)(x1+x2)-2m=0,
将(*)式代入上式得2k4m2-123+4k2+(m-k)-8km3+4k2-2m=0,
化简得m=-4k,(10分)
所以割线PQ的方程为y=k(x-4),
所以割线PQ恒经过一定点(4,0).(12分)
6.(本小题满分12分)(2015山西大附中第五次月考,文20,圆锥曲线中的定值、定点问题,解答题)已知抛物线的顶点在坐标原点O,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.直线l:y=kx+b与抛物线交于B,C两点.
(1)求抛物线的方程;
(2)当直线OB,OC的倾斜角之和为45°时,证明直线l过定点.
(1)解:设抛物线方程为y2=2px(p>0),
由抛物线的定义知|AF|=1+p2,
又|AF|=2,所以p=2.
所以抛物线的方程为y2=4x.(4分)
(2)证明:设By124,y1,Cy224,y2,
联立y2=4x,y=kx+b,消去x整理得ky2-4y+4b=0,显然k≠0,
所以y1+y2=4k,y1y2=4bk.
设直线OB,OC的倾斜角分别为α,β,斜率分别为k1,k2,
则α+β=45°,tan(α+β)=k1+k21-k1k2=tan 45°=1,
其中k1=y1x1=4y1,k2=4y2,
代入上式整理得y1y2-16-4(y1+y2)=0,
将y1+y2=4k,y1y2=4bk代入,
得4bk-16=16k,即b=4k+4,
则直线l的方程为y=kx+4k+4,
整理得y-4=k(x+4),
所以直线l过定点(-4,4).(12分)
7.(本小题满分12分)(2015河南洛阳3月统一考试,文20,圆锥曲线中的定值、定点问题,解答题)设M是焦距为2的椭圆E:x2a2+y2b2=1(a>b>0)上一点,A,B是椭圆E的左、右顶点,直线MA与MB的斜率分别为k1,k2,且k1k2=-12.
(1)求椭圆E的方程;
(2)已知椭圆E:x2a2+y2b2=1(a>b>0)上点N(x0,y0)处的切线方程为x0xa2+y0yb2=1.若P是直线x=2上任意一点,从点P向椭圆E作切线,切点分别为C,D,求证:直线CD恒过定点,并求出该定点坐标.
(1)解:由题意得2c=2,c=1,A(-a,0),B(a,0),设M(x,y),
∵k1k2=-12,∴yx+a·yx-a=-12,
即y2x2-a2=-12.
∵M(x,y)在椭圆E上,∴x2a2+y2b2=1.
∴b21-x2a2x2-a2=-12,∴b2a2=12,∴a2=2b2.(3分)
又a2-b2=c2=1,∴a2=2,b2=1.
∴椭圆E的方程为x22+y2=1.(5分)
(2)证明:设切点坐标为C(x1,y1),D(x2,y2),P(2,t),切线方程分别为x1x2+y1y=1,x2x2+y2y=1.(7分)
∵两切线均过点P,
∴2x12+ty1=1,2x22+ty2=1.
即x1+ty1=1,x2+ty2=1.
∴直线CD的方程为x+ty=1.(10分)
对于任意实数t,点(1,0)都适合这个方程,即直线CD恒过定点(1,0).(12分)
8.(本小题满分12分)(2015江西赣州摸底考试,文20,圆锥曲线中的定值、定点问题,解答题)已知椭圆E:x2a2+y2b2=1(a>b>0)的焦距为2,A是E的右顶点,P,Q是E上关于原点对称的两点,且直线PA的斜率与直线QA的斜率之积为-34.
(1)求E的方程;
(2)过E的右焦点作直线l与E交于M,N两点,直线MA,NA与直线x=3分别交于C,D两点,设△ACD与△AMN的面积分别记为S1,S2,且S1·S2=187,求直线l的方程.
解:(1)设P(x0,y0),Q(-x0,-y0),
则y02=b2a2(a2-x02),(1分)
kPA·kQA=y0x0-a·y0x0+a=y02x02-a2=-b2a2,
依题意有b2a2=34.
又c=1,所以解得a2=4,b2=3,
故E的方程为x24+y23=1.(5分)
(2)设直线MN的方程为x=my+1,
代入E的方程得(3m2+4)y2+6my-9=0.(6分)
设M(x1,y1),N(x2,y2),
则y1+y2=-6m3m2+4,y1y2=-93m2+4,(7分)
直线MA的方程为y=y1x1-2(x-2),
把x=3代入得yC=y1x1-2=y1my1-1.
同理yD=y2my2-1,(8分)
所以|CD|=|yC-yD|=|y1-y2||m2y1y2-m(y1+y2)+1|=3m2+1.
所以S1=12|CD|=32m2+1,(9分)
S2=12|AF|·|y1-y2|=6m2+13m2+4,(10分)
S1·S2=9(m2+1)3m2+4,
所以9(m2+1)3m2+4=187,解得m=±1,(11分)
故直线l的方程为x+y-1=0或x-y+1=0.(12分)
9.(本小题满分12分)(2015河南高考适应性测试,文21,圆锥曲线中的定值、定点问题,解答题)已知A1,A2,F1,F2分别是椭圆E:x2a2+y2b2=1(a>b>0)的左、右顶点和左、右焦点,过F2引一条直线与椭圆交于M,N两点,△MF1N的周长为8,且|F2A2|=1.
(1)求椭圆E的方程;
(2)过点P(-3,0)且斜率不为零的直线l与椭圆交于不同的两点A,B,C,D为椭圆上不同于A,B的另外两点,满足AF2=λF2C,BF2=μF2D,且λ+μ=132,求直线l的方程.
解:(1)由椭圆定义知,4a=8,即a=2.(1分)
由|F2A2|=1得a-c=1,
所以c=1,从而b2=a2-c2=3.(4分)
故椭圆的方程为x24+y23=1.(5分)
(2)显然直线l的斜率存在,故设其方程为y=k(x+3),
又设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由y=k(x+3),x24+y23=1得(3+4k2)x2+24k2x+36k2-12=0.
Δ=(24k2)2-4×(3+4k2)(36k2-12)>0⇒0b>0)的焦距为4,且过点A(2,3).
(1)求椭圆C的方程和离心率;
(2)过点(4,0)作直线l交椭圆C于P,Q两点,点S与P关于x轴对称,求证:直线SQ恒过定点并求出定点坐标.
(1)解:由题设得a2=b2+4,2a2+3b2=1,∴a2=8,b2=4.
故所求椭圆的方程为x28+y24=1,∴离心率为22.(4分)
(2)证明:显然直线l的斜率存在,
故设l的方程为y=k(x-4).
∵S与P关于x轴对称,∴xS=xP,yS=-yP,
联立方程x28+y24=1,y=k(x-4)⇒(2k2+1)x2-16k2x+32k2-8=0.
Δ=(-16k2)2-4(1+2k2)(32k2-8)>0,
∴-22xQ,xP-xQ=(xP+xQ)2-4xPxQ=422k2+11-2k2.
yP+yQ=k(xP+xQ-8)=-8k2k2+1,
yP-yQ=k(xP-xQ)=42k2k2+11-2k2.
kSQ=yS-yQxS-xQ=-(yP+yQ)xP-xQ=2k1-2k2.
记SQ的中点为MxS+xQ2,yS+yQ2,
即M8k22k2+1,-22k2k2+11-2k2.
∴SQ的方程为y+22k2k2+11-2k2=2k1-2k2x-8k22k2+1.
化简得y=2k1-2k2x-22k1-2k2=2k1-2k2(x-2),
∴点(2,0)在SQ上.
同理,xPb>0)的左、右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=12x的焦点,且F1B·QB=0,2F1F2+QF1=0.
(1)求椭圆C的标准方程;
(2)过定点P(0,2)的直线l与椭圆C交于M,N两点(M在P,N之间),设直线l的斜率为k(k>0),在x轴上是否存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形?若存在,求出实数m的取值范围;若不存在,请说明理由.
解:(1)由已知得Q(3,0),F1B⊥QB,|QF1|=4c=3+c,
所以c=1.(1分)
在Rt△F1BQ中,F2为线段F1Q的中点,
故|BF2|=2c=2,所以a=2.(2分)
于是椭圆C的标准方程为x24+y23=1.(4分)
(2)设直线l:y=kx+2(k>0),M(x1,y1),N(x2,y2),取MN的中点为E(x0,y0).
假设存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形,取MN的中点为E,则AE⊥MN.
由y=kx+2,x24+y23=1得(4k2+3)x2+16kx+4=0,
Δ>0⇒k2>14,又k>0,所以k>12.(6分)
因为x1+x2=-16k4k2+3,
所以x0=-8k4k2+3,y0=kx0+2=64k2+3.(8分)
因为AE⊥MN,所以kAE=-1k,
即64k2+3-0-8k4k2+3-m=-1k,
整理得m=-2k4k2+3=-24k+3k.(10分)
因为k>12,所以4k+3k≥43,14k+3k∈0,312,
所以m∈-36,0.(12分)
2.(本小题满分12分)(2015河北石家庄二中一模,文20,圆锥曲线中的存在、探索性问题,解答题)椭圆C:x2a2+y2b2=1(a>b>0)的上顶点为A,P43,b3是C上的一点,以AP为直径的圆经过椭圆C的右焦点F.
(1)求椭圆C的方程;
(2)动直线l与椭圆C有且只有一个公共点,问:在x轴上是否存在两个定点,它们到直线l的距离之积等于1?如果存在,求出这两个定点的坐标;如果不存在,请说明理由.
解:(1)F(c,0),A(0,b),由题设可知FA·FP=0,
则c2-43c+b23=0. ①(1分)
又点P在椭圆C上,∴169a2+b29b2=1,∴a2=2. ②
又b2+c2=a2=2, ③(3分)
联立①③,解得c=1,b2=1.(4分)
故所求椭圆的方程为x22+y2=1.(5分)
(2)当直线l的斜率存在时,设其方程为y=kx+m,代入椭圆方程,
消去y整理得(2k2+1)x2+4kmx+2m2-2=0,(*)
方程(*)有且只有一个实根,又2k2+1>0,
所以Δ=0,解得m2=2k2+1.(8分)
假设存在M1(λ1,0),M2(λ2,0)满足题设,
则d1·d2=|(λ1k+m)(λ2k+m)|k2+1
=|λ1λ2k2+(λ1+λ2)km+2k2+1|k2+1
=(λ1λ2+2)k2+(λ1+λ2)km+1k2+1
=1对任意的实数k恒成立,
所以λ1λ2=-1,λ1+λ2=0,解得λ1=1,λ2=-1或λ1=-1,λ2=1.
当直线l的斜率不存在时,经检验符合题意.
综上所述,存在两个定点M1(0,1),M2(-1,0),使它们到直线l的距离之积等于1.(12分)
3.(本小题满分12分)(2015江西重点中学盟校联考,文20,圆锥曲线中的存在、探索性问题,解答题)已知椭圆E:x2a2+y2b2=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,过椭圆焦点垂直于长轴的弦长为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且OA⊥OB,求出该圆的方程.
解:(1)由题知2|F1F2|=|MF1|+|MF2|,
即2×2c=2a,得a=2c.
又由2b2a=3得b2=32a,
且a2=b2+c2,解得c=1,a=2,b=3.
∴椭圆E的方程为x24+y23=1.(5分)
(2)假设以原点为圆心,r为半径的圆满足条件.
①若圆的切线的斜率存在,并设其方程为y=kx+m,
则r=|m|k2+1,r2=m2k2+1,
由x24+y23=1,y=kx+m消去y整理得(3+4k2)x2+8kmx+4(m2-3)=0,
设A(x1,y1),B(x2,y2),有x1+x2=-8km3+4k2,x1x2=4(m2-3)3+4k2.
又∵OA⊥OB,∴x1x2+y1y2=0,
即4(1+k2)(m2-3)-8k2m2+3m2+4k2m2=0,
化简得m2=127(k2+1),
由r2=m2k2+1,m2=127(k2+1),求得r2=127.
所求圆的方程为x2+y2=127.(10分)
②若AB的斜率不存在,
设A(x1,y1),则B(x1,-y1),
∵OA⊥OB,∴OA·OB=0,有x12-y12=0,x12=y12,
代入x124+y123=1,得x12=127.
此时仍有r2=|x12|=127.
综上所述,总存在以原点为圆心的圆x2+y2=127满足题设条件.(12分).
4.(本小题满分12分)(2015河南平顶山、许昌、新乡二调,文20,圆锥曲线中的存在、探索性问题,解答题)设椭圆x2a2+y2b2=1(a>b>0),过左焦点F作倾斜角为45°的直线交椭圆于A,B两点,且B(0,1).
(1)若FA=λ·FB,求λ;
(2)设AB的中垂线与椭圆交于C,D两点,问A,B,C,D四点是否共圆?若共圆,则求出该圆的方程,若不共圆,请说明理由.
解:(1)∵直线AB交椭圆于点B(0,1),∴b=1,
又直线AB的倾斜角为45°,∴c=b.
∴椭圆的方程为x22+y2=1.(2分)
将直线AB:y=x+1代入椭圆,整理得3x2+4x=0,
解得A-43,-13,B(0,1),将其代入FA=λFB,
解得λ=-13.(5分)
(2)由(1)得AB的中点为-23,13,
∴AB的中垂线CD的方程为y=-x-13.
设C(x1,y1),D(x2,y2),
将直线CD:y=-x-13代入椭圆,
整理得3x2+43x-169=0.
∵BC·BD=x1·x2+(y1-1)(y2-1)
=x1·x2+x1+43x2+43
=2x1·x2+43(x1+x2)+169
=-2×1627+43×-49+169=0.
∴BC⊥BD,∴A,B,C,D四点共圆.
∵CD的中点为-29,-19,B(0,1),
∴所求圆的半径为-29-02+-19-12=1049,
∴经过A,B,C,D四点的圆的方程为
x+292+y+192=10481.(12分)
5.(本小题满分12分)(2015河北保定一模,文20,圆锥曲线中存在、探索性问题,解答题)已知椭圆x2a2+y2b2=1(a>b>0)的短轴长为2,离心率为22,过右焦点F的直线l交椭圆于P,Q两点.
(1)求椭圆的方程;
(2)在线段OF上是否存在点M(m,0),使得(MP+MQ)·(MP-MQ)=0?若存在,求出m的取值范围;若不存在,请说明理由.
解:(1)由椭圆短轴长为2得b=1,
又e=a2-1a=22,∴a=2.
所求椭圆方程为x22+y2=1.(3分)
(2)假设在线段OF上存在点M(m,0)(0≤m≤1),
使得(MP+MQ)·(MP-MQ)=0成立,
即|MP|2-|MQ|2=0或|MP|=|MQ|.
①当l⊥x轴时,显然线段OF上的点都满足条件,此时0≤m≤1;(5分)
②当l与x轴重合时,显然只有原点满足条件,此时m=0;(6分)
③当l的斜率存在且不为零时,设直线l的方程为y=k(x-1)(k≠0),点P(x1,y1),点Q(x2,y2).
由x2+2y2=2,y=k(x-1)得(1+2k2)x2-4k2x+2k2-2=0.
∴x1+x2=4k21+2k2,x1x2=2k2-21+2k2.(8分)
MP=(x1-m,y1),MQ=(x2-m,y2),
其中x2-x1≠0,
∴(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0
⇔(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0
⇔(x1+x2-2m)+k(y1+y2)=0
⇔4k21+2k2-2m+k24k21+2k2-2=0
⇔2k2-(2+4k2)m=0⇔m=k21+2k2=12+1k2(k≠0).
∴0b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|=2(其中O为坐标原点).
(1)求椭圆的方程;
(2)若C,D分别是椭圆长轴的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P,试问x轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP,MQ的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
解:(1)由已知得b=c=2,∴a2=b2+c2=4.
∴椭圆的方程为x24+y22=1.(4分)
(2)由(1)知,C(-2,0),D(2,0).
由题意可设CM:y=k(x+2),P(x1,y1).
∵MD⊥CD,∴M(2,4k).
由x24+y22=1,y=k(x+2)消去y,
整理得(1+2k2)x2+8k2x+8k2-4=0,
∴Δ=(8k2)2-4(1+2k2)(8k2-4)>0.
-2x1=8k2-41+2k2,即x1=2-4k21+2k2.
∴y1=k(x1+2)=4k1+2k2,∴点P2-4k21+2k2,4k1+2k2.(6分)
设Q(x0,0),且x0≠-2.
若以MP为直径的圆恒过DP,MQ的交点,
则MQ⊥DP,∴QM·DP=0恒成立.
QM=(2-x0,4k),DP=-8k21+2k2,4k1+2k2.
∴QM·DP=(2-x0)·-8k21+2k2+4k·4k1+2k2=0,(10分)
即8k21+2k2x0=0恒成立,∴x0=0.
∴存在Q(0,0),使得以MP为直径的圆恒过直线DP,MQ的交点.(12分)
7.(本小题满分12分)(2015河南六市一联,文20,圆锥曲线中的存在、探索性问题,解答题)在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.
(1)若直线l过点A(4,0),且被圆C1截得的弦长为23,求直线l的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2,它们分别与圆C1和圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求所有满足条件的点P的坐标.
解:(1)设直线l的方程为y=k(x-4),即kx-y-4k=0,
由垂径定理得圆心C1到直线l的距离d=22-2322=1,
由点到直线的距离公式得|-3k-1-4k|k2+1=1,
化简得24k2+7k=0,解得k=0或k=-724,
当k=0时,直线l的方程为y=0;
当k=-724时,直线l的方程为y=-724(x-4),
即7x+24y-28=0.
∴所求直线l的方程为y=0或7x+24y-28=0.(6分)
(2)设点P的坐标为(m,n),直线l1,l2的方程分别为
y-n=k(x-m),y-n=-1k(x-m),
即kx-y+n-km=0,-1kx-y+n+1km=0.
∵直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,两圆半径相等,
∴由垂径定理得圆心C1到直线l1与圆心C2到直线l2的距离相等.
∴|-3k-1+n-km|k2+1=-4k-5+n+1km1k2+1,
化简得(2-m-n)k=m-n-3或(m-n+8)k=m+n-5.
∵关于k的方程有无穷多解,
∴2-m-n=0,m-n-3=0或m-n+8=0,m+n-5=0,
解得m=52,n=-12或m=-32,n=132,
即点P的坐标为-32,132或52,-12.(12分)
8.(本小题满分12分)(2015东北三省四市一联,文20,圆锥曲线中的存在、探索性问题,解答题)设抛物线的顶点在坐标原点,焦点F在y轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到x轴的距离是3.
(1)求抛物线的标准方程;
(2)在抛物线上是否存在不与原点重合的点P,使得过点P的直线交抛物线于另一点Q,满足PF⊥QF,且直线PQ与抛物线在点P处的切线垂直?并请说明理由.
解:(1)设抛物线的方程是x2=2py(p>0),A(xA,yA),B(xB,yB),
由抛物线定义可知yA+yB+p=8.(2分)
又AB中点到x轴的距离为3,
所以yA+yB=6,所以p=2,
所以抛物线的标准方程是x2=4y.(4分)
(2)设P(x1,y1),x1≠0,Q(x2,y2),
则x2=4y在P处的切线方程是y=x12x-y1,
直线PQ:y=-2x1x+2+y1代入x2=4y,
得x2+8x1x-4(2+y1)=0,(6分)
故x1+x2=-8x1,x1x2=-8-4y1,
所以x2=-8x1-x1,y2=4y1+y1+4.(8分)
而FP·FQ=y12-2y1-4y1-7=0,(10分)
即y13-2y12-7y1-4=0(y1>0),(y1+1)2(y1-4)=0,
所以y1=4,存在点P(±4,4).(12分)
9.(本小题满分12分)(2015甘肃兰州实战,文20,圆锥曲线中的存在、探索性问题,解答题)已知点P为y轴上的动点,点M为x轴上的动点,点F(1,0)为定点,且满足PN+12NM=0,PM·PF=0.
(1)求动点N的轨迹E的方程;
(2)过点F且斜率为k的直线l与曲线E交于两点A,B,试判断在x轴上是否存在点C,使得|CA|2+|CB|2=|AB|2成立?请说明理由.
解:(1)设N(x,y),则由PN+12NM=0,得P为MN的中点.(2分)
∴P0,y2,M(-x,0).
∴PM=-x,-y2,PF=1,-y2.
∴PM·PF=-x+y24=0,即y2=4x.
∴动点N的轨迹E的方程为y2=4x.(5分)
(2)设直线l的方程为y=k(x-1),
由y=k(x-1),y2=4x,消去x得y2-4ky-4=0.
设A(x1,y1),B(x2,y2),则y1+y2=4k,y1y2=-4.(6分)
假设存在点C(m,0)满足条件,
则CA=(x1-m,y1),CB=(x2-m,y2),
∴CA·CB=x1x2-m(x1+x2)+m2+y1y2
=y1y242-my12+y224+m2-4
=-m4[(y1+y2)2-2y1y2]+m2-3
=m2-m4k2+2-3.(9分)
∵Δ=4k2+22+12>0,
∴关于m的方程m2-m4k2+2-3=0有解.(11分)
∴假设成立,即在x轴上存在点C,使得|CA|2+|CB|2=|AB|2成立.(12分)
10.(本小题满分12分)(2015广西南宁第二次适应性测试,文21,圆锥曲线中的存在、探索性问题,解答题)已知抛物线C:y=2x2,直线l:y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴的垂线交C于点N.
(1)证明:抛物线C在点N处的切线与AB平行;
(2)是否存在实数k使以AB为直径的圆M经过点N?若存在,求k的值;若不存在,请说明理由.
解:(1)证明:设A(x1,y1),B(x2,y2),
把y=kx+2代入y=2x2,
得2x2-kx-2=0,则x1+x2=k2.(1分)
∵xN=xM=x1+x22=k4,
∴N点的坐标为k4,k28.(2分)
∵y'=4x,∴y'|x=k4=k,(3分)
即抛物线在点N处的切线的斜率为k.(4分)
∵直线l:y=kx+2的斜率为k,∴l∥AB.(5分)
(2)假设存在实数k使以AB为直径的圆M经过点N.
∵M是AB的中点,∴|MN|=12|AB|.(6分)
由(1)知yM=12(y1+y2)=12(kx1+2+kx2+2)
=12[k(x1+x2)+4]=12k22+4=k24+2.(7分)
∵MN⊥x轴,
∴|MN|=|yM-yN|=k24+2-k28=k2+168.(8分)
|AB|=1+k2·(x1+x2)2-4x1x2(9分)
=1+k2·k22-4×(-1)
=12k2+1·k2+16.(10分)
∵k2+168=14k2+1·k2+16,∴k=±2.
存在实数k=±2使以AB为直径的圆M经过点N.(12分)
11.(本小题满分12分)(2015河南郑州第二次质量检测,文20,圆锥曲线中的存在、探索性问题,解答题)设椭圆C:x2a2+y2b2=1(a>b>0),F1,F2为左、右焦点,B为短轴端点,且S△BF1F2=4,离心率为22,O为坐标原点.
(1)求椭圆C的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点M,N,且满足|OM+ON|=|OM-ON|?若存在,求出该圆的方程;若不存在,请说明理由.
解:(1)由题意得S△BF1F2=12×2c×b=4,e=ca=22,a2=b2+c2,
解得a2=8,b2=4,所以椭圆C的方程为x28+y24=1.(4分)
(2)假设存在圆心在原点的圆x2+y2=r2,使得该圆的任意一条切线与椭圆C恒有两个交点M,N,
因为|OM+ON|=|OM-ON|,所以OM·ON=0.
设M(x1,y1),N(x2,y2),
当切线斜率存在时,设该圆的切线方程为y=kx+m,
联立y=kx+m,x28+y24=1,消去y得x2+2(kx+m)2=8,
即(1+2k2)x2+4kmx+2m2-8=0,(6分)
则Δ=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,即8k2-m2+4>0.
所以x1+x2=-4km1+2k2,x1x2=2m2-81+2k2,
y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2
=k2(2m2-8)1+2k2-4k2m21+2k2+m2=m2-8k21+2k2,
要使OM·ON=0,只需x1x2+y1y2=0,
即2m2-81+2k2+m2-8k21+2k2=0,所以3m2-8k2-8=0.
所以k2=3m2-88≥0.
又8k2-m2+4>0,所以m2>2,3m2≥8.
所以m2≥83,即m≥263或m≤-263.
因为直线y=kx+m为圆的一条切线,
所以圆的半径为r=|m|1+k2,
r2=m21+k2=m21+3m2-88=83,r=263,
所求圆的方程为x2+y2=83,(10分)
此时圆的切线y=kx+m都满足m≥263或m≤-263.
当切线的斜率不存在时,切线为x=±263,与椭圆x28+y24=1的两个交点为263,±263,-263,±263,满足OM·ON=0,此时圆的方程为x2+y2=83.
综上所述,存在圆心在原点的圆x2+y2=83满足条件.(12分)
12.(本小题满分12分)(2015辽宁东北育才学校五模,文20,圆锥曲线中的存在、探索性问题,解答题)已知椭圆的焦点坐标是F1(-1,0),F2(1,0),过点F2垂直于长轴的直线交椭圆于P,Q两点,且|PQ|=3.
(1)求椭圆的方程;
(2)求F2的直线与椭圆交于不同的两点M,N,则△F1MN的内切圆面积是否存在最大值?若存在,则求出这个最大值及此时的直线方程;若不存在,请说明理由.
解:(1)设椭圆的方程是x2a2+y2b2=1(a>b>0),
由焦点的坐标可知c=1,由|PQ|=3可得2b2a=3.
又因为a2-b2=c2,解得a=2,b=3,
故椭圆的方程为x24+y23=1.(4分)
(2)设M(x1,y1),N(x2,y2),不妨设y1>0,y2<0.
设△F1MN的内切圆半径是R,则△F1MN的周长是4a=8,S△F1MN=12(MN+F1M+F1N)R=4R,
因此S△F1MN最大,R就最大.
S△F1MN=12F1F2(y1-y2)=y1-y2.
由题知,直线l的斜率不为0,
可设直线l的方程为x=my+1,
由x=my+1,x24+y23=1得(3m2+4)y2+6my-9=0,
解得y1=-3m+6m2+13m2+4,
y2=-3m-6m2+13m2+4,
则S△F1MN=y1-y2=12m2+13m2+4.
令t=m2+1,则t≥1,
则S△F1MN=y1-y2=12m2+13m2+4=123t+1t.
令f(t)=3t+1t,f'(t)=3-1t2.
当t≥1时,f'(t)≥0,f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,S△F1MN≤124=3,
当且仅当t=1,m=0时,S△F1MN取到最大值3,
又S△F1MN=4R,所以Rmax=34,
此时所求内切圆面积的最大值是9π16.
故直线l:x=1,△F1MN的内切圆的面积最大值是9π16.(12分)
14.(本小题满分12分)(2015广西桂林、防城港一联,文20,圆锥曲线中的存在、探索性问题,解答题)已知圆C1:(x+2)2+y2=8116,圆C2:(x-2)2+y2=116,动圆Q与圆C1、圆C2均外切.
(1)求动圆圆心Q的轨迹方程;
(2)在x轴负半轴上是否存在定点M使得∠QC2M=2∠QMC2?若存在,求出点M的坐标;若不存在,请说明理由.
解:(1)圆C1的圆心C1(-2,0),半径R1=94.(1分)
圆C2的圆心C2(2,0),半径R2=14.
设动圆Q半径为r,
则|QC1|=94+r,|QC2|=14+r.(3分)
∴|QC1|-|QC2|=2.(4分)
∴点Q的轨迹是以C1(-2,0),C2(2,0)为焦点,实轴长为2的双曲线右支.
∴动圆圆心Q的轨迹方程是x2-y23=1(x≥1).(6分)
(2)假设点M存在,设M(t,0),Q(x0,y0)(x0≥1),
当x0≠2时,tan∠QC2M=-kQC2=-y0x0-2,
tan∠QMC2=kQM=y0x0-t.(7分)
∵∠QC2M=2∠QMC2,
∴-y0x0-2=2×y0x0-t1-y0x0-t2将y02=3x02-3代入并整理得(4+4t)x0=t2+4t+3.(9分)
∵Q(x0,y0)不唯一,
故4+4t=0,t2+4t+3=0,解得t=-1.(10分)
当x0=2时,∠QC2M=90°,而t=-1时,∠QMC2=45°,满足∠QC2M=2∠QMC2.(11分)
故满足条件的点M(-1,0)存在.(12分)
15.(本小题满分12分)(2015广西柳州3月模拟,文21,圆锥曲线中的存在、探索性问题,解答题)已知椭圆x2a2+y2b2=1(a>b>0)的一个焦点为F(2,0),且离心率为63.
(1)求椭圆的方程;
(2)斜率为k的直线l过点F,且与椭圆交于A,B两点,P为直线x=3上的一点,若△ABP为等边三角形,求直线l的方程.
解:(1)依题意有c=2,ca=63,可得a2=6,b2=2.
所以所求椭圆的方程为x26+y22=1.(4分)
(2)直线l的方程为y=k(x-2).
联立方程组y=k(x-2),x26+y22=1消去y并整理得
(3k2+1)x2-12k2x+12k2-6=0.
设A(x1,y1),B(x2,y2),
得x1+x2=12k23k2+1,x1x2=12k2-63k2+1,
所以|AB|=1+k2|x1-x2|=26(k2+1)3k2+1.
设AB的中点M(x0,y0),
得x0=6k23k2+1,y0=-2k3k2+1.
得直线MP的斜率为-1k,又xP=3,
所以|MP|=1+1k2·|x0-xP|=k2+1k2·3(k2+1)3k2+1.
当△ABP为正三角形时,|MP|=32|AB|,
即k2+1k2·3(k2+1)3k2+1=32·26(k2+1)3k2+1,
解得k=±1.
即直线l的方程为x-y-2=0或x+y-2=0.(12分)
16.(本小题满分12分)(2015吉林省吉林市二调,文21,圆锥曲线中的存在、探索性问题,解答题)设椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于Q点,且2F1F2+F2Q=0.
(1)求椭圆C的离心率;
(2)若过A,Q,F2三点的圆恰好与直线x-3y-3=0相切,求椭圆C的方程;
(3)过F2的直线l与(2)中椭圆交于不同的两点M,N,则△F1MN的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
解:(1)由题知A(0,b),设F1(-c,0),F2(c,0),则Q(-3c,0).
AQ=(-3c,-b),AF2=(c,-b),
由题知AQ⊥AF2,所以AQ·AF2=-3c2+b2=0,
所以b2=3c2,所以a2=4c2,
所以e=ca=12.(3分)
(2)Rt△QAF2外接圆的圆心为斜边QF2的中点F1(-c,0),所以r=2c.
因为Rt△QAF2的外接圆与直线x-3y-3=0相切,所以d=|-c-3|2=2c,所以c=1.
a=2c=2,b=3,故所求的椭圆方程为x24+y23=1.(6分)
(3)设M(x1,y1),N(x2,y2),由题易知y1,y2异号.
设△F1MN的内切圆的半径为R,
则△F1MN的周长为4a=8,
S△F1MN=12(|MN|+|F1M|+|F1N|)R=4R,
因此要使△F1MN内切圆的面积最大,只需R最大.
S△F1MN=12|F1F2||y1-y2|=|y1-y2|.(7分)
由题意知直线l的斜率不为零,可设直线l的方程x=my+1.
由x=my+1,x24+y23=1得(3m2+4)y2+6my-9=0.
Δ>0⇒m∈R.
由韦达定理得y1+y2=-6m3m2+4,y1y2=-93m2+4.(9分)
S△F1MN=|y1-y2|=12m2+13m2+4,
令t=m2+1(t≥1).(10分)
S△F1MN=12t3t2+1=123t+1t(t≥1),
当t=1时,S△F1MN有最大值3,即4R=3,此时m=0,Rmax=34.
故△F1MN的内切圆的面积最大值为9π16,此时直线l的方程为x=1.(12分)