中考复习数学专题张海群

中考复习数学专题张海群

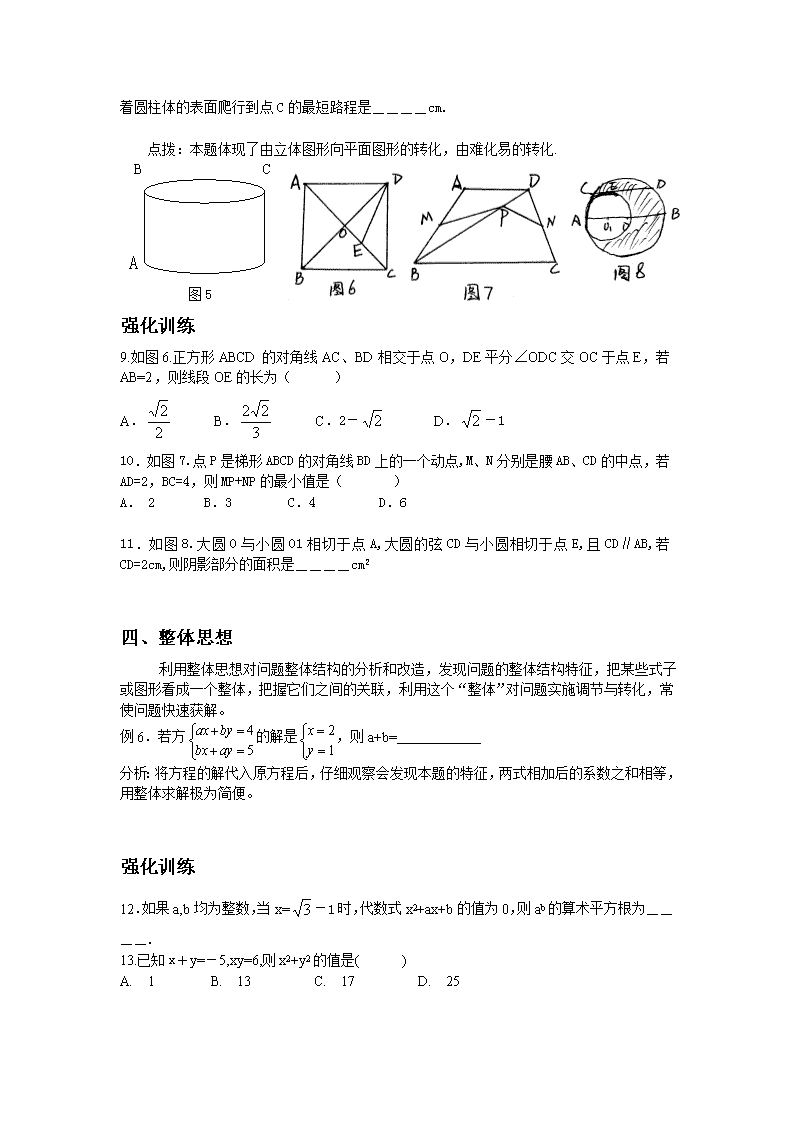
中考数学专题复习 ------数学思想方法 ‎ 江州区江州二中 张海群 ‎【简要分析】‎ ‎ 中考命题遵循着两条线:一条是明线,以选择题、填空题、解答题等外在形式考查数、式、方程、函数、四边形、圆等初中数学的重要内容；一条是暗线，通过试题重点考查初中数学常用思想方法。数学思想方法是数学的生命和灵魂，是数学知识的精髓，是把知识转化成能力的桥梁，对数学方法掌握得如何直接影响着整个解题思路。随着中考改革的深入，中考试题从知识型转化到能力型，更注重了对数学思想方法的考查。‎ ‎ 初中阶段的数学思想方法主要有：数形结合思想、分类讨论思想、转化思想、整体思想、方程思想、函数思想等.‎ ‎【典型例子分析】‎ 一、数形结合思想 数形结合是解决数学问题的最重要的思想方法之一，是根据数学问题的题设和结论之间的内在联系，既分析其数量关系，又揭示其几何意义，使数量关系和几何图形巧妙地结合起来，并利用这种结合，探索解决问题的思路。应用其解决问题可使问题更形象直观.‎ 例1．如图1.已知函数y=x+b和y=ax+3的图象的交点为P,则不等式x+b﹥ax+3的解 集为＿＿＿＿‎ ‎ y=x+b 例2．二次函数y=ax2+bx+c(a≠0)的图象如图2,根据图象解答下列问题; ‎ ‎（1）写出方程ax2+bx+c=0的两个根； 0 1‎ ‎（2）写出不等式ax2+bx+c﹥0的解集； y=ax+3‎ ‎（3）写出y随x的增大而减小的自变量x的取值范围； 图1‎ ‎（4）若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围。‎ 强化训练 ‎1．实数a,b在数轴上的位置如图3,下列各式正确的是( ) a o b A.a＞0 B.b＜0 C.a－b＞0 D. b－a＞0 图3‎ ‎2．反比例函数y＝ 的图象如图4，点M是该函数图象上 的一点，MN垂直于x轴，垂足是点N，如果△MON的面积是2，‎ 则k的值为（ ）‎ A．2 B．－2 C．4 D．－4‎ 二、分类讨论思想 ‎ 分类是按照数学对象的相同点和差异点，将数学对象分为不同种类的思想方法，其目的是复杂问题简单化。‎ 例3．已知关于的方程(a2－1)x2+2(a+2)x+1=0有实数根，求a的取值范围。 ‎ ‎ 分析：题中未指明关于x的方程是一次方程还是二次方程，所以要分(a2－1)=0与(a2－1) ≠0两种情况讨论，即方程的次数进行分类。‎ 例4．在平面直角坐标系中,O为坐标原点,二次函数y=－x2+(k－1)x+4的图象与y轴交于点A,与x轴的负半轴交于点B,且△OAB 的面积是6.‎ (1) 求点A与点B的坐标;‎ (2) 求此二次函数的解析式;‎ (3) 如果点P在x轴上,且△ABP是等腰三角形,求点P的坐标 分析：前两问容易解答，第（3）问已知两个点确定第三个点，使这三个点构成的三角形为等腰三角形的问题，由于未说明哪两条边为腰，从而要分类讨论，要做到不重不漏，确定好分类方向.‎ 强化训练 ‎3.若等腰梯形的三边长分别是3,4,11,则这个等腰梯形的周长为( )‎ A. 21 B. 29 C. 21或29 D. 21或22或29‎ ‎4.圆中的两条弦AB,CD,且AB∥CD,AB=12,CD=16,圆的半径为10,则弦AB与CD的距离为＿＿＿＿＿＿＿.‎ ‎5.若直角三角形的两边长为3,4,第三边长为＿＿＿＿.‎ ‎6.若直线y=－4x＋b与两坐标轴围成的三角形的面积是5,则b的值为( )‎ A. ±2 B. ±2 C. 2 D.－2‎ ‎7.一组数据5，7，7，x的中位数与平均数相等，则x的值为＿＿＿.‎ ‎8.已知⊙O和⊙A相切于点P，半径分别为1和3，⊙O和⊙A的圆心距是＿＿＿＿.‎ 三、转化思想 ‎ 利用转化思想解题的过程就是把所要解决的问题转化为已知熟悉的问题的过程，通过条件的转化，结论的转化，化难为易，化繁为简，最终使问题得以解决.常见的转化有:已知与未知的转化,特殊与一般的转化,动与静的转化,抽象与具体的转化.‎ 例5．如图5.一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是＿＿＿＿cm.‎ 点拨：本题体现了由立体图形向平面图形的转化，由难化易的转化.‎ ‎ B C ‎ ‎ 图5 ‎ A ‎ ‎ 图5‎ 强化训练 ‎9.如图6.正方形ABCD的对角线AC、BD相交于点O，DE平分∠ODC交OC于点E，若AB=2，则线段OE的长为（ ）‎ A． B． C．2－ D．－1 ‎ ‎10．如图7.点P是梯形ABCD的对角线BD上的一个动点,M、N分别是腰AB、CD的中点，若AD=2，BC=4，则MP+NP的最小值是（ ）‎ A． 2 B．3 C．4 D．6‎ ‎11．如图8.大圆O与小圆O1相切于点A,大圆的弦CD与小圆相切于点E,且CD∥AB,若CD=2cm,则阴影部分的面积是＿＿＿＿cm2‎ 四、整体思想 ‎ 利用整体思想对问题整体结构的分析和改造，发现问题的整体结构特征，把某些式子或图形看成一个整体，把握它们之间的关联，利用这个“整体”对问题实施调节与转化，常使问题快速获解。‎ 例6．若方的解是，则a+b= ‎ 分析：将方程的解代入原方程后，仔细观察会发现本题的特征，两式相加后的系数之和相等，用整体求解极为简便。‎ 强化训练 ‎12．如果a,b均为整数，当x=－1时，代数式x2+ax+b的值为0，则ab的算术平方根为＿＿＿＿.‎ ‎13.已知x＋y=－5,xy=6,则x2+y2的值是( )‎ A. 1 B. 13 C. 17 D. 25‎ ‎14.已知x2+x－1=0,2x3+4x2+3的值为＿＿＿＿.‎ 五、方程思想 ‎ 方程思想是对所求问题通过列方程求解的一种思维方法,是解几何计算题的重要策略.‎ 例7.如图9.矩形纸片ABCD，AB=8，BC=12，点M在BC边上，且CM=4，将矩形纸片折叠使点D落在点M处，折痕为EF，则AE的长为＿＿＿＿.‎ 点拨:求线段的长常用到方程思想其中常用勾股定理、‎ 相似构造关于线段的方程。‎ 强化训练 ‎ ‎15．如图10.是某宾馆大厅到二楼的楼梯设计图,已知BC=6米,AB=9米,中间平台宽度DE为2米,DM,EN为平台的两根支柱,DM,EN垂直于AB,垂足分别为M,N,∠EAB=300, ∠CDF=450.求DM和BC的水平距离BM.(精确到0.1米,参考数据: ≈1.41,≈1.73)‎ 六、函数思想 ‎ 理解实际问题中数量关系,构造函数模型,‎ 应用函数知识解决问题.‎ 例8.如图11.已知一抛物线形大门,其地面宽度AB=18m,一同学站在门内,在离门脚B点1m远的D处,垂直地面立起一根1.7m长的杆,其顶端恰好顶在抛物线形门上C处,根据这些条件,请你求出该大门的高h.‎ ‎ 分析：选择恰当的位置建立平面直角坐标系，用待定系数法确定抛物线解析式，进而利用二次函数的性质解决问题。‎ 强化训练 ‎ ‎16．“三农”优惠政策，使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元每千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元每千克)有如下关系:w=－2x+80.设这种产品每天的销售利润为y(元).‎ ‎(1)求y与x之间的函数关系式;‎ ‎(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?‎ ‎(3)如果物价部门规定这种产品的销售价不得高于28元每千克,若该农户想要每天的销售利润最大,销售价应定为多少元? 最大利润是多少?若该农户想要每天获得150元的销售利润,‎ ‎ 销售价应定为多少元?‎ 附参考答案 典型例子答案 例1: x﹥1‎ ‎ 例2： (1) x1=1,x2=3; (2)1＜x＜3; (3)x＞2 (4)k＜2.‎ ‎ 例3：a≥－‎ ‎ 例4：解：（1）点A的坐标为（0，4），点B的坐标为（－3，0）‎ ‎ （2）二次函数的解析式为y=－x2－x+4‎ ‎ (3)因为△ABP是等腰三角形，所以 ‎ 当AB=AP时，点P的坐标为（3，0）‎ ‎ 当AB=BP时，点P的坐标为（2，0）或（－8，0）‎ ‎ 当AP=BP时，点P的坐标为（，0）‎ ‎ 综上所述：点P的坐标为（3，0），（2，0），（－8，0），（，0）。‎ 例5： 13‎ 例6： 3‎ 例7： 2 （提示：过点E作EH垂直BC于点H，利用△EHM∽△MCF可得。）‎ 例8： 8.1米 强化训练 ‎1.D 2.D 3.B 4. 2或14 5. 5或 6.B 7. 5或9‎ ‎8. 2或4 9.C 10.B 11. 12. 13.B ‎14. 5 15. 4.6米 ‎16.(1)y=(x－20)w=(x－20)( －2x+80)= －2x2+120x－1600‎ ‎ (2)y=－2x2+120x－1600=－2(x－30)2+200‎ ‎ ∴当销售价定为30元／千克时,每天的销售利润最大，最大利润是200元.‎ ‎ (3) y=－2(x－30)2+200‎ ‎ ∵a=－2,抛物线的开口方向向下，对称轴是x=30‎ ‎ ∴x＜30时,y随x的增大而增大 ‎ ∵物价部门规定这种产品的销售价不得高于28元每千克 ‎ ∴销售价定为28元每千克时，每天的销售利润最大。‎ ‎ 最大利润是192元 ‎ 当y=150时，－2(x－30)2+200=150.‎ 解得:x1=25,x2=35 ‎ 依题意, x2=35＞28不符合题意,应舍去. ‎ ‎ 该农户想要每天获得150元的销售利润, 销售价应定为25元每千克