2016年普通高等学校招生全国统一考试(四川卷)数学(文史类)

2016年普通高等学校招生全国统一考试(四川卷)数学(文史类)

‎2016年普通高等学校招生全国统一考试(四川卷)‎ 数学(文史类)‎ ‎1.(2016四川,文1)设i为虚数单位,则复数(1+i)2=(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A.0 B.2 C.2i D.2+2i 答案C　由题意,(1+i)2=1+2i+i2=2i　,故选C.‎ ‎2.(2016四川,文2)设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是(　　)‎ A.6 B.5 C.4 D.3‎ 答案B　由题意,A∩Z={1,2,3,4,5}　,故其中的元素个数为5,选B.‎ ‎3.(2016四川,文3)抛物线y2=4x的焦点坐标是(　　)‎ A.(0,2) B.(0,1)‎ C.(2,0) D.(1,0)‎ 答案D　由题意,y2=4x的焦点坐标　为(1,0),故选D.‎ ‎4.(2016四川,文4)为了得到函数y=sinx+‎π‎3‎的图象,只需把函数y=sin x的图象上所有的点(　　)‎ A.向左平行移动π‎3‎个单位长度 B.向右平行移动π‎3‎个单位长度 C.向上平行移动π‎3‎个单位长度 D.向下平行移动π‎3‎个单位长度 答案A　由题意,为得到函数y=sinx+‎π‎3‎,只需把函数y=sin x的图象上所有点向左平行移动　π‎3‎个单位长度,故选A.‎ ‎5.(2016四川,文5)设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的(　　)‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 答案A　由题意,x>1且y>1,则x+y>2,而当x+y>2　‎ 时不能得出x>1且y>1　.故p是q的充分不必要条件,选A.‎ ‎6.(2016四川,文6)已知a为函数f(x)=x3-12x的极小值点,则a=(　　)‎ A.-4 B.-2 C.4 D.2‎ 答案D　f'(x)=3x2-12=3(x+2)(x-2),令f'(x)=0,得x=-2或x=2,‎ 易得f(x)在(-2,2)上单调递减,在(-∞,-2),(2,+∞)　‎ 上单调递增　,‎ 故f(x)极小值为f(2),由已知得a=2,故选D.‎ ‎7.(2016四川,文7)某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(　　)‎ ‎(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)‎ A.2018年 B.2019年 C.2020年 D.2021年 答案B　设从2015年后第n年该公司全年投入的研发资金开始超过200万元,‎ 由已知得130×(1+12%)n>200,∴1.12n>‎200‎‎130‎.　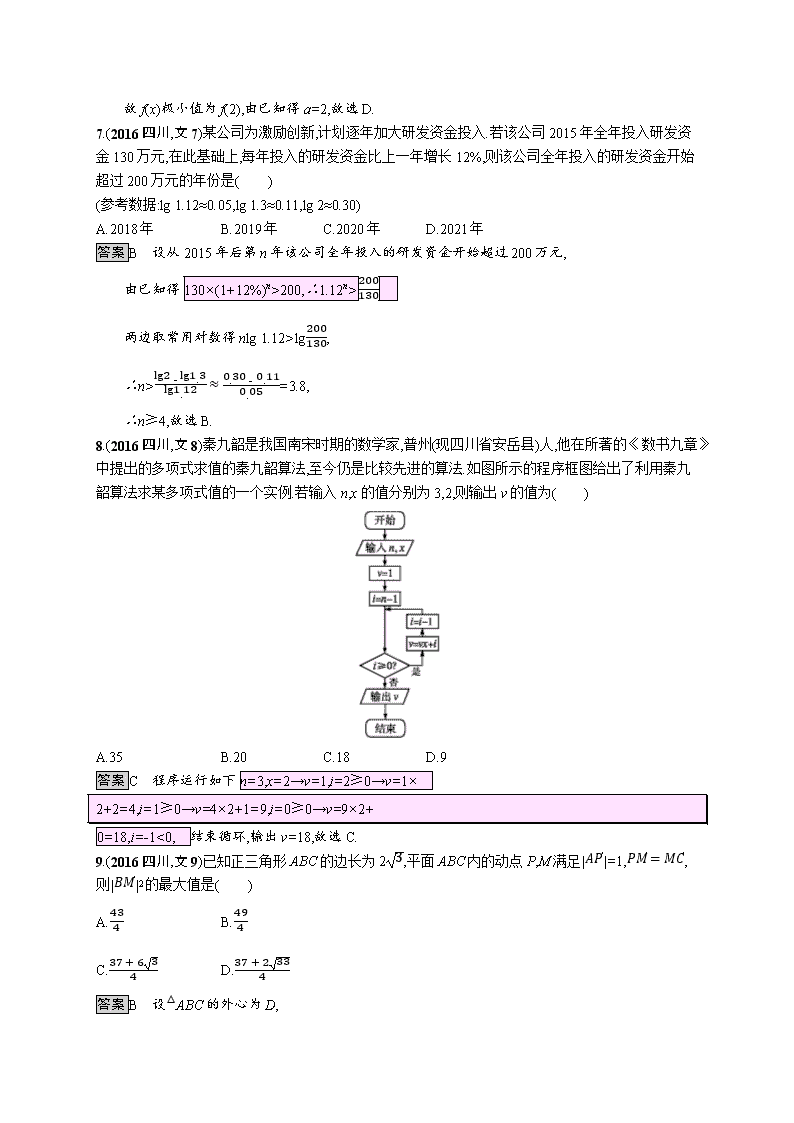‎ 两边取常用对数得nlg 1.12>lg‎200‎‎130‎,‎ ‎∴n>lg2-lg1.3‎lg1.12‎‎≈‎‎0.30-0.11‎‎0.05‎=3.8,‎ ‎∴n≥4,故选B.‎ ‎8.(2016四川,文8)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为3,2,则输出v的值为(　　)‎ A.35 B.20 C.18 D.9‎ 答案C　程序运行如下n=3,x=2→v=1,i=2≥0→v=1×　‎ ‎2+2=4,i=1≥0→v=4×2+1=9,i=0≥0→v=9×2+　‎ ‎0=18,i=-1<0,　结束循环,输出v=18,故选C.‎ ‎9.(2016四川,文9)已知正三角形ABC的边长为2‎3‎,平面ABC内的动点P,M满足|AP|=1,PM‎=‎MC,则|BM|2的最大值是(　　)‎ A.‎43‎‎4‎ B.‎‎49‎‎4‎ C.‎37+6‎‎3‎‎4‎ D.‎‎37+2‎‎33‎‎4‎ 答案B　设△ABC的外心为D,‎ 则|DA|=|DB|=|DC|=2.‎ 以D为原点,直线DA为x轴,过D点的DA的垂线　‎ 为y轴,建立平面直角坐标系,　‎ 则A(2,0),B(-1,-‎3‎),C(-1,‎3‎).‎ 设P(x,y),由已知|AP|=1,得(x-2)2+y2=1,‎ ‎∵PM‎=‎MC,∴Mx-1‎‎2‎‎,‎y+‎‎3‎‎2‎.‎ ‎∴BM‎=‎x+1‎‎2‎‎,‎y+3‎‎3‎‎2‎.‎ ‎∴BM‎2‎‎=‎‎(x+1‎)‎‎2‎+(y+3‎‎3‎‎)‎‎2‎‎4‎,它表示圆(x-2)2+y2=1上点(x,y)与点(-1,-3‎3‎)距离平方的‎1‎‎4‎,‎ ‎∴(|BM|2)max=‎1‎‎4‎‎(‎‎3‎‎2‎‎+(0+3‎‎3‎‎)‎‎2‎+1)2=‎49‎‎4‎,故选B.‎ ‎10.(2016四川,文10)设直线l1,l2分别是函数f(x)=‎-lnx,01‎图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是(　　)‎ A.(0,1) B.(0,2)‎ C.(0,+∞) D.(1,+∞)‎ 答案A　由题意得P1,P2分别位于两段函数的图象上.　‎ 设P1(x1,ln x1),P2(x2,-ln x2)(不妨设x1>1,01,∴S△PAB=‎1‎‎2‎|yA-yB|·|xP|=‎2‎x‎1‎‎1+‎x‎1‎‎2‎‎<‎‎1+‎x‎1‎‎2‎‎1+‎x‎1‎‎2‎=1.‎ ‎∴00.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.‎ 由0.50×(x-2)=0.5-0.48,解得x=2.04.‎ 故可估计居民月均用水量的中位数为2.04吨.‎ ‎17.‎ ‎(2016四川,文17)如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=‎1‎‎2‎AD.‎ ‎(1)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;‎ ‎(2)证明:平面PAB⊥平面PBD.‎ 解(1)取棱AD的中点M(M∈平面PAD),点M即为所求的一个点.理由如下:‎ 因为AD∥BC,BC=‎1‎‎2‎AD,‎ 所以BC∥AM,且BC=AM.‎ 所以四边形AMCB是平行四边形,从而CM∥AB.‎ 又AB⊂平面PAB,CM⊄平面PAB,　‎ 所以CM∥平面PAB.　‎ ‎(说明:取棱PD的中点N,则所找的点可以是直线MN上任意一点)‎ ‎(2)由已知,PA⊥AB,PA⊥CD,‎ 因为AD∥BC,BC=‎1‎‎2‎AD,‎ 所以直线AB与CD相交.‎ 所以PA⊥平面ABCD.从而PA⊥BD.‎ 因为AD∥BC,BC=‎1‎‎2‎AD,‎ 所以BC∥MD,且BC=MD.‎ 所以四边形BCDM是平行四边形.‎ 所以BM=CD=‎1‎‎2‎AD,所以BD⊥AB.‎ 又AB∩AP=A,　所以BD⊥平面PAB.‎ 又BD⊂平面PBD,所以平面PAB⊥平面PBD.‎ ‎18.(2016四川,文18)在△ABC中,角A,B,C所对的边分别是a,b,c,且cosAa‎+cosBb=‎sinCc.‎ ‎(1)证明:sin Asin B=sin C;‎ ‎(2)若b2+c2-a2=‎6‎‎5‎bc,求tan B.‎ 解(1)根据正弦定理,可设asinA‎=bsinB=‎csinC=k　(k>0).‎ 则a=ksin A,b=ksin B,c=ksin C.‎ 代入cosAa‎+cosBb=‎sinCc中,有cosAksinA‎+cosBksinB=‎sinCksinC,‎ 变形可得sin Asin B=sin Acos B+cos Asin B=　‎ sin(A+B).　‎ 在△ABC中,由A+B+C=π,有sin(A+B)=sin(π-C)=sin C,所以sin Asin B=sin C.‎ ‎(2)由已知,b2+c2-a2=‎6‎‎5‎bc,‎ 根据余弦定理,有cos A=b‎2‎‎+c‎2‎-‎a‎2‎‎2bc‎=‎‎3‎‎5‎.‎ 所以sin A=‎1-cos‎2‎A‎=‎‎4‎‎5‎.‎ 由(1),sin Asin B=sin Acos B+cos Asin B,‎ 所以‎4‎‎5‎sin B=‎4‎‎5‎cos B+‎3‎‎5‎sin B,‎ 故tan B=sinBcosB=4.‎ ‎19.(2016四川,文19)已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N*.‎ ‎(1)若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;‎ ‎(2)设双曲线x2-y‎2‎an‎2‎=1的离心率为en,且e2=2,求e‎1‎‎2‎‎+‎e‎2‎‎2‎+…+en‎2‎.‎ 解(1)由已知,Sn+1=qSn+1,Sn+2=qSn+1+1,　‎ 两式相减得到an+2=qan+1,n≥1.　‎ 又由S2=qS1+1得到a2=qa1,‎ 故an+1=qan对所有n≥1都成立.‎ 所以,数列{an}是首项为1,公比为q的等比数列.‎ 从而an=qn-1.‎ 由a2,a3,a2+a3成等差数列,可得2a3=a2+a2+a3.‎ 所以a3=2a2,故q=2.‎ 所以an=2n-1(n∈N*).‎ ‎(2)由(1)可知,an=qn-1.‎ 所以双曲线x2-y‎2‎an‎2‎=1的离心率en=‎1+‎an‎2‎‎=‎‎1+‎q‎2(n-1)‎.‎ 由e2=‎1+‎q‎2‎=2,解得q=‎3‎.‎ 所以e‎1‎‎2‎‎+‎e‎2‎‎2‎+…+‎en‎2‎ ‎=(1+1)+(1+q2)+…+[1+q2(n-1)]‎ ‎=n+[1+q2+…+q2(n-1)]‎ ‎=n+q‎2n-1‎q‎2‎‎-1‎=n+‎1‎‎2‎(3n-1).‎ ‎20.(2016四川,文20)已知椭圆E:x‎2‎a‎2‎‎+‎y‎2‎b‎2‎=1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P‎3‎‎,‎‎1‎‎2‎在椭圆E上.‎ ‎(1)求椭圆E的方程;‎ ‎(2)设不过原点O且斜率为‎1‎‎2‎的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.‎ 解(1)由已知,a=2b.‎ 又椭圆x‎2‎a‎2‎‎+‎y‎2‎b‎2‎=1(a>b>0)过点P‎3‎‎,‎‎1‎‎2‎,‎ 故‎3‎‎4‎b‎2‎‎+‎‎1‎‎4‎b‎2‎=1,解得b2=1.‎ 所以椭圆E的方程是x‎2‎‎4‎+y2=1.‎ ‎(2)设直线l的方程为y=‎1‎‎2‎x+m(m≠0),A(x1,y1),B(x2,y2),‎ 由方程组x‎2‎‎4‎‎+y‎2‎=1,‎y=‎1‎‎2‎x+m,‎得x2+2mx+2m2-2=0,①‎ 方程①的判别式为Δ=4(2-m2).‎ 由Δ>0,即2-m2>0,解得-‎2‎1时,g(x)>0;‎ ‎(3)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.‎ 解(1)f'(x)=2ax-‎1‎x‎=‎‎2ax‎2‎-1‎x(x>0).‎ 当a≤0时,f'(x)<0,f(x)在(0,+∞)内单调递减.‎ 当a>0时,由f'(x)=0有x=‎1‎‎2a.‎ 当x∈‎0,‎‎1‎‎2a时,f'(x)<0,f(x)单调递减;　‎ 当x∈‎1‎‎2a‎,+∞‎时,f'(x)>0,f(x)单调递增.　‎ ‎(2)令s(x)=ex-1-x,则s'(x)=ex-1-1.‎ 当x>1时,s'(x)>0,所以ex-1>x,从而g(x)=‎1‎x‎-‎‎1‎ex-1‎>0.‎ ‎(3)由(2),当x>1时,g(x)>0.‎ 当a≤0,x>1时,f(x)=a(x2-1)-ln x<0.‎ 故当f(x)>g(x)在区间(1,+∞)内恒成立时,必有a>0.　‎ 当01.‎ 由(1)有f‎1‎‎2a0,‎ 所以此时f(x)>g(x)在区间(1,+∞)内不恒成立.‎ 当a≥‎1‎‎2‎时,令h(x)=f(x)-g(x)(x≥1).‎ 当x>1时,h'(x)=2ax-‎1‎x‎+‎‎1‎x‎2‎-e1-x>x-‎1‎x+　‎1‎x‎2‎‎-‎1‎x=x‎3‎‎-2x+1‎x‎2‎>‎x‎2‎‎-2x+1‎x‎2‎>0.　‎ 因此,h(x)在区间(1,+∞)单调递增.‎ 又因为h(1)=0,所以当x>1时,h(x)=f(x)-g(x)>0,即f(x)>g(x)恒成立.‎ 综上,a∈‎1‎‎2‎‎,+∞‎.‎