【数学】2020届一轮复习人教A版命题及其关系、充分条件与必要条件学案
第2讲 命题及其关系、充分条件与必要条件
1.了解命题的概念.
2.了解四种命题,会分析四种命题的相互关系.
3.理解必要条件、充分条件与充要条件的含义,能初步判断给定的两个命题的关系.
知识梳理
1.命题及其真假
(1)命题:在数学上,用 语言、符号或式子 表达的,可以判断 真假 的 陈述句 叫做命题.
(2)真命题:判断为真的语句叫做 真命题 .
(3)假命题:判断为假的语句叫做 假命题 .
2.四种命题的形式
(1)原命题:“若p,则q”,其中p为命题的条件,q为命题的结论.
(2)逆命题:“若q,则p”,即交换原命题的条件和结论.
(3)否命题:“若﹁p,则﹁q”,即同时否定原命题的条件和结论.
(4)逆否命题:“若﹁q,则﹁p”,即交换原命题的条件和结论后,再同时加以否定.
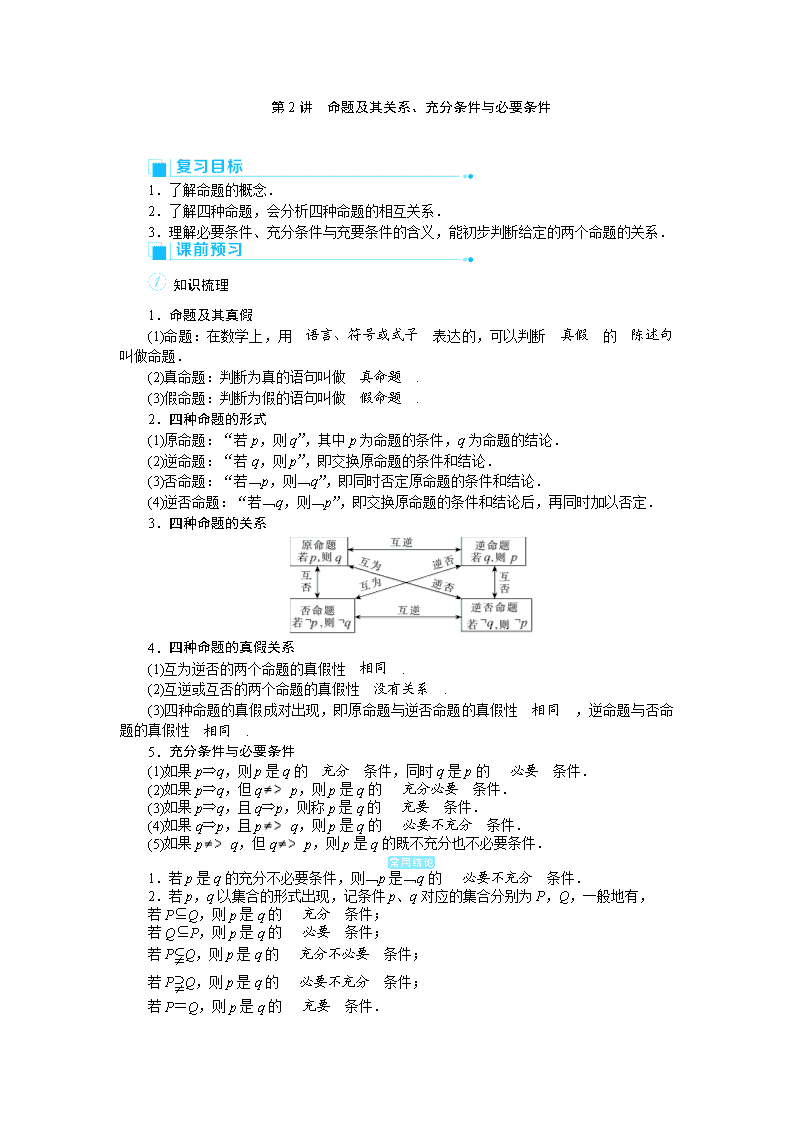
3.四种命题的关系
4.四种命题的真假关系
(1)互为逆否的两个命题的真假性 相同 .
(2)互逆或互否的两个命题的真假性 没有关系 .
(3)四种命题的真假成对出现,即原命题与逆否命题的真假性 相同 ,逆命题与否命题的真假性 相同 .
5.充分条件与必要条件
(1)如果p⇒q,则p是q的 充分 条件,同时q是p的 必要 条件.
(2)如果p⇒q,但q p,则p是q的 充分必要 条件.
(3)如果p⇒q,且q⇒p,则称p是q的 充要 条件.
(4)如果q⇒p,且p q,则p是q的 必要不充分 条件.
(5)如果p q,但q p,则p是q的既不充分也不必要条件.
1.若p是q的充分不必要条件,则﹁p是﹁q的 必要不充分 条件.
2.若p,q以集合的形式出现,记条件p、q对应的集合分别为P,Q,一般地有,
若P⊆Q,则p是q的 充分 条件;
若Q⊆P,则p是q的 必要 条件;
若PÜQ,则p是q的 充分不必要 条件;
若PÝQ,则p是q的 必要不充分 条件;
若P=Q,则p是q的 充要 条件.
热身练习
1.下列语句中,不能构成命题的是(C)
A.5>12 B.若=,则x=y
C.x>0 D.若x
0无法判断真假,因此不能构成命题.
2.设m∈R,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是(D)
A.若方程x2+x-m=0有实根,则m>0
B.若方程x2+x-m=0有实根,则m≤0
C.若方程x2+x-m=0没有实根,则m>0
D.若方程x2+x-m=0没有实根,则m≤0
根据逆否命题的定义,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是“若方程x2+x-m=0没有实根,则m≤0”.故选D.
3.已知命题p:若x=-1,则向量a=(1,x)与b=(x+2,x)共线,则在命题p的原命题,逆命题,否命题,逆否命题中,真命题的个数为(B)
A.0 B.2
C.3 D.4
原命题:若x=-1,向量a=(1,-1),b=(1,-1),a与b共线,所以原命题为真,故逆否命题也为真.
逆命题为:若向量a=(1,x)与b=(x+2,x)共线,则x=-1.当a与b共线时,x(x+2)=x,解得x=0或-1.所以逆命题为假命题,从而否命题也为假命题.
故真命题的个数为2.
4.(2016·四川卷)设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的(A)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
因为所以x+y>2,即p⇒q.
而当x=0,y=3时,有x+y=3>2,但不满足x>1且y>1,即qp.故p是q的充分不必要条件.
5.设p:x<3,q:-1<x<3,则p是q成立的(C)
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
根据充分、必要条件的定义直接利用数轴求解即可.
将p,q对应的集合在数轴上表示出来如图所示,
易知,当p成立时,q不一定成立;当q成立时,p一定成立,故p是q成立的必要不充分条件.
四种命题及其真假判断
原命题为“若z1,z2互为共轭复数,则|z1|=|z2|”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是
A.真,假,真 B.假,假,真
C.真,真,假 D.假,假,假
“若z1,z2互为共轭复数,则|z1|=|z2|”,由共轭复数的定义可知为真命题,所以逆否命题也为真命题,
逆命题为:“复数|z1|=|z2|,则z1,z2互为共轭复数”,
由1和i的模相等,但它不是共轭复数,可知逆命题为假命题,
所以否命题也为假命题.故选B.
B
(1)判断一个命题为真命题,要给出推理证明;判断一个命题是假命题,只需举出反例即可;
(2)四种命题的真假成对出现.即原命题与逆否命题的真假性相同,逆命题与否命题的真假性相同.当一个命题直接判断不易进行时,可转化判断其等价命题的真假.
1.在下列4个结论中:
①命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”;
②命题“若m2+n2=0,则m,n全为0”的否命题是“若m2+n2≠0,则m,n全不为0”;
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为真命题;
④“若x>1,则x2>1”的否命题为真命题.
其中正确结论的序号是 ①③ .
①正确.
②不正确,否命题为“若m2+n2≠0,则m,n不全为0”.
③m>0时,Δ=1+4m>0,所以原命题为真命题,所以逆否命题为真命题.
④逆命题“若x2>1,则x>1”为假命题,所以否命题为假命题.
故正确结论的序号为①③.
充要条件的判断
(1)(2017·天津卷)设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
(2)如果x,y是实数,那么“x≠y”是“cos x≠cos y”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(1)(方法一)因为2-x≥0⇔ x≤2.
因为|x-1|≤1⇔-1≤x-1≤1⇔0≤x≤2.
因为x≤2 0≤x≤2,而0≤x≤2⇒x≤2,
所以“2-x≥0”是“|x-1|≤1”的必要而不充分条件.
(方法二)记“2-x≥0”与“|x-1|≤1”表示的集合分别为A,B.
则A={x|x≤2},B={x|0≤x≤2}.
因为BÜA,
所以“2-x≥0”是“|x-1|≤1”的必要而不充分条件.
(2)x=y⇒cos x=cos y,而cos x=cos y x=y,
利用四种命题的等价关系得:
cos x≠cos y⇒x≠y,x≠y cos x≠cos y.
所以“x≠y”是“cos x≠cos y”必要而不充分条件.
(1)B (2)B
(1)判断充要条件的方法:
①定义法(这是基本方法);②集合法(根据p,q成立的对象的集合之间的包含关系进行判断);③转换法.
(2)判断充要条件时,要注意如下技巧:
①等价化简:先将条件和结论等价化简,然后根据定义进行判断;
②等价转化:根据“四种命题”中互为逆否的两个命题是等价的,把判断命题的正确性,转化为判断其逆否命题的正确性.这种方法特别适合以否定形式给出的命题.
2.(1)“x<0”是“ln(x+1)<0”的(B)
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(2)如果a,b是实数,那么“a≠0”是“ab≠0”的(B)
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(1)ln(x+1)<0⇔00),若﹁p是﹁q的必要不充分条件,则实数m的取值范围为____________.
p对应的集合为A={x|-2≤x≤10},q对应的集合为B={x|1-m≤x≤1+m},
因为﹁p是﹁q 的必要不充分条件,
所以﹁q⇒﹁p但﹁p﹁q
由互为逆否的两个命题的等价关系可知,
p⇒q,但qp,所以AÜB.
所以解得m≥9.
检验m=9时,满足AÜB.
因此,实数m的取值范围是[9,+∞).
[9,+∞)
(1)充分条件、必要条件或充要条件的应用,一般表现在参数问题的求解上,求解一般步骤为:
①首先要将p,q等价化简;
②将充分条件、必要条件或充要条件转化为集合之间的包含关系;
③列出关于参数的等式或不等式组,求出参数的值或取值范围.
(2)解此类问题要注意:
①注意命题等价转化,如将﹁p与﹁q的关系转化为p与q的关系;
②注意区间端点值的检验.
3.已知p:2x+m<0,q:x2-x-2>0,若p是q的一个充分不必要条件,则实数m的取值范围为 [2,+∞) .
因为q:x2-x-2>0,所以x<-1或x>2,
记A={x|x<-1或x>2}.
又因为p:2x+m<0,所以x<-,
记B={x|x<-},
因为p是q的充分不必要条件,所以BÜA.
所以-≤-1,解得m≥2.
所以实数m的取值范围是[2,+∞).
1.判断一个语句是否为命题,关键是看能否判断真假.数学中的定义、公理、定理都是命题,但命题与定理是有区别的:命题有真假之分,而定理都是真命题.
2.一个命题和它的逆否命题同真假,而与它的其他两个命题的真假无此规律,判断一个命题为真必须经过证明,而判定一个命题为假只需举一个反例就行.
3.判断充分条件和必要条件时,常用以下几种方法:
(1)定义法:判断A是B的什么条件,实际上就是判断AB或BA是否成立,只要把题目中所给条件按逻辑关系画出箭头示意图,再利用定义即可判断.
(2)转换法:当所给命题的充要条件不易判断时,可对命题进行等价转换,如利用其逆否命题进行判断.
(3)集合法:当条件和结论以集合形式出现时,可利用集合间的包含关系进行判断.