- 2021-04-27 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
泰勒展开式在高考题中的应用
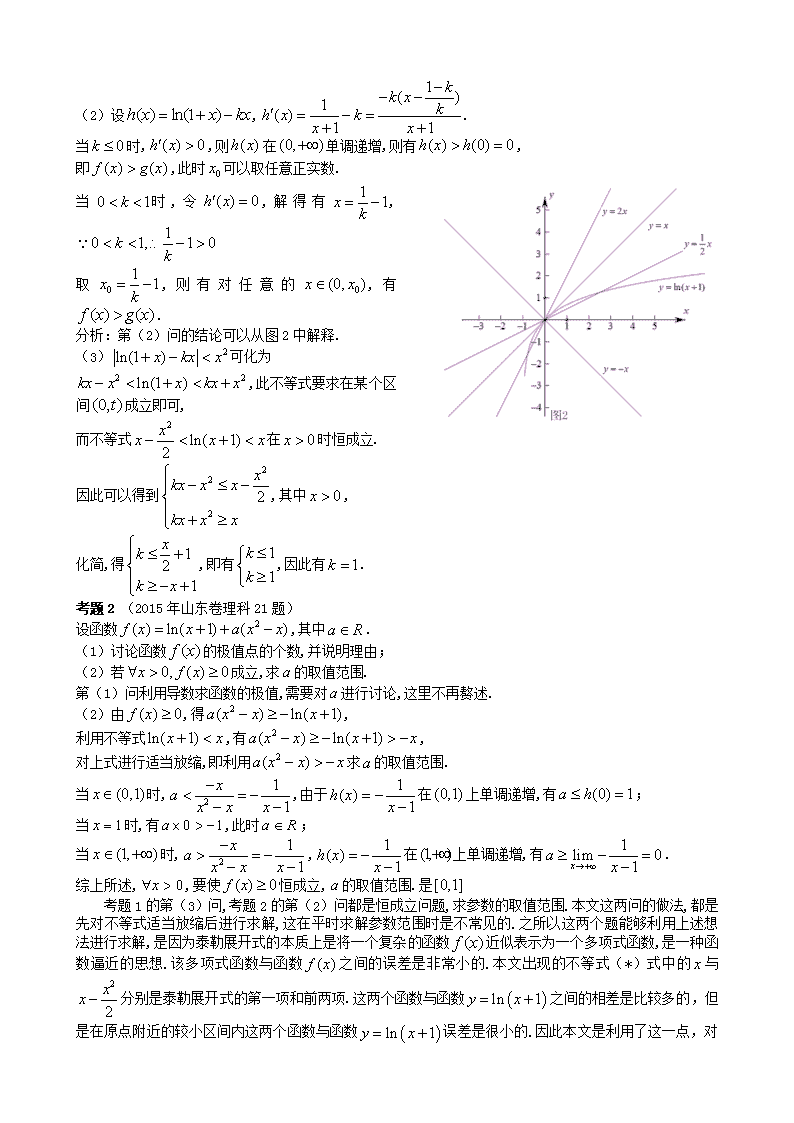
泰勒展开式在高考题中的应用 莲塘一中 李树森 高中数学中函数导数部分占据了重要的位置,高考试题中函数导数题往往也是以难题、压轴题形式出现.如何应对函数导数难题?高等数学中有一些知识、方法与中学数学相通,本文针对一类函数导数问题借助高等数学中的泰勒展开式解决该类初等数学问题. 如果函数在定义域上有定义,且有阶导数存在,,则 , 其中,其中介于和间.上式即为函数在点处的泰勒展开式.[1] 令,,有. 上式可以进行放缩,比较和、的大小, 可以得到不等式:,. (*) 下面证明该不等式. 证明:设,,则在单调递减,,即有,当时取等号. 设,,则在单调递减, ,即有,当时取等号. 综上所述,有不等式:,,当时取等号. 如图所示: 例题展示 考题1 (2015年福建卷理科20题) 已知函数 (1) 证明:当时,; (2)证明:当时,存在,使得对任意的,恒有; (3)确定的所有可能取值,使得存在,对任意的,恒有. 解析:(1)在对(*)式的证明过程中已经体现. (1) 设,. 当时,,则在单调递增,则有, 即,此时可以取任意正实数. 当时,令,解得有, 取,则有对任意的,有. 分析:第(2)问的结论可以从图2中解释. (2) 可化为 ,此不等式要求在某个区间成立即可, 而不等式在时恒成立. 因此可以得到,其中, 化简,得,即有,因此有. 考题2 (2015年山东卷理科21题) 设函数,其中. (1)讨论函数的极值点的个数,并说明理由; (2)若成立,求的取值范围. 第(1)问利用导数求函数的极值,需要对进行讨论,这里不再赘述. (2) 由,得, 利用不等式,有, 对上式进行适当放缩,即利用求的取值范围. 当时,,由于在上单调递增,有; 当时,有,此时; 当时,,在上单调递增,有. 综上所述,,要使恒成立,的取值范围.是 考题1的第(3)问,考题2的第(2)问都是恒成立问题,求参数的取值范围.本文这两问的做法,都是先对不等式适当放缩后进行求解,这在平时求解参数范围时是不常见的.之所以这两个题能够利用上述想法进行求解,是因为泰勒展开式的本质上是将一个复杂的函数近似表示为一个多项式函数,是一种函数逼近的思想.该多项式函数与函数之间的误差是非常小的.本文出现的不等式(*)式中的与分别是泰勒展开式的第一项和前两项.这两个函数与函数之间的相差是比较多的,但是在原点附近的较小区间内这两个函数与函数 误差是很小的.因此本文是利用了这一点,对该类问题进行求解.通过放缩将转化成或者这种多项式函数形式,利用多项式函数求参数范围是相对简单的. 应用举例 1 (2014年陕西卷理科21题)设函数.其中是的导函数. (1)令,求的表达式; (2)若恒成立,求实数的取值范围; (3)设,比较与的大小关系,并加以证明. 分析:第(2)问需恒成立, 应用不等式,有, 对上式进行放缩,利用求的取值范围. 当时,上式化简为,此时; 当时,上式化简为,即,则有; 综上所述,有的取值范围是. 2 (2013年全国大纲卷理科22题)已知函数. (1) 若时,求的最小值; (2) 设数列的通项,证明:. 分析:第(1)问需要在时恒成立, 利用不等式,有,该不等式在时取等号对上式进行放缩,利用求的最小值. 当时,上式化简为,此时; 当时,上式化简为,则有; 综上所述,当时,若,则,其最小值为.查看更多