- 2021-04-27 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁省六校协作体2020届高三上学期期中考试数学(文)试卷
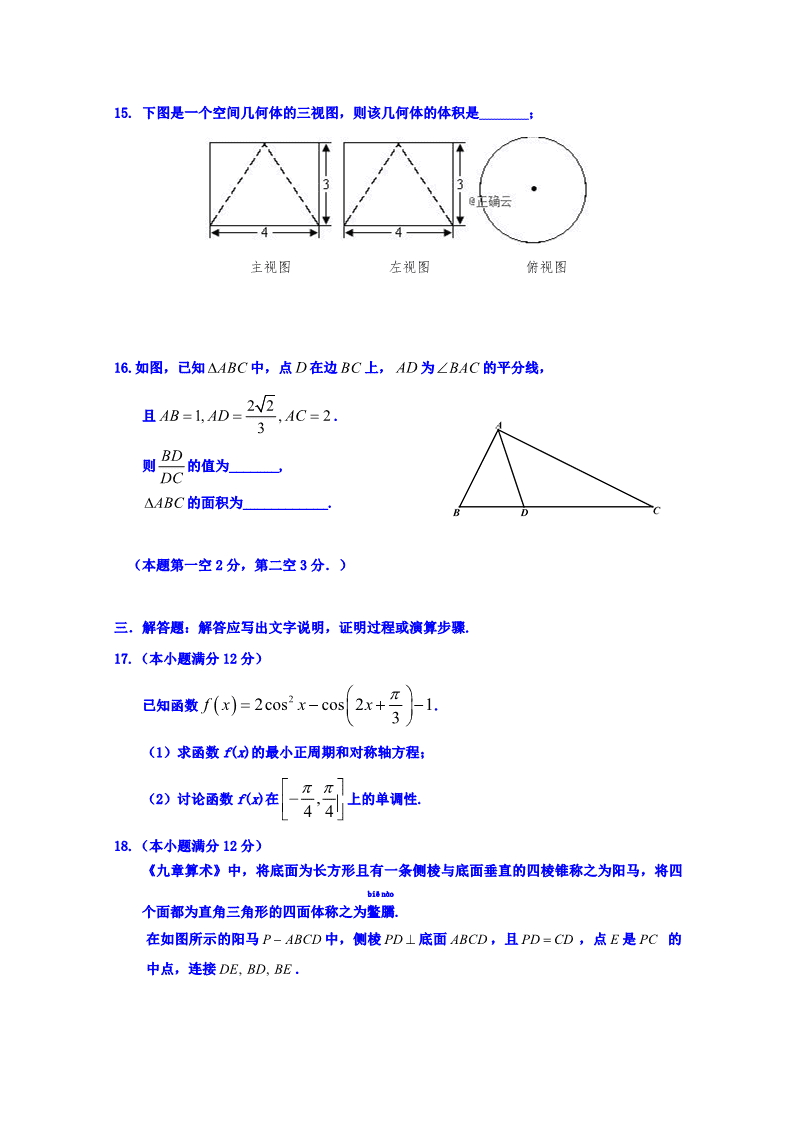
数学试题(文科) 一.选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合 题目要求的. 1. 已知集合 ,则 = ( ) A. B. C. D. 2. 已知 在复平面内对应的点为 P,则 P 点不可能在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3. 若 ,则 ( ) A. B. C. D. 4. 已知 分别是定义在 R 上的偶函数和奇函数,且 =( ) A.-3 B.1 C.-1 D.3 5.在△ABC 中,内角 A,B,C 所对的边分别为 a,b,c,若 ,则角 A 的值为( ) A. B. C. D. 6. 是边长为 的等边三角形,已知向量 , 满足 , ,则下列 结论正确的是( ) A. B. C. D. 7. 若 , 是两条不同的直线, , 是两个不同的平面,则下列命题正确的是( ) A.若 , , ,则 B.若 , , ,则 C.若 , , ,则 D.若 , , ,则 8. 等差数列 的第四项为( ) A. B. C. D. ( ), ( )f x g x 3 2( ) ( ) 1,f x g x x x− = + + (1) (1)f g+则 }24 2 { 6 0{ }P x x Q x x x= − < < = − − <, P Q }{ 4 3x x− < < }4 2{x x− < <− }{ 2 2x x− < < }{ 2 3x x< < ( 3) ( 1)i ( )z m m m R= + + − ∈ 2sin 2 3 α = 1tan tan α α+ = 3 2 2 3 cos cos sinb C c B a A+ = 3 π 6 π 2 π 2 3 π C∆ΑΒ 2 a b 2aΑΒ = C 2a bΑ = + 1=b ba ⊥ (4 )a b BC− ⊥ 1a b⋅ = − m n α β m α⊥ //n β //α β m n⊥ //m α n β⊥ α β⊥ m n⊥ //m α //n β //α β //m n m α⊥ n β⊥ α β⊥ //m n 3 3 3log (2 ),log (3 ),log (4 2),x x x + 3 4 3log 18 3log 24 9.已知三棱锥 中, ,若该三棱锥的 四个顶点在同一个球面上,则此球的体积为( ) A. B. C. D. 10.如图,从气球 上测得正前方的河流的两岸 , 的俯角分别为 , ,此时气球的 高是 ,则河流的宽度 等于( ) A. B. C. D. 11. 关于函数 有下述四个结论: ①f(x)是偶函数 ②f(x)在区间 单调递减 ③f(x)在 有 2 个零点 ④f(x)的最大值为 2 其中所有正确结论的编号是( ) A.①②④ B.②④ C.①④ D.①③ 12. 已知函数 有两个零点 , , ,则下面说法不正确的是 ( ) A. B. C. D.有极小值点 ,且 二.填空题:本大题共 4 小题,每小题 5 分 13. 函数 的值域是_________. 14. 若向量 则 与 夹角的余弦值等于________. ( ) xf x e ax= − 1x 2x 1 2x x< 0x A BCD− 5, 2, 3AB CD AC BD AD BC= = = = = = 3 2 π 24π 6π 6π A B C 75 30 60cm BC 240( 3 1)m− 180( 2 1)m− 120( 3 1)m− 30( 3 1)m+ ( ) cos | | | cos |f x x x= + (0,1) [ , ]−π π 1 2 2x x+ > 1 2 1x x < a e< 1 2 02x x x+ < lg10 xy = (1,2), (1, 1),a b= = − 2a b+ a 15. 下图是一个空间几何体的三视图,则该几何体的体积是 ; 16.如图,已知 中,点 在边 上, 为 的平分线, 且 . 则 的值为_______, 的面积为____________. (本题第一空 2 分,第二空 3 分.) 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分 12 分) 已知函数 . (1)求函数 f(x)的最小正周期和对称轴方程; (2)讨论函数 f(x)在 上的单调性. 18.(本小题满分 12 分) 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四 个面都为直角三角形的四面体称之为 biē 鳖 nào 臑. 在如图所示的阳马 中,侧棱 底面 ,且 ,点 是 的 中点,连接 . 主视图 左视图 俯视图 ABC∆ D BC AD BAC∠ 2 21, , 23AB AD AC= = = BD DC ABC∆ ( ) 22cos cos 2 13f x x x π = − + − ,4 4 π π − P ABCD− PD ⊥ ABCD PD CD= E PC , ,DE BD BE D C A B (1)证明: 平面 (2)证明: 平面 . 试判断四面体 是 否为鳖臑,若是,写出其每个面的直角(只需 写出结论);若不是,请说明理由; (3)记阳马 的体积为 ,四面体 的 体积为 ,求 的值. 19.(本小题满分 12 分) 辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、 丹东四中)中的某校文科实验班的 100 名学生期中考试的语文、数学成绩都不低于 100 分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:[100,110), [110,120),[120,130),[130,140),[140,150]. (1)根据频率分布直方图,估计这 100 名学生语文成绩的中位数和平均数; (同一组数据用该区间的中点值作代表;中位数精确到 0.01) (2)若这 100 名学生语文成绩某些分数段的人数 与数学成绩相应分数段的人数 之比 如下表所示: 分组区间 [100,110) [110,120) [120,130) [130,140) //PA BDE DE ⊥ PBC EBCD P ABCD− 1V EBCD 2V 1 2 V V 0.005 0.030 0.040 频率/组距 成绩(分数)100 120110 130 140 0.020 150 x y 1:3 1:1 3:4 10:1 从数学成绩在[130,150] 的学生中随机选取 2 人,求选出的 2 人中恰好有 1 人数学成 绩在[140,150]的概率. 20.(本小题满分 12 分) 已知数列 、 满足 ,且 (1)令 证明: 是等差数列, 是等比数列; (2)求数列 和 的通项公式; (3)求数列 和 的前 n 项和公式. 21.(本小题满分 12 分) 已知函数 .( 是自然对数的底数, ) (1)讨论 的单调性,并证明 有且仅有两个零点; (2)设 是 的一个零点,证明曲线 在点 处的切线也是曲线 的切线. 请考生在第 22、23 两题中任选一题做答,如果多做,则按所做的第一题记分.做答时用 2B 铅 笔在答题卡上把所选题目对应题号下方的方框涂黑. :x y }{ na }{ nb 1,2 11 == ba 1 1 1 1 4 3 4 ( 2)4 3 4 n n n n n n a a b nb a b − − − − = + + ≥ = + + , ,n n n n n nc a b d a b= + = − { }nc { }nd }{ na { }nb }{ na { }nb 1( ) 1 x xf x e x += + − 2.71828e = ⋅⋅⋅ 1.64872e = ⋅⋅⋅ ( )f x ( )f x 0x ( )f x xy e= 0 0( , )xA x e lny x= 22.(本小题满分 10 分)选修 4—4:坐标系与参数方程 在平面直角坐标系 中,直线 的普通方程是 ,曲线 的参数 方程是 ( 为参数).在以 为极点, 轴的正半轴为极轴建立的极坐 标系中,曲线 的极坐标方程是 . (1)写出 及 的极坐标方程; (2)已知 , , 与 交于 两点, 与 交于 两点, 求 的最大值. 23.(本小题满分 10 分)选修 4—5:不等式选讲 设 , . (1)求证: . (2)求证: . xOy l πtan ( π)2y x α α= < < 1C cos sin x a a y a ϕ ϕ = + = ϕ O x 2C 2 sinbρ θ= l 1C 1 2a = 1b = l 1C ,O M l 2C ,O N 22 | | | || |OM OM ON+ 0, 0, 0a b c> > > 1ab bc ca+ + = 1 1 1a b c bc ca ab a b c + + ≥ + + 3a b c+ + ≥ 数学参考答案(文科) 一、选择题 二、填空题 13、 14、 15、 16、 三、解答题 17. 解:(1) , …………(3 分) 因为 ,所以最小正周期 ,…………(5 分) 令 ,所以对称轴方程为 , .…………(6 分) (2)令 ,得 , , …………(8 分) 设 , , 易知 ,…………(10 分) 所以,当 时, 在区间 上单调递增; 在区间 上单调递减. …………(12 分) ( ) 22cos cos 2 13f x x x π = − + − 1 3cos2 cos2 sin 2 sin 22 2 6x x x x π = − + = + 2ω = 2T π πω= = 2 =6 2x k π π π+ + 6 2 kx π π= + k Z∈ 2 2 22 6 2k x k π π ππ π− + ≤ + ≤ + 3 6k x k π ππ π− + ≤ ≤ + k Z∈ ,4 4A π π = − ,4 6A B π π = − ,4 4x π π ∈ − ( )f x ,4 6 π π − ,6 4 π π 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B D B C D A A C C A C (0, )+∞ 3 10 10 π8 1 ,12 { | , }3 6B x k x k k Z π ππ π= − + ≤ ≤ + ∈ 18. (1)证明:连结 ,交 于 点,连结 ,则 , 又 平面 , 平面 ,所以 平面 .……(3 分) (2)因为 底面 ,所以 . 由底面 为长方形,有 ,而 , 所以 平面 . 平面 ,所以 . 又因为 ,点 是 的中点,所以 . 而 ,所以 平面 . 由 平面 , 平面 ,可知四面体 的四个面都是直角三角形, 即四面体 是一个鳖臑,其四个面的直角分别是 ……(8 分) (3)由已知, 是阳马 的高,所以 ; 由(2)知, 是鳖臑 的高, , 所以 . 在 △ 中,因为 ,点 是 的中点,所以 , 于是 ……(12 分) 19. 解:(1)∵ , , ∴这 100 名学生语文成绩的中位数是 ; …………(3 分) 这 100 名学生语文成绩的平均数是: ……(6 分) (2)∵数学成绩在[100,140)之内的人数为 ∴数学成绩在[140,150]的人数为 人,设为 , , ,……(7 分) 而数学成绩在[130,140)的人数为 人,设为 , ,……(8 分) 从数学成绩在[130,150] 的学生中随机选取 2 人基本事件为: AC BD O OE //PA OE PA ⊄ BDE OE ⊂ BDE //PA BDE PD ⊥ ABCD PD BC⊥ ABCD BC CD⊥ PD CD D= BC ⊥ PCD DE ⊂ PCD BC DE⊥ PD CD= E PC DE PC⊥ PC BC C= DE ⊥ PBC BC ⊥ PCD DE ⊥ PBC EBCD EBCD , , , .BCD BCE DEC DEB∠ ∠ ∠ ∠ PD P ABCD− 1 1 1 3 3ABCDV S PD BC CD PD= ⋅ = ⋅ ⋅ DE D BCE− BC CE⊥ 2 1 1 3 6BCEV S DE BC CE DE∆= ⋅ = ⋅ ⋅ Rt PDC PD CD= E PC 2 2DE CE CD= = 1 2 1 23 4.1 6 BC CD PDV CD PD V CE DEBC CE DE ⋅ ⋅ ⋅= = =⋅⋅ ⋅ 0.05 0.4 0.3 0.75 0.5+ + = > 0.75 0.5 0.25− = 0.25130 10 121.670.3 − × = 105 0.05 115 0.4 125 0.3 135 0.2 145 0.05 123× + × + × + × + × = 4 1(3 0.05 0.4 0.3 0.2) 100 973 10 × + + × + × × = 100 97 3− = 1a 2a 3a 1 0.2 100 210 × × = 1b 2b ( , ),( , ),( , ),( , ),( , ),( , ),( , ),( , ),( , ),( , ),共 10 个, 选出的 2 人中恰好有 1 人数学成绩在[140,150]的基本事件为: ( , ),( , ),( , ),( , ),( , ),( , ),共 6 个, ……(10 分) ∴选出的 2 人中恰好有 1 人数学成绩在[140,150]的概率是 . …………(12 分) 20.(1)证明:由题设得 , 即 ,因此 ,又 , 所以数列 是首项为 3,公差为 2 的等差数列. ……(2 分) 又由题设得 , 即 ,因此 ,又 , 所以数列 是首项为 1,公比为 的等比数列. ……(4 分) (2)由(1)知 ……(6 分) 即 ,解得 ……(7 分) ……(8 分) (3) 的前 n 项和 ,……(10 分) 的前 n 项和 .……(12 分) 21.解:(1) 的定义域为 1a 2a 1a 3a 1a 1b 1a 2b 2a 3a 2a 1b 2a 2b 3a 1b 3a 2b 1b 2b 1a 1b 1a 2b 2a 1b 2a 2b 3a 1b 3a 2b 3 5 1 14( ) 4( ) 8n n n na b a b− −+ = + + 1 1 2n n n na b a b− −+ = + + 1 2( 2)n nc c n−− = ≥ 1 1 1 3c a b= + = { }nc 1 14( ) 2( )n n n na b a b− −− = − 1 12( )n n n na b a b− −− = − 1 1 ( 2)2n nd d n−= ≥ 1 1 1 1d a b= − = { }nd 1 2 112 1, ( ) .2 n n nc n d −= + = 1 2 1 1( )2 n n n n n a b n a b − + = + − = 1 1( ) ,2 2 n na n= + + 1 1( ) .2 2 n nb n= + − { }na 2 112 2n n nS n= + + − { }nb 2 112 2n n nT n= + − + ( )f x { | 1}x x ≠ 2 2( ) 0( 1) xf x e x ′ = + >− 所以 在 上单调递增. ……(2 分) 又 所以 在区间 有唯一零点 ,即 ……(4 分) 又 , 所以 在区间 有唯一零点 . 综上所述, 有且仅有两个零点. ……(6 分) (2)因为 ,所以点 在曲线 上. 由题设 所以直线 的斜率 ……(10 分) 因为曲线 在点 处切线的斜率是 , 曲线 在点 处切线的斜率也是 , 所以曲线 在点 处的切线也是曲线 的切线. …………(12 分) 22. 解:(1)把 , 代入 得 , 所以 极坐标方程是 . 的普通方程是 ,其极坐标方程是 . …………(5 分) (2) : , : , 分别代入 , 得 , . ( )f x ( ,1),(1, )−∞ +∞ 3 2 23(2) 3 0, ( ) 5 0,2f e f e= − > = − < ( )f x (1, )+∞ 1x 1 1 1 1 1( ) 0. 1 x xf x e x += = −即 1 1 1 1 1 1 1 1 1 1 1 11, ( ) 01 1 1 x x x xx f x e x x x − − − −− < − − = + = + =+ + + ( )f x ( ,1)−∞ 1x− ( )f x 0 0ln xe x− = − 0 0( , )xB e x− − lny x= 0 0 0 0 1( ) 0, 1 x xf x e x += = −即 AB 0 0 0 0 0 0 0 0 00 0 0 0 1 1 1 .1 1 1 x x x x xe x x xk exx e xx x − + ++ − += = = =−− −− + xy e= 0 0( , )xA x e 0xe lny x= 0 0( , )xB e x− − 0xe xy e= 0 0( , )xA x e lny x= cosx ρ θ= siny ρ θ= tany x α= tan tanθ α= l π( , π)2 θ α ρ α= ∈ <查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档