【数学】2020届一轮复习浙江版综合检测二
综合检测二
(时间:120分钟 满分:150分)
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
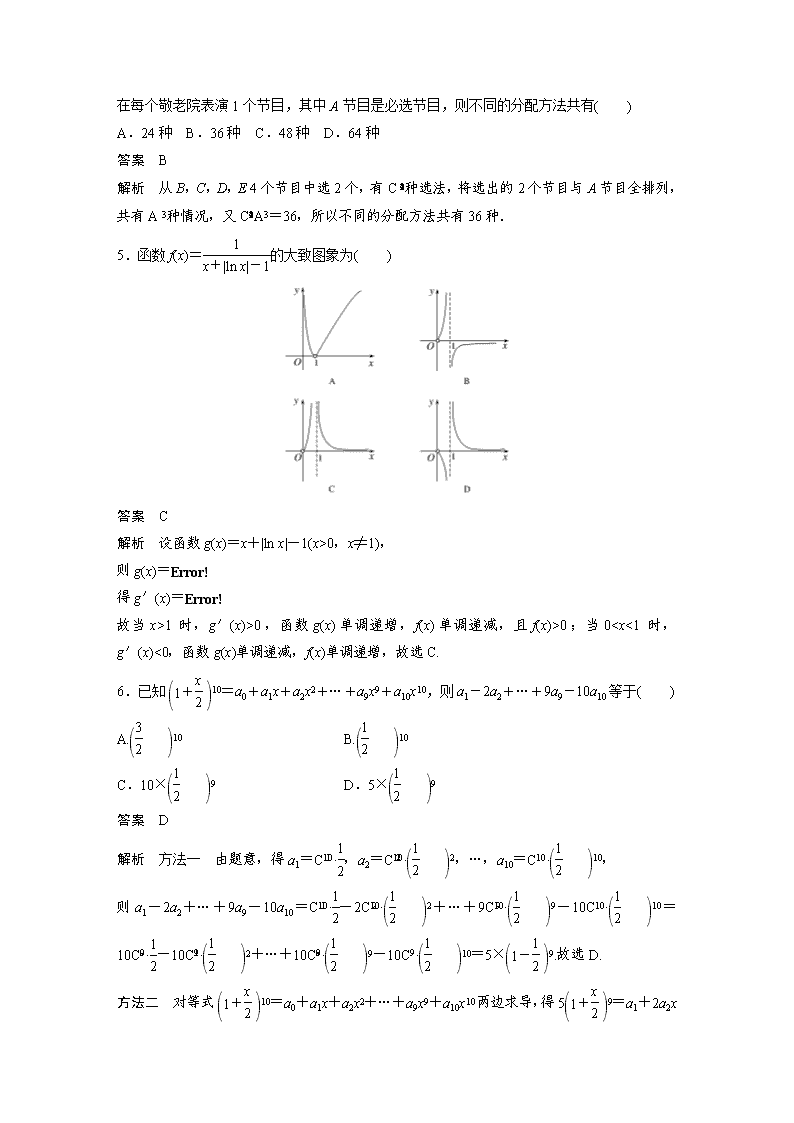
1.已知集合A={x|-2
0,x≠1),
则g(x)=
得g′(x)=
故当x>1时,g′(x)>0,函数g(x)单调递增,f(x)单调递减,且f(x)>0;当0D(X)+D(Y)
D.E(X)+E(Y)2x2y2=D(X)+D(Y),
E(X)+E(Y)=3>≥(x2y2)2=D(X)·D(Y),故选C.
8.已知向量a,b满足|2a+b|=3,且a·(a-b)=3,则|a-b|的最小值为( )
A. B. C. D.
答案 D
解析 方法一 由a·(a-b)=3,
得[(2a+b)+(a-b)]·(a-b)=9,
即(2a+b)·(a-b)+|a-b|2=9,
设2a+b与a-b的夹角为θ,
则(2a+b)·(a-b)=|2a+b|·|a-b|·cos θ∈[-3|a-b|,3|a-b|],
所以-3|a-b|≤9-|a-b|2≤3|a-b|,
解得≤|a-b|≤,
所以|a-b|的最小值为.
方法二 如图,设a=,b=,
由|2a+b|=3,
得=1,
取靠近A的AB的三等分点C,
则=a+b,所以||=1.
由a·(a-b)=3,得·=1.
以MC所在直线为x轴,线段MC的垂直平分线为y轴,建立平面直角坐标系xOy,则M,C,
设A(x,y),则由·=1,得x2+y2=,
所以点A的轨迹是以O(0,0)为圆心,为半径的圆,
易知点C在该圆内,所以|AC|的最小值为,
所以|AB|的最小值为,
即|a-b|的最小值为.
9.已知P为双曲线-=1上一点,M,N分别为圆(x+3)2+y2=及其关于y轴对称的圆上的两点,则|PM|-|PN|的取值范围为( )
A.[-5,5] B.[-5,-3]∪[3,5]
C.(-3,3) D.[-3,3]
答案 B
解析 由题意知,点M在圆(x+3)2+y2=上,点N在圆(x-3)2+y2=上,设双曲线-=1的左、右焦点分别为F1,F2,则F1(-3,0),F2(3,0),易知F1,F2分别为两个圆的圆心,连接PF1,MF1,PF2,NF2,则|PF1|-|MF1|≤|PM|≤|PF1|+|MF1|,|PF2|-|NF2|≤|PN|≤|PF2|+|NF2|,所以|PF1|-|PF2|-1≤|PM|-|PN|≤|PF1|-|PF2|+1,而|PF1|-|PF2|=±4,所以-5≤|PM|-|PN
|≤-3或3≤|PM|-|PN|≤5.
10.如图1,已知正三角形ABC的边长为6,O是底边BC的中点,D是AB边上一点,且AD=2,将△AOC绕着直线AO旋转,在旋转过程中,若DC的长度在[,]内变化,如图2,则点C所形成的轨迹的长度为( )
A. B. C.π D.
答案 A
解析 方法一 ∵△ABC为正三角形,O为BC的中点,
∴AO⊥OB,AO⊥OC,
∴∠BOC是二面角B-AO-C的平面角,记∠BOC=θ.
如图,过点D作DE⊥OB,垂足为E,连接CE,则DE∥AO,OE=1,OC=3,DE=AO=2,则=++,其中〈·〉=θ,
即〈,〉=π-θ,
∴2=(++)2=2+2+2+2·=(2)2+12+32+2×1×3×cos〈,〉=22-6cos θ,
则2=22-6cos θ∈[19,22],即cos θ∈,
即点C转过的角度为-=.
点C的轨迹为以O为圆心,以OC为半径的一段圆弧,弧长为3×=.
方法二 ∵△ABC为正三角形,O为BC的中点,
∴AO⊥OB,AO⊥OC,
∴∠BOC是二面角B-AO-C的平面角,记∠BOC=θ.
如图,过点D作DE⊥OB,垂足为E,连接CE,则DE∥AO,OE=1,OC=3,DE=AO=2,则EC2=OC2+OE2-2OC·OE·cos θ=10-6cos θ,
在Rt△DCE中,DC2=DE2+EC2=(2)2+10-6cos θ=22-6cos θ,则DC2=22-
6cos θ∈[19,22],
即cos θ∈,即点C转过的角度为-=.
点C的轨迹为以O为圆心,以OC为半径的一段圆弧,弧长为3×=.
第Ⅱ卷(非选择题 共110分)
二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.把答案填在题中横线上)
11.《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早一千年.在《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”.已知某“鳖臑”的三视图(单位:cm)如图所示,则该“鳖臑”的体积是________ cm3.
答案 10
解析 由三视图结合“鳖臑”的定义易得该几何体为一个底面为直角边长分别为3,4,高为5,且顶点在底面的射影为直角三角形中最小的角的顶点,则其体积为××3×4×5=10 cm3.
12.已知等比数列{an}的公比q>0,前n项和为Sn.若2(a5-a3-a4)=a4,且a2a4a6=64,则q=________,Sn=________.
答案 2
解析 ∵2(a5-a3-a4)=a4,
∴2a5=2a3+3a4⇒2q4=2q2+3q3⇒2q2-3q-2=0,
得q=-(舍去)或q=2.
∵a2a4a6=64,∴a=64⇒a4=4,
∴a1=,Sn==.
13.已知x,y满足约束条件则约束条件表示的可行域的面积为________,目标函数z=x-y+3的取值范围为________.
答案 [2,3]
解析 画出可行域如图中阴影部分(含边界)所示,则A(0,1),B(2,2),C,
易知AC⊥BC,
则可行域的面积
S=·|AC|·|BC|=.
因为z=x-y+3,所以y=x-z+3,
数形结合知,当直线y=x-z+3与直线BC重合时,z取得最大值3,当直线y=x-z+3经过点A时,z取得最小值2,所以z∈[2,3].
14.已知函数f(x)=|2x-1|,g(x)=|2x+a|(a∈R),则不等式f(x)≤3的解集为________;若不等式f(x)+g(x)≥6对任意的x∈R恒成立,则实数a的取值范围是________________________.
答案 [-1,2] (-∞,-7]∪[5,+∞)
解析 f(x)≤3,即|2x-1|≤3,即-3≤2x-1≤3,
解得-1≤x≤2,
所以不等式f(x)≤3的解集为[-1,2].
因为f(x)+g(x)=|2x-1|+|2x+a|
≥|2x-1-2x-a|=|a+1|,
所以要使不等式f(x)+g(x)≥6对任意的x∈R恒成立,则|a+1|≥6,解得a≤-7或a≥5.
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a=3,b=2,A=2B,则sin B=________,c=________.
答案
解析 ∵a=3,b=2,A=2B,
∴由正弦定理=得,
=,即=,
∵B为△ABC的一个内角,∴sin B>0,∴cos B=,
∴sin B==.
由二倍角公式知,
sin A=sin 2B=2sin Bcos B=2××=,
cos A=cos 2B=2cos2B-1=.
方法一 ∵cos C=cos[π-(A+B)]=-cos(A+B)
=-(cos Acos B-sin Asin B)=,
∴c2=a2+b2-2abcos C=,∴c=.
方法二 ∵sin C=sin[π-(A+B)]=sin(A+B)
=sin Acos B+cos Asin B=,
由正弦定理=,得=,∴c=.
16.已知x,y,z均为正实数,且满足x2+y2+z2=1,则xy+2yz的最大值为________.
答案
解析 由已知条件x2+y2+z2=1,
可设1=x2+λy2+(1-λ)y2+z2,0<λ<1,
即得1≥2xy+2yz,
令=,解得λ=,
所以xy+yz≤1,即xy+2yz≤,
当且仅当即时等号成立.
17.已知函数f(x)=x+,若对于任意的m∈R,方程|f(m+x)|+|f(m-x)|=a均有解,则a
的取值范围是________.
答案 [4,+∞)
解析 令g(x)=|f(m+x)|+|f(m-x)|,
∴g(-x)=|f(m-x)|+|f(m+x)|=g(x),
∴g(x)是偶函数,设x>0,
①若m>0,
当x2≥4;
当x>m时,g(x)=(x+m)++(x-m)+=2x++=2x+>2≥4.
②若m<0,则-m>0,
当x<-m时,g(x)=-(x+m)--(m-x)-
=-2m-=-2m-
>2≥4;
当x>-m时,g(x)=(x+m)++(x-m)+=2x++=2x+>2≥4.
③若m=0,g(x)=2≥4.
又g(x)是偶函数,∴当x<0时,g(x)=g(-x)≥4.
综上,g(x)≥4.
∴要使方程g(x)=a有解,只需a≥4即可,
∴所求a的取值范围是[4,+∞).
三、解答题(本大题共5小题,共74分.解答应写出文字说明,证明过程或演算步骤)
18.(14分)(2019·台州模拟)设函数f(x)=sin-2sin xcos x(x∈R).
(1)求函数f(x)的最小正周期及f的值;
(2)将函数f(x)的图象向右平移个单位长度,得到函数g(x)的图象,试求g(x)在上的最小值.
解 (1)f(x)=sin-2sin xcos x
=sin 2x+cos 2x-sin 2x
=cos 2x-sin 2x=cos.
所以函数f(x)的最小正周期T==π,
f=cos=-.
(2)g(x)=f=cos
=cos.
因为x∈,所以2x+∈.
所以当2x+=π,即x=时,g(x)取最小值,此时g(x)min=-1.
19.(15分)如图,在四棱锥P-ABCD中,DB⊥平面PAB,∠ABP=120°,AB∥CD,CD=BD=AB=BP=2,E为AP的中点.
(1)求证:PC∥平面BDE;
(2)求直线DE与平面PCD所成角的正弦值.
(1)证明 方法一 连接AC交BD于点F,连接EF,
则EF为△ACP的中位线,所以EF∥PC,
又EF⊂平面BDE,PC⊄平面BDE,
所以PC∥平面BDE.
方法二 因为AB∥CD,AB=CD,
所以四边形ABCD为平行四边形,
所以AD∥BC且AD=BC,
故可将四棱锥P-ABCD补形成三棱柱PAB-KDC,如图,取DK的中点Q,连接QC,PQ,EQ.
易知DQ∥EP,DQ=EP,
所以四边形PEDQ为平行四边形,所以DE∥PQ,
又DE⊂平面BDE,PQ⊄平面BDE,所以PQ∥平面BDE.
又DQ∥AE,DQ=AE,
所以四边形ADQE为平行四边形,
所以AD∥EQ,AD=EQ,
又AD∥BC,AD=BC,∴EQ∥BC,EQ=BC,
所以四边形BEQC为平行四边形,所以BE∥QC,
又BE⊂平面BDE,QC⊄平面BDE,
所以QC∥平面BDE.
又PQ∩QC=Q,所以平面PQC∥平面BDE.
又PC⊂平面PQC,所以PC∥BDE.
(2)解 方法一 由(1)中方法二可知DE∥PQ,
所以直线DE与平面PCD所成的角就是直线PQ与平面PCD所成的角,设直线PQ与平面PCD所成的角为θ,点Q到平面PCD的距离为h.
连接AC交BD于点F,连接EF,
易知EF=,PC=2,PQ=,
在△CDP中,DP=2=PC,CD=2,
所以S△CDP=×2×=,
易知S△CDQ=×1×=,
因为VP-CDQ=VQ-CDP,
所以×S△CDQ×BD=×S△CDP×h,
所以h=.所以sin θ===,
所以直线DE与平面PCD所成角的正弦值为.
方法二 在△BAP中,AB=BP=2,E为AP的中点,∠ABP=120°,所以BE⊥AP,
以E为坐标原点,,的方向分别为x,y轴的正方向,过点E且平行于DB的直线为z轴,且的方向为z轴的正方向建立空间直角坐标系(图略),则E(0,0,0),B(1,0,0),A(0,,0),P(0,-,0),D(1,0,2),
所以=(1,,2),==(1,-,0),=(1,0,2),
设直线DE与平面PCD所成的角为θ,平面PCD的法向量为n=(x,y,z),则得
取y=1,得x=,z=-,
所以n=(,1,-)为平面PCD的一个法向量,
所以sin θ===,
所以直线DE与平面PCD所成角的正弦值为.
20.(15分)已知等差数列{an}的前n项和为Sn,且a2n=2an+3,S3=3,数列{bn}为等比数列,b1+b3=10a3,b2+b4=10a6.
(1)求数列{an},{bn}的通项公式;
(2)若cn=,求数列{cn}的前n项和Tn,并求使得Tn<λ2-λ恒成立的实数λ的取值范围.
解 (1)由{an}为等差数列可得,
S3=a1+a2+a3=3a2=3,故a2=1.
由a2n=2an+3可得a2=2a1+3,
故1=2a1+3,解得a1=-1.
所以数列{an}的公差d=a2-a1=1-(-1)=2,
所以an=a1+(n-1)d=-1+2(n-1)=2n-3.
故a3=2×3-3=3,a6=2×6-3=9.
设等比数列{bn}的公比为q,
则由已知可得b1+b3=10a3=30,b2+b4=10a6=90.
所以q===3,
故b1+b3=b1+b1×32=30,解得b1=3.
所以数列{bn}的通项公式为bn=3×3n-1=3n.
(2)由(1)可知,cn=
=×
=×
=.
所以Tn=c1+c2+…+cn
=++…+
=
=
=.
因为>0,所以Tn<×=.
故由Tn<λ2-λ恒成立可得λ2-λ≥,
即64λ2-4λ-3≥0,也就是(4λ-1)(16λ+3)≥0,
解得λ≤-或λ≥.
21.(15分)如图,已知在平面直角坐标系xOy中,抛物线E:x2=2py(p>0)的焦点F是椭圆C:+y2=1的一个焦点.
(1)求抛物线E的方程;
(2)设P是E上的动点,且位于第一象限,抛物线E在点P处的切线l与椭圆C
交于不同的两点A,B,直线y=-与过点P且垂直于x轴的直线交于点M,OM与直线l交于点D.
①求证:直线OM平分线段AB;
②若直线l与y轴交于点G,记△PFG的面积为S1,△PDM的面积为S2,是否存在点P,使得取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(1)解 根据题意,F,
所以抛物线E的方程为x2=2y.
(2)①证明 设P(m>0),
由x2=2y可得y′=x,所以直线l的斜率为m,
因此直线l的方程为y-=m(x-m),即y=mx-.
设A(x1,y1),B(x2,y2),
由得(3m2+4)x2-3m3x+-3=0,
所以x1+x2=.
又M,所以OM的方程为y=-x,
由得直线OM与l的交点的横坐标为
xD=,故xD=,
所以直线OM平分线段AB.
②解 由①知直线l的方程为y=mx-(m>0),
所以G,所以P,F,
D,M,
所以S1=|GF|m=m(m2+1),
S2=|PM|·|m-xD|=,
所以=.
令t=3m2+8,则==402-,
又对于(3m2+4)x2-3m3x+-3=0,Δ>0,
即(-3m3)2-4(3m2+4)>0,
所以00,f′(x)>0,
所以f(x)的单调递增区间为(-∞,+∞).
②当a>0时,Δ=(4a)2-4a(2a+1)=4a(2a-1),
(i)当a>时,Δ>0,令u(x)=0,得
x1=,x2=,且x10,f′(x)>0,
当x∈(x1,x2)时,u(x)<0,f′(x)<0,
所以f(x)的单调递增区间为,,单调递减区间为.
(ii)当00,令u(x)=0,得
x1=,x2=,且x20,f′(x)>0,
当x∈(-∞,x2)∪(x1,+∞)时,u(x)<0,f′(x)<0,
所以f(x)的单调递增区间为
,单调递减区间为,.
综上,当a>时,f(x)的单调递增区间为,,单调递减区间为;
当0≤a≤时,f(x)的单调递增区间为(-∞,+∞);
当a<0时,f(x)的单调递增区间为,单调递减区间为,.
(2)证明 方法一 由(1)得,x1=,
x2=.
①当a≤-时,由(1)知f(x)在(x1,+∞)上单调递减,
因为x1==-2+ ≤0,
所以f(x)在(0,+∞)上单调递减,
所以当x≥0时,f(x)≤f(0)=-1<0.
②当-0,g(x)在(ln 2,1)上单调递增,
因为g(0)=-1<0,g(1)=2e-7<0,
所以当x∈(0,1)时,恒有g(x)<0.
又x1∈(0,1),所以g(x1)<0,即f(x1)<0,
从而当x≥0时,f(x)≤f(x1)<0.
综上,若a<-,当x≥0时,f(x)<0.
方法二 f(x)=(ax2+2ax+1)ex-2=aex(x2+2x)+ex-2,
令φ(a)=aex(x2+2x)+ex-2,
显然当x≥0时,ex(x2+2x)≥0,
所以当a<-时,φ(a)<φ=-+ex-2.
所以要证当x≥0时,f(x)<0,
只需证当x≥0时,-+ex-2≤0,
即证当x≥0时,ex(x2+2x-7)+14≥0.
令g(x)=ex(x2+2x-7)+14,
则g′(x)=ex(x2+4x-5)=(x-1)(x+5)ex,
所以当x∈(0,1)时,g′(x)<0,g(x)在(0,1)上单调递减,当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上单调递增,
所以当x≥0时,g(x)≥g(1)=14-4e>0,
从而当x≥0时,f(x)<0.