2021届课标版高考文科数学大一轮复习课件：§1-2 命题及其关系、充分条件与必要条件（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§1-2 命题及其关系、充分条件与必要条件（讲解部分）

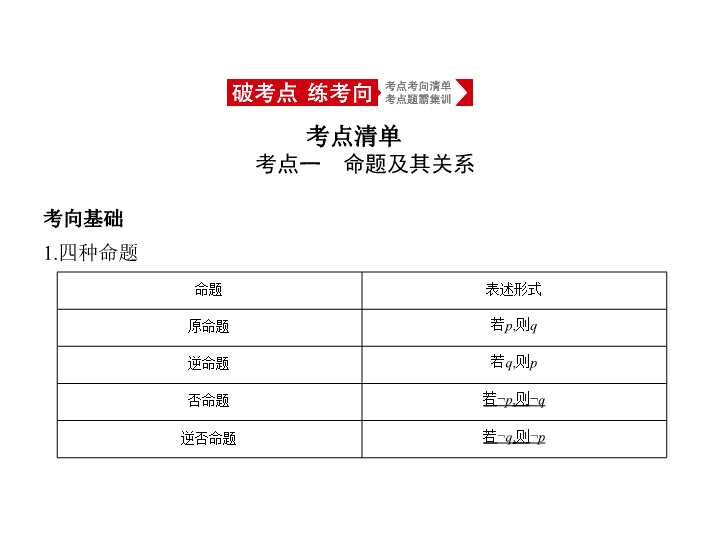
考点一　命题及其关系 考点清单 考向基础 1.四种命题 命题 表述形式 原命题 若 p ,则 q 逆命题 若 q ,则 p 否命题 若¬ p ,则¬ q 逆否命题 若¬ q ,则¬ p 2.四种命题间的关系   3.四种命题的真假关系 (1)两个命题互为逆否命题, 它们有相同的真假性 ; (2)两个命题互为逆命题或互为否命题,它们的 真假性没有关系 . 【知识拓展】 1.否命题与命题的否定的区别 (1)否命题是对原命题的 条件和结论同时否定 ; (2)命题的否定仅 否定原命题的结论,条件不变 . 因此否命题与命题的否定是两种不同的命题. 2.常用的正面叙述词语和它的否定词语 正面 词语 等于 (=) 大于 (>) 小于 (<) 是 都是 任意的 所有的 至多有 一个 至少有 一个 否定 词语 不等于 ( ≠ ) 不大于 ( ≤ ) 不小于 ( ≥ ) 不是 不都是 某个 某些 至少有 两个 一个也 没有 考向一　四种命题的互化 考向突破 例1    (2019豫南九校3月联考,2)下列命题中为真命题的是   (　　) A.命题“若 x >1,则 x 2 >1”的否命题 B.命题“若 x > y ,则 x >| y |”的逆命题 C.命题“若 x =1,则 x 2 + x -2=0”的否命题 D.命题“若   >1,则 x >1”的逆否命题 解析　对于A,否命题为“若 x ≤ 1,则 x 2 ≤ 1”,易知当 x =-2时, x 2 =4>1,故否命 题为假命题;对于B,逆命题为“若 x >| y |,则 x > y ”,易知其为真命题;对于C,否 命题为“若 x ≠ 1,则 x 2 + x -2 ≠ 0”,易知当 x =-2时, x 2 + x -2=0,故否命题为假命 题;对于D,逆否命题为“若 x ≤ 1,则   ≤ 1”,易知其为假命题,故选B. 答案    B 例2　下列命题正确的有 　　　     (填写所有正确命题的序号). ①“若log 2 a >0,则函数 f ( x )=log a x ( a >0,且 a ≠ 1)在其定义域内是减函数”是 真命题; ②命题“若 a =0,则 ab =0”的否命题是“若 a ≠ 0,则 ab ≠ 0”; ③命题“若 x , y 都是偶数,则 x + y 也是偶数”的逆命题为真命题; ④命题“若 a ∈ M ,则 b ∉ M ”与命题“若 b ∈ M ,则 a ∉ M ”等价. 考向二　命题的真假判断 解析　对于①,若log 2 a >0,则 a >1,所以函数 f ( x )=log a x ( a >0,且 a ≠ 1)在其定义 域内是增函数,故①不正确;易知②正确;对于③,原命题的逆命题是“若 x + y 是偶数,则 x , y 都是偶数”,易知其为假命题,如1+3=4是偶数,但3和1均为奇 数,故③不正确;对于④,命题“若 a ∈ M ,则 b ∉ M ”与命题“若 b ∈ M ,则 a ∉ M ”互为逆否命题,因此二者等价,所以④正确.综上,可知正确的有②④. 答案　②④ 考点二　充分条件与必要条件 考向基础 1.充分条件与必要条件 (1)如果 p ⇒ q ,则 p 是 q 的 充分条件 , q 是 p 的 必要条件 ; (2)如果 p ⇒ q , q ⇒ p ,则 p 是 q 的 充要条件 . 2.充分条件与必要条件的两种判断方法 条件 定义法 集合法: A ={ x | p ( x )}, B ={ x | q ( x )} p 是 q 的充分条件 p ⇒ q A ⊆ B p 是 q 的必要条件 q ⇒ p A ⊇ B p 是 q 的充要条件 p ⇒ q 且 q ⇒ p A = B p 是 q 的充分不必要条件 p ⇒ q 且 q ⇒ / p A ⫋ B p 是 q 的必要不充分条件 p ⇒ / q 且 q ⇒ p A ⫌ B p 是 q 的既不充分也不必要条件 p ⇒ / q 且 q ⇒ / p A ⊈ B 且 A ⊉ B 3.充分条件与必要条件的两个性质 (1)若 p 是 q 的充分条件,则 q 是 p 的必要条件. (2)传递性:若 p 是 q 的充分条件, q 是 r 的充分条件,则 p 是 r 的充分条件. 【知识拓展】 “ p 是 q 的充分不必要条件”与“ p 的一个充分不必要条件是 q ”两者不同, 前者是“ p ⇒ q 且 q ⇒ / p ”,而后者是“ q ⇒ p 且 p ⇒ / q ”. 考向一　充分条件与必要条件的判断 考向突破 例3    (2020届安徽江南十校尖子生联考,4)下列说法正确的是   (　　) A.“ x =-1”是“ x 2 -5 x -6=0”的必要不充分条件 B. p : A ∩ B = A , q : A ⫋ B ,则 p 是 q 的充分不必要条件 C.已知数列{ a n },若 p :对于任意的 n ∈N * ,点 P n ( n , a n )都在直线 y =2 x +1上; q :{ a n } 为等差数列,则 p 是 q 的充要条件 D.“ x <0”是“ln( x +1)<0”的必要不充分条件 解析　对于选项A,由 x 2 -5 x -6=0,解得 x =-1或 x =6,所以“ x =-1”是“ x 2 -5 x -6= 0”的充分不必要条件,故A错误.对于选项B,由 A ∩ B = A ,得 A ⊆ B ,所以 p 是 q 的必要不充分条件,故B错误.对于选项C,∵点 P n ( n , a n )在直线 y =2 x +1上,∴ a n =2 n +1( n ∈N * ),由 a n +1 - a n =2( n +1)+1-2 n -1=2,且 n ∈N * 可知数列{ a n }是公差为2 的等差数列,即 p ⇒ q ;反之不成立,如,令 a n = n ,则{ a n }为等差数列,但点( n , n )不 在直线 y =2 x +1上,即 q ⇒ / p ,所以 p 是 q 的充分不必要条件,故C错误.对于选项 D,由ln( x +1)<0得0< x +1<1,解得-1< x <0,所以“ x <0”是“ln( x +1)<0”的必要 不充分条件,故D正确.故选D. 答案    D 例4　设命题 p :|4 x -3| ≤ 1,命题 q : x 2 -(2 a +1) x + a ( a +1) ≤ 0,若¬ p 是¬ q 的必要不充 分条件,则实数 a 的取值范围是   (　　) A.   　     B.   C.(- ∞ ,0] ∪   　    D.(- ∞ ,0) ∪   考向二　由充分、必要条件求参数的取值范围 解析    设 A ={ x ||4 x -3| ≤ 1}, B ={ x | x 2 -(2 a +1) x + a ( a +1) ≤ 0}. 解|4 x -3| ≤ 1,得   ≤ x ≤ 1, 故 A =   , 解 x 2 -(2 a +1) x + a ( a +1) ≤ 0,得 a ≤ x ≤ a +1, 故 B ={ x | a ≤ x ≤ a +1}. 解法一:¬ p 所对应的集合为 ∁ R A =   ,¬ q 所对应的集合为 ∁ R B = { x | x < a 或 x > a +1}. 由¬ p 是¬ q 的必要不充分条件,知 ∁ R B ⫋∁ R A , ∴   或   解得0 ≤ a ≤   . ∴实数 a 的取值范围是   . 解法二:∵¬ p 是¬ q 的必要不充分条件, ∴ q 是 p 的必要不充分条件, 即 p 是 q 的充分不必要条件. ∴ A ⫋ B , ∴   或   解得0 ≤ a ≤   . ∴实数 a 的取值范围为   .故选A. 答案    A 方法1　 四种命题及其真假的判定方法 1.给出一个命题,要判定它是真命题,需经过严格的推理证明;而要说明它是 假命题,只需举一反例即可. 2.掌握原命题和逆否命题,否命题和逆命题的等价性,当直接判断一个命题 的真假不易进行时,可以判断其逆否命题的真假. 方法技巧 例1    (2019陕西西北工大附中模拟,5)给出命题:“已知 a , b , c , d 是实数,若 a ≠ b 或 c ≠ d ,则 a + c ≠ b + d ”,对原命题、逆命题、否命题、逆否命题而言,其 中真命题的个数为   (　　) A.1　    B.2　    C.3　    D.4         解题导引    解析　由原命题得其逆否命题为“已知 a , b , c , d 是实数,若 a + c = b + d ,则 a = b 且 c = d ”,取 a =1, b =2, c =3, d =2,则满足1+3=2+2,但不满足 a = b 且 c = d ,故逆否命题 为假命题;而原命题的否命题为“已知 a , b , c , d 是实数,若 a = b 且 c = d ,则 a + c = b + d ”,易得其为真命题.根据原命题与逆否命题,逆命题与否命题都是互为 逆否关系,真假性相同,可知4个命题中的真命题有2个,故选B. 答案    B 方法2 　充分条件与必要条件的判定方法 1. 定义法 (1)分清条件和结论:分清哪个是条件,哪个是结论; (2)找推式:判断“ p ⇒ q ”及“ q ⇒ p ”的真假; (3)下结论:根据推式及定义下结论. 2. 集合法 根据 p , q 成立对应的集合之间的包含关系进行判断. 3. 等价转化法 等价转化法适用于条件和结论带有否定性词语的命题或直接判断不方便 的情况,具体方法是通过判断原命题的逆否命题的真假来间接判断原命题 的真假.常用结论如下: (1)¬ q 是¬ p 的充分不必要条件 ⇔ p 是 q 的充分不必要条件; (2)¬ q 是¬ p 的必要不充分条件 ⇔ p 是 q 的必要不充分条件; (3)¬ q 是¬ p 的充要条件 ⇔ p 是 q 的充要条件; (4)¬ q 是¬ p 的既不充分也不必要条件 ⇔ p 是 q 的既不充分也不必要条件. 例2    (2017天津,4,5分)设 θ ∈R,则“   <   ”是“sin θ <   ”的   (　　) A.充分而不必要条件　    B.必要而不充分条件 C.充要条件　      D.既不充分也不必要条件 解析　解法一(集合法):   <   ⇔ -   < θ -   <   ⇔ 0< θ <   ; sin θ <   ⇔ -   +2 k π< θ <   +2 k π, k ∈Z. 由   ⫋   , k ∈Z, 可得“   <   ”是“sin θ <   ”的充分不必要条件. 解法二(定义法):   <   ⇔ 0< θ <   ⇒ sin θ <   ,当 θ =0时,sin θ <   ,但不满足   <   ,所以是充分不必要条件,故选A. 答案    A