- 2021-04-27 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
反比例函数的图象和性质2
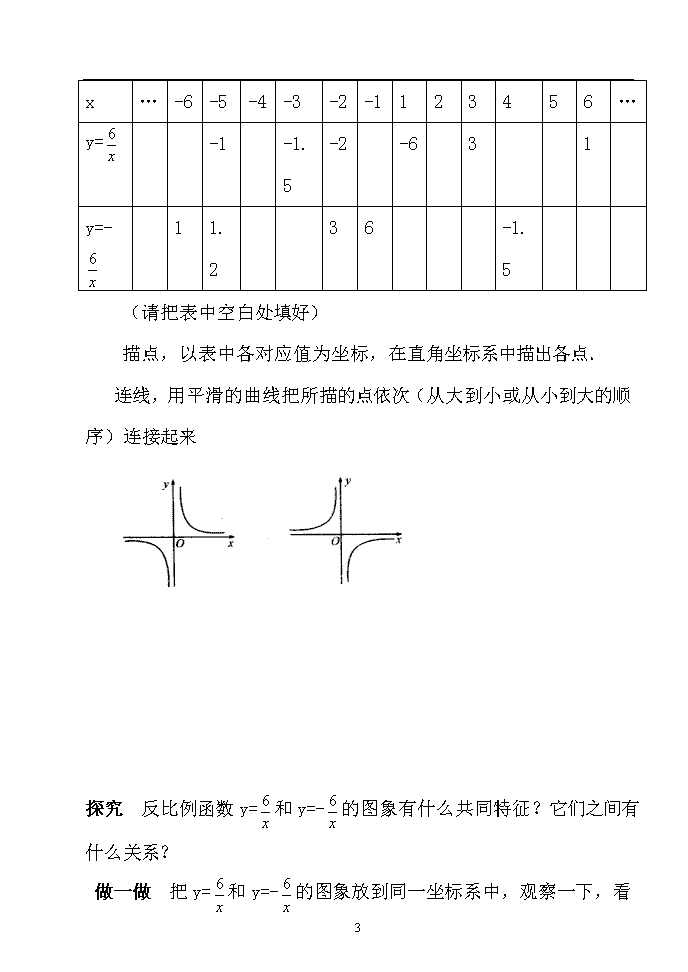
26.1.2 反比例函数的图象和性质 知能准备 【学习目标】1、画反比例函数的图象,并知道该图象与正比例函数、一次函数图象的区别,能从反比例函数的图象上分析出简单的性质. 2、能用反比例函数的定义和性质解决实际问题. 【学情分析】前面已经学习了一次函数和二次函数,对研究函数有了一定的方法;即画出图像 并根据图像研究其性质 【学思指导】教法:讲授法、对比法 学法:类比法、数形结合法 学科素养:通过画图象,进一步培养“描点法”画图的能力和方法,并提高对函数图象的分析能力.同时尝试用类比和特殊到一般的思路方法,归纳反比例函数一些性质特征. 【板书设计】 30.2反比例函数的图像和性质(一) 画图: 画图: 性质 步骤: 步骤: 8 图像: 图像: 【课前预习】 1.若y=是反比例函数,则n必须满足条件 n≠或n≠-1 . 2.用描点法画图象的步骤简单地说是 列表 、 描点 、 连线 . 3.试用描点法画出下列函数的图象:(1)y=2x; (2)y=1-2x. 设计意图:通过回忆,学会用描点法画函数的图象 课堂引讨——【展示互动】 问题:我们已知道,一次函数y=kx+b(k≠0)的图象是一条直线,那么反比例函数y=(k为常数且k≠0)的图象是什么样呢? [尝试] 用描点法来画出反比例函数的图象. 画出反比例函数y=和y=-的图象. 解:列表 思考:取什么值更易描出来 8 x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 … y= -1 -1.5 -2 -6 3 1 y=- 1 1.2 3 6 -1.5 (请把表中空白处填好) 描点,以表中各对应值为坐标,在直角坐标系中描出各点. 连线,用平滑的曲线把所描的点依次(从大到小或从小到大的顺序)连接起来 探究 反比例函数y=和y=-的图象有什么共同特征?它们之间有什么关系? 做一做 把y=和y=- 8 的图象放到同一坐标系中,观察一下,看它们是否对称. 归纳: 反比例函数y=和y=-的图象的共同特征: (1)它们都由两条曲线组成. (2)随着x的不断增大(或减小),曲线越来越接近坐标轴(x轴、y轴). (3)反比例函数的图象属于双曲线. 此外,y=的图象和y=-的图象关于x轴对称,也关于y轴对称. 做一做 在平面直角坐标系中画出反比例函数y=和y=-的图象. 交流 两个函数图象都用描点法画出? 【分析】 由y=和y=-的图象及y=和y=-的图象知道, (1)它们有什么共同特征和不同点? (2)每个函数的图象分别位于哪几个象限? (3)在每一个象限内,y随x的变化而如何变化? 猜想 反比例函数y=(k≠0)的图象在哪些象限由什么因素决定?在每一个象限内,y随x的变化情况如何?它可能与坐标轴相交吗? 【归纳】 (1)反比例函数y=(k为常数,k≠0)的图象是双曲线. 8 (2)当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内,y值随x值的增大而减小. (3)当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内,y值随x值的增大而增大. 设计意图:通过画图并研究:得到反比例函数图像的形状及其增减性 精编精练 例题 指出当k>0时,下列图象中哪些可能是y=kx与y=(k≠0)在同一坐标系中的图象 ( ) 【分析】 对于y=kx来说,当k>0时,图象经过一、三象限,当k<0时,图象经过二、四象限;对于y=来说,当k>0时,图象在一、三象限,当k<0时,图象在二、四象限,所以应选B. 备选例题 8 1.请你写出一个反比例函数的解析式,使它的图象在第一、三象限. 2.如图所示的函数图象的关系式可能是( ) A.y=x B.y= C.y=x2 D.y= 设计意图:通过具体的习题使学生加深对本部分知识的理 解能解决具体问题。. B A 2 4 6 -2 -4 -6 4 -2 2 6 -4 -6 0 x y 即时反馈1、已知反比例函数的图像,如图, 请判断k是正数还是负数,如果 A(-3, y1)B(-1, y2 )是该图像上 的两点,那么y1与y2的大小关系 是怎样的? 目标归结: 1.画反比例函数的图象步骤. 2.反比例函数的性质. 3.反比例函数的图象在哪个象限由k决定,且y值随x值变化只能在“每一个象限内”研究. 4.在y=(k≠0)中,由于x≠0,同时y≠0,因此双曲线两个分支不可能到达坐标轴. 目标达成:【作业跟进】分层布置A B C 8 1.已知反比例函数y=的图象如图所示,则k > 0, 在图象的每一支上, y值随x的增大而 减小 . 2.下列图象中,是反比例函数的图象的是 (D) 3.在反比例函数y=(k<0)的图象上有两点A(x1,y1),B(x2,y2),且x1>x2>0,则y1-y2的值为 (A) (A)正数 (B)负数 (C)非正数 (D)非负数 4.已知反比例函数y=的图象在第一、三象限内,则k的值可是________(写出满足条件的一个k值即可). 5.在直角坐标系中,若一点的横坐标与纵坐标互为倒数,则这点一定在函数图象上 y= (填函数关系式). 6.若一次函数y=kx+b的图象经过第一、二、四象限,则反比例函数y=的图象一定在 二、四 象限. 7.两个不同的反比例函数的图象是否会相交?为什么? 8 【答案】 不会相交,因为当k1≠k2时,方程=无解. 8.点A(a,b)、B(a-1,c)均在反比例函数y=的图象上,若a<0,则b < c.【纠错补漏】 【教学反思】 8查看更多