2019-2020学年江西省抚州市八年级上学期期末数学试卷 （解析版）

2019-2020学年江西省抚州市八年级上学期期末数学试卷 （解析版）

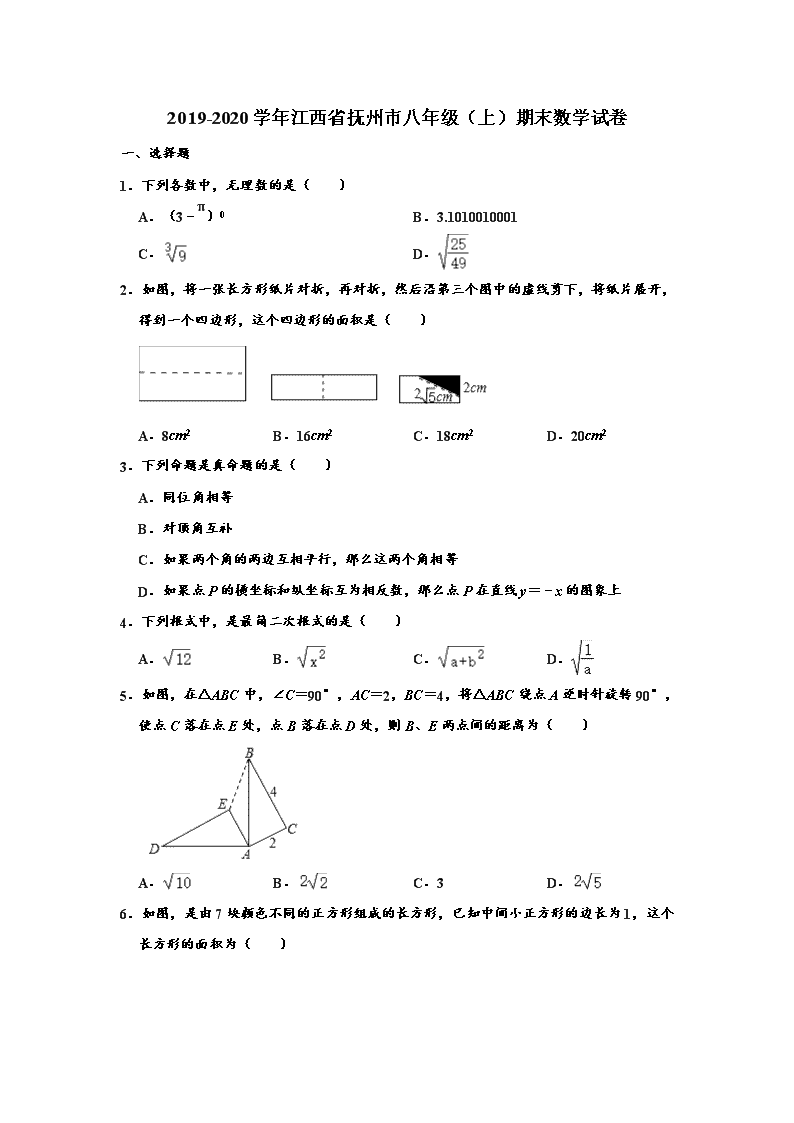
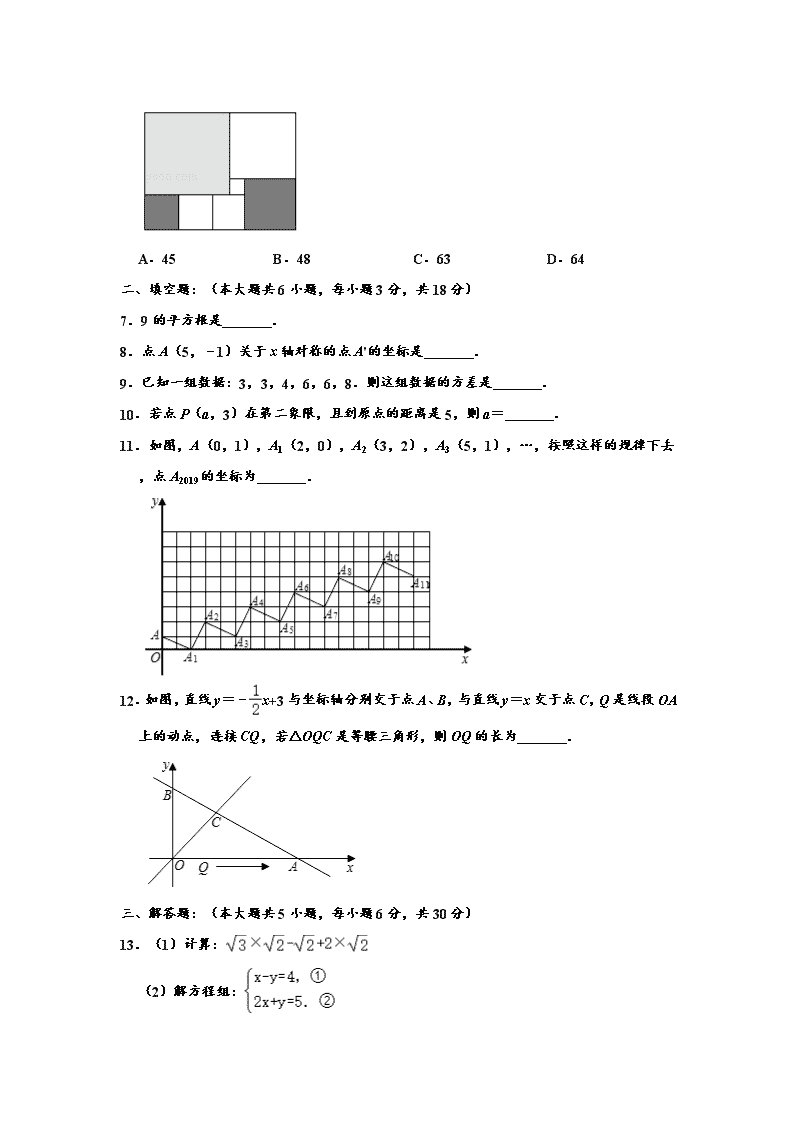
‎2019-2020学年江西省抚州市八年级（上）期末数学试卷 一、选择题 ‎1．下列各数中，无理数的是（　　）‎ A．（3﹣π）0 B．3.1010010001 ‎ C． D．‎ ‎2．如图，将一张长方形纸片对折，再对折，然后沿第三个图中的虚线剪下，将纸片展开，得到一个四边形，这个四边形的面积是（　　）‎ A．8cm2 B．16cm2 C．18cm2 D．20cm2‎ ‎3．下列命题是真命题的是（　　）‎ A．同位角相等 ‎ B．对顶角互补 ‎ C．如果两个角的两边互相平行，那么这两个角相等 ‎ D．如果点P的横坐标和纵坐标互为相反数，那么点P在直线y＝﹣x的图象上 ‎4．下列根式中，是最简二次根式的是（　　）‎ A． B． C． D．‎ ‎5．如图，在△ABC中，∠C＝90°，AC＝2，BC＝4，将△ABC绕点A逆时针旋转90°，使点C落在点E处，点B落在点D处，则B、E两点间的距离为（　　）‎ A． B． C．3 D．‎ ‎6．如图，是由7块颜色不同的正方形组成的长方形，已知中间小正方形的边长为1，这个长方形的面积为（　　）‎ A．45 B．48 C．63 D．64‎ 二、填空题：（本大题共6小题，每小题3分，共18分）‎ ‎7．9的平方根是　 　．‎ ‎8．点A（5，﹣1）关于x轴对称的点A'的坐标是　 　．‎ ‎9．已知一组数据：3，3，4，6，6，8．则这组数据的方差是　 　．‎ ‎10．若点P（a，3）在第二象限，且到原点的距离是5，则a＝　 　．‎ ‎11．如图，A（0，1），A1（2，0），A2（3，2），A3（5，1），…，按照这样的规律下去，点A2019的坐标为　 　．‎ ‎12．如图，直线y＝﹣x+3与坐标轴分别交于点A、B，与直线y＝x交于点C，Q是线段OA上的动点，连接CQ，若△OQC是等腰三角形，则OQ的长为　 　．‎ 三、解答题：（本大题共5小题，每小题6分，共30分）‎ ‎13．（1）计算：‎ ‎（2）解方程组：‎ ‎14．如图，直线CD、EF被直线l所截，∠DAB与∠ABF的角平分线相交于点G，且∠AGB＝90°，求证：CD∥EF．‎ ‎15．已知直线y＝kx+b经过点（3，3）和（﹣1，1），求该直线的解析式．‎ ‎16．用无刻度直尺作图并解答问题：‎ 如图，△ABD和△ACE都是等边三角形，在△ABC内部作一点P，使得∠BPC＝120°，并给予证明．‎ ‎17．如图，图中数字代表正方形的面积，∠ACB＝120°，求正方形P的面积．（提示：直角三角形中，30°角所对的直角边等于斜边的一半）‎ 四、解答题（本大题共3小题，每小题8分，共24分）‎ ‎18．现有甲乙丙三个厂家都生产一种灯泡，他们对外都宣称自己的灯泡使用寿命为12个月，为了检查他们灯泡的真正使用寿命，现随机从三个厂家均抽查11个灯泡进行检测，得到的数据如下：（单位：月）‎ 甲厂 ‎7‎ ‎8‎ ‎9‎ ‎9‎ ‎9‎ ‎11‎ ‎13‎ ‎14‎ ‎16‎ ‎17‎ ‎19‎ 乙厂 ‎7‎ ‎7‎ ‎9‎ ‎9‎ ‎10‎ ‎10‎ ‎12‎ ‎12‎ ‎12‎ ‎13‎ ‎14‎ 丙厂 ‎7‎ ‎7‎ ‎8‎ ‎8‎ ‎8‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎（1）这三个生产厂家分别利用了统计中的哪个特征数（平均数，众数，中位数）进行宣传；‎ ‎（2）如果三家灯泡售价相同，作为顾客，你会选择购买哪家的产品，请说明理由．‎ ‎19．父亲两次将100斤粮食分给兄弟俩，第一次分给哥哥的粮食等于第二次分给弟弟的2倍，第二次分给哥哥的粮食是第一次分给弟弟的3倍，求两次分粮食中，哥哥、弟弟各分到多少粮食？‎ ‎20．已知一次函数y＝kx+b（k≠0）的图象交x轴于点A（2，0），交y轴于点B，且△AOB的面积为3，求此一次函数的解析式．‎ 五、解答题：（本大题共2小题，每小题9分，共18分）‎ ‎21．如图，三角形ABC中，AC＝BC，D是BC上的一点，连接AD，DF平分∠ADC交∠ACB的外角∠ACE的平分线于F．‎ ‎（1）求证：CF∥AB；‎ ‎（2）若∠DAC＝40°，求∠DFC的度数．‎ ‎22．受气候的影响，某超市蔬菜供应紧张，需每天从外地调运蔬菜1000斤．超市决定从甲、乙两大型蔬菜棚调运蔬菜，已知甲蔬菜棚每天最多可调出800斤，乙蔬菜棚每天最多可调运600斤，从两蔬菜棚调运蔬菜到超市的路程和运费如表：‎ 到超市的路程（千米）‎ 运费（元/斤•千米）‎ 甲蔬菜棚 ‎120‎ ‎0.03‎ 乙蔬菜棚 ‎80‎ ‎0.05‎ ‎（1）若某天调运蔬菜的总运费为3840元，则从甲、乙两蔬菜棚各调运了多少斤蔬菜？‎ ‎（2）设从甲蔬菜棚调运蔬菜x斤，总运费为W元，试写出W与x的函数关系式，怎样安排调运方案才能使每天的总运费最省？‎ 六、（本大题共12分）‎ ‎23．如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A在x轴上，AB＝AC，∠BAC＝90°，且A（2，0）、B（3，3），BC交y轴于M，‎ ‎（1）求点C的坐标；‎ ‎（2）连接AM，求△AMB的面积；‎ ‎（3）在x轴上有一动点P，当PB+PM的值最小时，求此时P的坐标．‎ 参考答案 一、选择题：（本大题共6小题，每小题3分，共18分.每小题只有一个正确选项）‎ ‎1．下列各数中，无理数的是（　　）‎ A．（3﹣π）0 B．3.1010010001 ‎ C． D．‎ ‎【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．‎ 解：A．（3﹣π）0＝1，是整数，属于有理数；‎ B.3.1010010001是有限小数，属于有理数；‎ C.是无理数；‎ D.是分数，属于有理数．‎ 故选：C．‎ ‎2．如图，将一张长方形纸片对折，再对折，然后沿第三个图中的虚线剪下，将纸片展开，得到一个四边形，这个四边形的面积是（　　）‎ A．8cm2 B．16cm2 C．18cm2 D．20cm2‎ ‎【分析】直接利用折叠方法可得出展开的四边形是菱形，求出阴影部分面积进而得出答案．‎ 解：由题意可得：剪下来的三角形斜边为2cm，一直角边长为：2cm，‎ 故另一边长为：＝4（cm），‎ 故阴影部分面积为：×2×4＝4（cm2），‎ 则沿第三个图中的虚线剪下，将纸片展开，得到一个四边形，这个四边形的面积是：4×4＝16（cm2）．‎ 故选：B．‎ ‎3．下列命题是真命题的是（　　）‎ A．同位角相等 ‎ B．对顶角互补 ‎ C．如果两个角的两边互相平行，那么这两个角相等 ‎ D．如果点P的横坐标和纵坐标互为相反数，那么点P在直线y＝﹣x的图象上 ‎【分析】直接利用平行线的性质以及点的坐标特点、对顶角的性质分别分析得出答案．‎ 解：A、同位角相等，是假命题，不合题意；‎ B、对顶角相等，故原命题是假命题；‎ C、两个角的两边互相平行，‎ 如图（1）所示，∠1和∠2是相等关系，‎ 如图（2）所示，则∠3和∠4是互补关系，‎ ‎，‎ 故原命题是假命题；‎ D、如果点P的横坐标和纵坐标互为相反数，那么点P在直线y＝﹣x的图象上，是真命题．‎ 故选：D．‎ ‎4．下列根式中，是最简二次根式的是（　　）‎ A． B． C． D．‎ ‎【分析】根据最简二次根式的定义逐个判断即可．‎ 解：A、＝2不是最简二次根式，故本选项不符合题意；‎ B、＝|x|，不是最简二次根式，故本选项不符合题意；‎ C、不能化简，是最简二次根式，故本选项符合题意；‎ D、＝，不是最简二次根式，故本选项不符合题意；‎ 故选：C．‎ ‎5．如图，在△ABC中，∠C＝90°，AC＝2，BC＝4，将△ABC绕点A逆时针旋转90°‎ ‎，使点C落在点E处，点B落在点D处，则B、E两点间的距离为（　　）‎ A． B． C．3 D．‎ ‎【分析】延长DE交BC于F，由旋转的性质可得AE＝AC＝2，∠EAC＝90°＝∠DEA＝∠ACB，可得AE∥CB，AC∥EF，由平行线间的平行线段相等，可得CF＝EF＝2＝AC，∠EFC＝90°，由勾股定理可求解．‎ 解：如图，延长DE交BC于F，‎ ‎∵将△ABC绕点A逆时针旋转90°，‎ ‎∴AE＝AC＝2，∠EAC＝90°＝∠DEA＝∠ACB，‎ ‎∴AE∥CB，AC∥EF，‎ ‎∴CF＝EF＝2＝AC，∠EFC＝90°，‎ ‎∴BF＝2，‎ ‎∴BE＝＝＝2，‎ 故选：B．‎ ‎6．如图，是由7块颜色不同的正方形组成的长方形，已知中间小正方形的边长为1，这个长方形的面积为（　　）‎ A．45 B．48 C．63 D．64‎ ‎【分析】设左下角的小正方形边长为x，左上角最大的正方形的边长为y ‎，根据矩形的长和宽列出方程组求解即可．‎ 解：设左下角的小正方形边长为x，左上角最大的正方形的边长为y，‎ 根据题意得：，‎ 解得，‎ 矩形的长＝2+2+2+3＝9，‎ 宽＝2+5＝7，‎ 面积＝7×9＝63．‎ 故选：C．‎ 二、填空题：（本大题共6小题，每小题3分，共18分）‎ ‎7．9的平方根是　±3　．‎ ‎【分析】直接利用平方根的定义计算即可．‎ 解：∵±3的平方是9，‎ ‎∴9的平方根是±3．‎ 故答案为：±3．‎ ‎8．点A（5，﹣1）关于x轴对称的点A'的坐标是　（5，1）　．‎ ‎【分析】根据关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数可得答案．‎ 解：点A（5，﹣1）关于x轴对称的点A'的坐标是（5，1）．‎ 故答案为：（5，1）．‎ ‎9．已知一组数据：3，3，4，6，6，8．则这组数据的方差是　　．‎ ‎【分析】利用方差的意义求解．‎ 解：（3+3+4+6+6+8）÷6＝5，‎ ‎×[（3﹣5）2+（3﹣5）2+（4﹣5）2+（6﹣5）2+（6﹣5）2+（8﹣5）2]‎ ‎＝×（4+4+1+1+1+9）‎ ‎＝．‎ 则这组数据的方差是．‎ 故答案为：．‎ ‎10．若点P（a，3）在第二象限，且到原点的距离是5，则a＝　﹣4　．‎ ‎【分析】由a2+32＝52即可求出a的值．‎ 解：∵点P到原点的距离是5，‎ ‎∴a2+32＝52．‎ ‎∴a＝±4．‎ ‎∵点P（a，3）在第二象限，‎ ‎∴a＝﹣4．‎ 故答案为：﹣4．‎ ‎11．如图，A（0，1），A1（2，0），A2（3，2），A3（5，1），…，按照这样的规律下去，点A2019的坐标为　（3029，1009）　．‎ ‎【分析】观察图形得到奇数点的规律为，A1（2，0），A3（5，1），A5（8，2），…，A2n﹣1（3n﹣1，n﹣1），由2019是奇数，且2019＝2n﹣1，则可求A2n﹣1（3029，1009）．‎ 解：观察图形可得，A1（2，0），A3（5，1），A5（8，2），…，A2n﹣1（3n﹣1，n﹣1），‎ A2（3，2），A4（6，3），A6（9，4），…，A2n（3n，n+1），‎ ‎∵2019是奇数，且2019＝2n﹣1，‎ ‎∴n＝1010，‎ ‎∴A2n﹣1（3029，1009），‎ 故答案为（3029，1009）．‎ ‎12．如图，直线y＝﹣x+3与坐标轴分别交于点A、B，与直线y＝x交于点C，Q是线段OA上的动点，连接CQ，若△OQC是等腰三角形，则OQ的长为　2或4或2　．‎ ‎【分析】分别求出A（6，0），C（2，2），则可求OC＝2；分三种情况求：①当OC＝CQ时，OQ的中点横坐标是；②当OC＝OQ时，OQ＝2；③当OQ＝CQ时，设Q（x，0），x2＝（x﹣2）2+4，OQ＝2．‎ 解：令y＝0，可得﹣x+3＝0，‎ ‎∴x＝6，‎ ‎∴A（6，0），‎ 令x＝﹣x+3，解得x＝2，‎ ‎∴C（2，2），‎ ‎∴OC＝2，‎ ‎∵△OQC是等腰三角形，‎ ‎①当OC＝CQ时，OQ的中点横坐标是2，‎ ‎∴OQ＝4；‎ ‎②当OC＝OQ时，OQ＝2，‎ ‎∴OQ＝2；‎ ‎③当OQ＝CQ时，‎ 设Q（x，0），‎ ‎∴x2＝（x﹣2）2+4，‎ ‎∴x＝2，‎ ‎∴OQ＝2；‎ 故答案为2或4或2．‎ 三、解答题：（本大题共5小题，每小题6分，共30分）‎ ‎13．（1）计算：‎ ‎（2）解方程组：‎ ‎【分析】（1）先进行二次根式的乘法运算，然后合并即可；‎ ‎（2）利用加减消元法解方程组．‎ 解：（1）原式＝﹣+2‎ ‎＝+；‎ ‎（2）由①+②得3x＝9，‎ 解得x＝3，‎ 把x＝3代入①得y＝﹣1，‎ 所以原方程组的解是．‎ ‎14．如图，直线CD、EF被直线l所截，∠DAB与∠ABF的角平分线相交于点G，且∠AGB＝90°，求证：CD∥EF．‎ ‎【分析】根据三角形内角和定理可得∠BAG+∠ABG＝90°，再根据角平分线的定义得到∠BAD+∠ABF＝180°，再根据平行线的判定即可求解．‎ ‎【解答】证明：∵∠AGB＝90°，‎ ‎∴∠BAG+∠ABG＝90°，‎ ‎∵AG平分∠BAD，‎ ‎∴∠BAD＝2∠BAG，‎ ‎∵BG平分∠ABF，‎ ‎∴∠ABF＝2∠ABG，‎ ‎∴∠BAD+∠ABF＝2∠BAG+2∠ABG＝180°，‎ ‎∴CD∥EF．‎ ‎15．已知直线y＝kx+b经过点（3，3）和（﹣1，1），求该直线的解析式．‎ ‎【分析】根据直线y＝kx+b经过两点（3，3）和（﹣1，1），利用待定系数法列式求出k、b的值，从而得解．‎ 解：设该直线的解析式为y＝kx+b，‎ 把（3，3），（﹣1，1）代入得：，‎ 解得 ‎∴该直线的解析式为．‎ ‎16．用无刻度直尺作图并解答问题：‎ 如图，△ABD和△ACE都是等边三角形，在△ABC内部作一点P，使得∠BPC＝120°，并给予证明．‎ ‎【分析】连接CD、BE交于点P，∠BPC＝120°．根据△ABD和△ACE都是等边三角形，证明△DAC≌△BAE，进而证明∠BPD＝∠DAB＝60°，∠BPC＝120°．‎ 解：如图，‎ 点P即为所求．‎ 解：如图，连接CD、BE交于点P，∠BPC＝120°．‎ 证明：∵△ABD和△ACE都是等边三角形，‎ ‎∴AD＝AB、AC＝AE，∠DAB＝∠EAC＝60°，‎ ‎∴∠DAB+∠BAC＝∠EAC+∠BAC，‎ 即∠DAC＝∠BAE；‎ ‎∴△DAC≌△BAE（SAS），‎ ‎∴∠ADC＝∠ABE，‎ 又∠AQD＝∠BQP ‎∴∠BPD＝∠DAB＝60°，‎ ‎∴∠BPC＝120°．‎ ‎17．如图，图中数字代表正方形的面积，∠ACB＝120°，求正方形P 的面积．（提示：直角三角形中，30°角所对的直角边等于斜边的一半）‎ ‎【分析】作AD⊥BC，交BC延长线于D，求出CD＝AC＝1，AD＝，根据勾股定理可求出AB，则答案可得出．‎ 解：如图，作AD⊥BC，交BC延长线于D，‎ ‎∵∠ACB＝120°，‎ ‎∴∠ACD＝60°，∠DAC＝30°；‎ ‎∴CD＝AC＝1，‎ ‎∴AD＝，‎ 在直角三角形ADB中，BD＝BC+CD＝3+1＝4，AD＝，‎ 根据勾股定理得：AB2＝AD2+BD2＝3+16＝19；‎ ‎∴正方形P的面积＝AB2＝19．‎ 四、解答题（本大题共3小题，每小题8分，共24分）‎ ‎18．现有甲乙丙三个厂家都生产一种灯泡，他们对外都宣称自己的灯泡使用寿命为12个月，为了检查他们灯泡的真正使用寿命，现随机从三个厂家均抽查11个灯泡进行检测，得到的数据如下：（单位：月）‎ 甲厂 ‎7‎ ‎8‎ ‎9‎ ‎9‎ ‎9‎ ‎11‎ ‎13‎ ‎14‎ ‎16‎ ‎17‎ ‎19‎ 乙厂 ‎7‎ ‎7‎ ‎9‎ ‎9‎ ‎10‎ ‎10‎ ‎12‎ ‎12‎ ‎12‎ ‎13‎ ‎14‎ 丙厂 ‎7‎ ‎7‎ ‎8‎ ‎8‎ ‎8‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎（1）这三个生产厂家分别利用了统计中的哪个特征数（平均数，众数，中位数）进行宣传；‎ ‎（2）如果三家灯泡售价相同，作为顾客，你会选择购买哪家的产品，请说明理由．‎ ‎【分析】（1）根据平均数，众数，中位数的定义判断即可．‎ ‎（2）根据平均数，中位数的值判断即可．‎ 解：（1）∵甲厂的平均数＝12，乙厂的众数为12，丙厂的中位数为12，‎ ‎∴甲厂用了统计中的平均数、乙厂用了统计中的众数、丙厂用了统计中的中位数进行宣传．‎ ‎（2）选用甲厂的产品，因为平均数较真实地反映了灯泡的使用寿命；‎ ‎（或选用丙厂的产品，因为丙厂有一半以上的灯泡使用寿命不少于12个月；）．‎ ‎，‎ ‎19．父亲两次将100斤粮食分给兄弟俩，第一次分给哥哥的粮食等于第二次分给弟弟的2倍，第二次分给哥哥的粮食是第一次分给弟弟的3倍，求两次分粮食中，哥哥、弟弟各分到多少粮食？‎ ‎【分析】根据“第一次分给哥哥的粮食等于第二次分给弟弟的2倍，第二次分给哥哥的粮食是第一次分给弟弟的3倍”两个等量关系列出方程组求得答案即可．‎ 解：设哥哥第一次分到粮食为x斤，弟弟第二次分到的粮食为y斤，依题意得：，‎ 解得，‎ 第一次弟弟：100﹣80＝20（斤），‎ 第二次哥哥：100﹣40＝60（斤），‎ 答：第一次，哥哥分到80斤，弟弟分到20斤，第二次，哥哥分到60斤，弟弟分到40斤．‎ ‎20．已知一次函数y＝kx+b（k≠0）的图象交x轴于点A（2，0），交y轴于点B，且△AOB的面积为3，求此一次函数的解析式．‎ ‎【分析】根据三角形的面积求出B点坐标为（0，3）或（0，﹣3），然后利用待定系数法求解即可．‎ 解：∵A（2，0），S△AOB＝3，‎ ‎∴OB＝3，‎ ‎∴B（0，3）或（0，﹣3）．‎ ‎①当B（0，3）时，把A（2，0）、B（0，3）代入y＝kx+b中得 ‎∴，‎ 解得：．‎ ‎∴一次函数的解析式为．‎ ‎②当B（0，﹣3）时，把A（2，0）、B（0，﹣3）代入y＝kx+b中得，‎ ‎，‎ 解得：．‎ ‎∴．‎ 综上所述，该函数解析式为y＝﹣x+3或y＝x﹣3．‎ 五、解答题：（本大题共2小题，每小题9分，共18分）‎ ‎21．如图，三角形ABC中，AC＝BC，D是BC上的一点，连接AD，DF平分∠ADC交∠ACB的外角∠ACE的平分线于F．‎ ‎（1）求证：CF∥AB；‎ ‎（2）若∠DAC＝40°，求∠DFC的度数．‎ ‎【分析】（1）根据三角形的性质得到∠B＝∠BAC，由三角形外角的性质得到∠ACE＝∠B+∠BAC，求得∠BAC＝，由角平分线的定义得到∠ACF＝∠ECF＝，等量代换得到∠BAC＝∠ACF，根据平行线的判定定理即可得到结论；‎ ‎（2）根据角平分线的定义和三角形的内角和即可得到结论．‎ ‎【解答】（1）证明：∵AC＝BC，‎ ‎∴∠ABC＝∠CAB，‎ ‎∴∠ACE＝∠ABC+∠CAB＝2∠ABC ‎∵CF是∠ACE的平分线，‎ ‎∴∠ACE＝2∠FCE ‎∴2∠ABC＝2∠FCE，‎ ‎∴∠ABC＝∠FCE，‎ ‎∴CF∥AB；‎ ‎（2）∵CF是∠ACE的平分线，‎ ‎∴∠ACE＝2∠FCE＝∠ADC+∠DAC ‎∵DF平分∠ADC，‎ ‎∴∠ADC＝2∠FDC；‎ ‎∴2∠FCE＝∠ADC+∠DAC＝2∠FDC+∠DAC，‎ ‎∴2∠FCE﹣2∠FDC＝∠DAC ‎∵∠DFC＝∠FCE﹣∠FDC ‎∴2∠DFC＝2∠FCE﹣2∠FDC＝∠DAC＝40°‎ ‎∴∠DFC＝20°．‎ ‎22．受气候的影响，某超市蔬菜供应紧张，需每天从外地调运蔬菜1000斤．超市决定从甲、乙两大型蔬菜棚调运蔬菜，已知甲蔬菜棚每天最多可调出800斤，乙蔬菜棚每天最多可调运600斤，从两蔬菜棚调运蔬菜到超市的路程和运费如表：‎ 到超市的路程（千米）‎ 运费（元/斤•千米）‎ 甲蔬菜棚 ‎120‎ ‎0.03‎ 乙蔬菜棚 ‎80‎ ‎0.05‎ ‎（1）若某天调运蔬菜的总运费为3840元，则从甲、乙两蔬菜棚各调运了多少斤蔬菜？‎ ‎（2）设从甲蔬菜棚调运蔬菜x斤，总运费为W元，试写出W与x的函数关系式，怎样安排调运方案才能使每天的总运费最省？‎ ‎【分析】（1）设从甲蔬菜棚调运蔬菜x斤，则从乙蔬菜棚调运蔬菜（1000﹣x）斤，根据题意列方程解答即可；‎ ‎（2 ）根据题意写出W与x的关系式以及x的取值范围，再根据一次函数的性质解答即可．‎ 解：（1）设从甲蔬菜棚调运蔬菜x斤，则从乙蔬菜棚调运蔬菜（1000﹣x）斤，得 ‎120×0.03x+80×0.05×（1000﹣x）＝3840，‎ 解得x＝400，‎ 乙蔬菜棚调运蔬菜：1000﹣400＝600（斤），‎ 答：从甲蔬菜棚调运了400斤、从乙蔬菜棚调运了600斤蔬菜；‎ ‎（2）W＝120×0.03x+80×0.05×（1000﹣x），‎ 即W＝﹣0.4x+4000（400≤x≤800），‎ ‎∵﹣0.4＜0，‎ ‎∴W随x的增大而减小，‎ 当x＝800时，W最小，W最小值＝3680（元），‎ 答：从甲蔬菜棚调运蔬菜800斤，从乙蔬菜棚调运蔬菜200斤总费用最省．‎ 六、（本大题共12分）‎ ‎23．如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A在x轴上，AB＝AC，∠BAC＝90°，且A（2，0）、B（3，3），BC交y轴于M，‎ ‎（1）求点C的坐标；‎ ‎（2）连接AM，求△AMB的面积；‎ ‎（3）在x轴上有一动点P，当PB+PM的值最小时，求此时P的坐标．‎ ‎【分析】（1）作CD⊥x轴于D，BE⊥x轴于E，证明△CDA≌△AEB，根据全等三角形的性质得到CD＝AE，AD＝BE，求出点C的坐标；‎ ‎（2）利用待定系数法求出直线BC的解析式，得到OM的长，根据梯形的面积公式、三角形的面积公式计算，得到答案；‎ ‎（3）根据轴对称﹣最短路径问题作出点P，求出直线BM′的解析式，根据x轴上点的坐标特征求出点P的坐标．‎ 解：（1）如图1，作CD⊥x轴于D，BE⊥x轴于E，‎ ‎∴∠CAD+∠DCA＝90°，‎ ‎∵∠BAC＝90°，‎ ‎∴∠CAD+∠BAE＝90°，‎ ‎∴∠BAE＝∠ACD，‎ 在△CDA和△AEB中，‎ ‎，‎ ‎∴△CDA≌△AEB（AAS），‎ ‎∴CD＝AE，AD＝BE，‎ ‎∵A（2，0）、B（3，3），‎ ‎∴OA＝2，OE＝BE＝3，‎ ‎∴CD＝AE＝1，OD＝AD﹣OA＝1，‎ ‎∴C的坐标是（﹣1，1）；‎ ‎（2）如图2，作BE⊥x轴于E，‎ 设直线BC的解析式为y＝kx+b，‎ ‎∵B点的坐标为（3，3），C点的坐标是（﹣1，1），‎ ‎∴，‎ 解得，，‎ ‎∴直线BC的解析式为y＝x+，‎ 当x＝0时，y＝，‎ ‎∴OM＝，‎ ‎∴△AMB的面积＝梯形MOEB的面积﹣△AOM的面积﹣△AEB的面积 ‎＝×（+3）×3﹣×2×﹣×1×3‎ ‎＝；‎ ‎（3）如图3，作M关于x轴的对称点M′（0，﹣），连接BM'，交x轴于点P，此时PB+PM的值最小，‎ 设直线BM′的解析式为y＝mx+n，‎ 则，‎ 解得，，‎ ‎∴直线BM′的解析式为y＝x﹣，‎ 点P在x轴上，当x＝0时，y＝1，‎ ‎∴点P的坐标为（1，0）．‎