- 2021-04-27 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江中考数学专题训练——解答题3
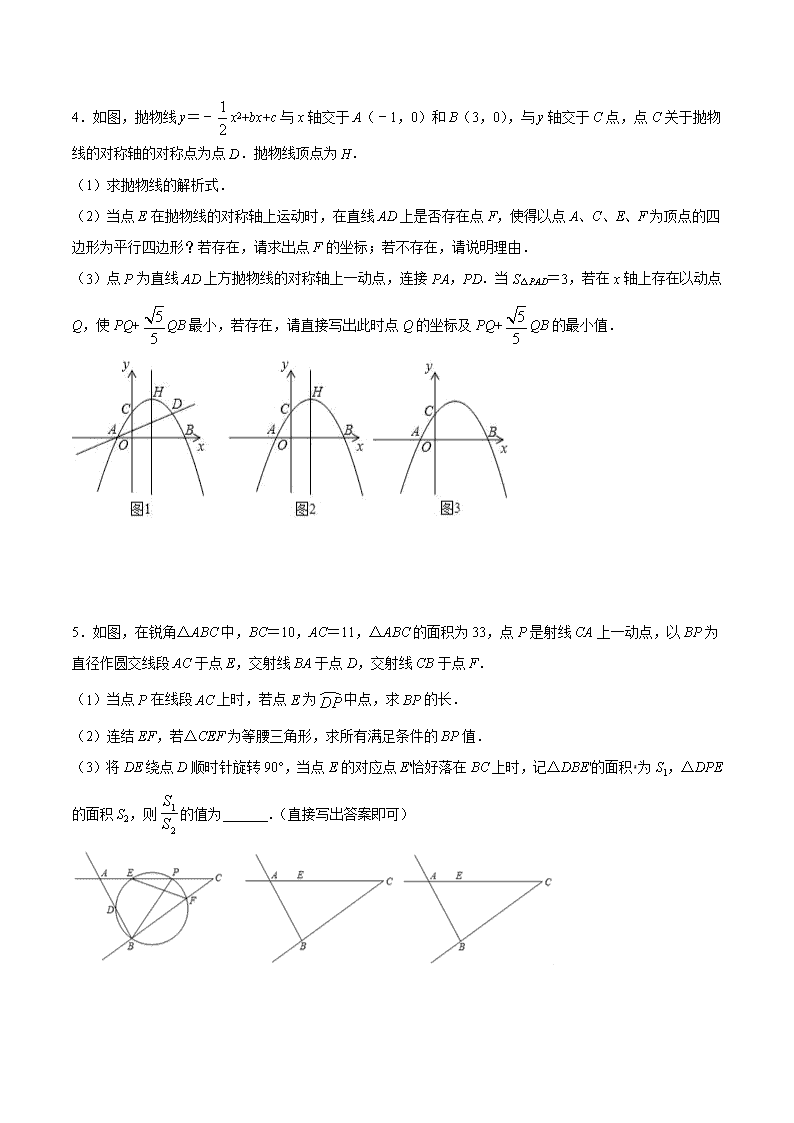
浙江中考数学专题训练——解答题3 1.(1)计算:2sin30°+(2﹣π)0﹣; (2)解方程:2x2+x﹣6=0. 2.先化简,再求值:,其中a =-1. 3.如图,已知△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,且DE=DF.试说明AB=AC的理由. 4.如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)和B(3,0),与y轴交于C点,点C关于抛物线的对称轴的对称点为点D.抛物线顶点为H. (1)求抛物线的解析式. (2)当点E在抛物线的对称轴上运动时,在直线AD上是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由. (3)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在以动点Q,使PQ+QB最小,若存在,请直接写出此时点Q的坐标及PQ+QB的最小值. 5.如图,在锐角△ABC中,BC=10,AC=11,△ABC的面积为33,点P是射线CA上一动点,以BP为直径作圆交线段AC于点E,交射线BA于点D,交射线CB于点F. (1)当点P在线段AC上时,若点E为中点,求BP的长. (2)连结EF,若△CEF为等腰三角形,求所有满足条件的BP值. (3)将DE绕点D顺时针旋转90°,当点E的对应点E'恰好落在BC上时,记△DBE'的面积为S1,△DPE的面积S2,则的值为 .(直接写出答案即可) 6.如图,在 Rt△AOB 中,∠AOB=90°,OA=3,OB=4,线段 OA’绕点 O 顺时针旋转ɑ角(0≤ɑ≤180°),OA’交边 AB 于点 F. (1)当旋转ɑ角度后,A’点恰好落在 AB 上,记为 C 点,求 CB 的长度; (2)当 OA’绕点 O 旋转与 AB 平行时,记为 OG,连接 CG,交 OB 于 E,分别求出 OE 长度和∠COB 的正弦值; (3)在旋转过程中,请直接写出的最大值. 7.已知二次函数 y=(x-a-2)(x+a)+3. (1)求该二次函数的图象的对称轴. (2)对于该二次函数图象上的两点 P(x1,y1)、Q(x2,y2). ①当 x≥m 时,y 随 x 的增大而增大,写出一个符合条件的 m 值; ②当 m≤x2≤m+2,当 x1≤﹣1 时,均有 y1≥y2,求 m 的取值范围; (3)当二次函数过(0,3)点时,且与直线 y=kx+2 交于 A、B 两点,其中有一交点的横坐标 x0 满足 1<x0<3, 求 k 的取值范围. 8.如图 1,在矩形 ABCD 中,点 E 以 lcm/s 的速度从点 A 向点 D 运动,运动时间为 t(s),连结 BE,过点 E 作 EF⊥BE,交 CD 于 F,以 EF 为直径作⊙O. (1)求证:∠1=∠2; (2)如图 2,连结 BF,交⊙O 于点 G,并连结 EG.已知 AB=4,AD=6. ①用含 t 的代数式表示 DF 的长 ②连结 DG,若△EGD 是以 EG 为腰的等腰三角形,求 t 的值; (3)连结 OC,当 tan∠BFC=3 时,恰有 OC∥EG,请直接写出 tan∠ABE 的值. 9.如图,在锐角△ABC中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线DE交边BC于点E,连结BD. (1)求证:∠ABD=∠CDE. (2)若AC=28,tanA=2,AD:DC=1:3,求DE的长. 10.如图,直角坐标系中,抛物线y=a(x﹣4)2﹣16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y=x+b分别交x,y轴于点A,B. (1)写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示). (2)若AF=AH=OH,求证:∠CEO=∠ABO. (3)当b>﹣4时,以AB为边作正方形,使正方形的另外两个顶点一个落在抛物线上,一个落在抛物线的对称轴上,求所有满足条件的a及相应b的值.(直接写出答案即可) 参考答案 1.(1)-1;(2)x1=,x2=﹣2. 【解析】 【分析】 (1)根据三角形函数中30°的正弦值为,任何一个数的零指数幂(0除外)是1,有理数的负指数幂是它正指数幂的倒数即可求解. (2)利用因式分解中“十字相乘法”即可把一元二次方程分解为(2x-3)(x+2)=0即可求解. 【详解】 解:(1)原式=2×+1﹣3 =1+1﹣3 =﹣1; (2)(2x﹣3)(x+2)=0, 2x﹣3=0或x+2=0, 所以x1=,x2=﹣2. 【点睛】 本题主要考查的是实数的综合应用和一元二次方程解法“十字相乘法”,掌握这个两个知识点是解题的关键. 2.,. 【解析】 【分析】 先根据混合运算的法则把原分式化为最简形式,再把a=-1代入进行计算即可. 【详解】 解:原式== 当a =-1时,原式=. 3.见解析 【解析】 【分析】 因DE⊥AB于E,DF⊥AC于F,D是BC的中点,所以Rt△DBE≌Rt△DCF,根据全等三角形的性质可知∠B=∠C,则AB=AC. 【详解】 解:∵DE⊥AB,DF⊥AC, ∴△DBE与△DCF是直角三角形. ∵在Rt△DBE与Rt△DCF中, , ∴Rt△DBE≌Rt△DCF(HL), ∴∠B=∠C, ∴AB=AC. 【点睛】 本题考查的是全等三角形的判定、等腰三角形的判定,判定两个三角形是全等三角形有以下方法:ASA、AAS、SAS、SSS、HL. 4.(1)(2)(0,)或(2,)或(﹣2,﹣)(3)(2.5,0) 【解析】 【分析】 (1)把A(﹣1,0)和B(3,0),代入到抛物线的解析式,即可解答 (2)存在,分三种情况讨论,①EF可由AC平移得到,C、E为对应点,A、F为对应点,再把F点代入直线AD的解析式为y=x+,即可解答②如图2所示,此时点F与点D重合,即可解答③如图3所示,根据平移的规律,得知点F的横坐标为﹣2, 代入解析式即可解答 (3)如图4所示,过点B作AD的平行线交抛物线的对称轴于点N,过点P作PH垂直于BN,与x轴的交点即为点Q,设直线BN的解析式为y=x+b,过点B(3,0),求出BN的解析式,再利用解析式算出M,N的值,再算出PQ+QB=PQ+QH,当P、Q、H三点共线时,PQ+QB最小,即为PH,即可解答 【详解】 (1)∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)和B(3,0), ∴, 解得,, ∴抛物线的解析式为:; (2)存在,分三种情况讨论, ①如图1所示, ∵四边形ACEF为平行四边形, ∴EF可由AC平移得到,C、E为对应点,A、F为对应点, ∵C(0,),点E的横坐标为1, ∴向右平移了一个单位, ∵A(﹣1,0), ∴F的横坐标为0, ∵直线AD的解析式为y=x+, ∴当x=0时,y=, ∴F(0,). ②如图2所示, 此时点F与点D重合, ∴F(2,). ③如图3所示, 根据平移的规律,得知点F的横坐标为﹣2, 当x=﹣2时,y=﹣, ∴F(﹣2,﹣). 综上所述:点F的坐标为(0,)或(2,)或(﹣2,﹣). (3)如图4所示,过点B作AD的平行线交抛物线的对称轴于点N,过点P作PH垂直于BN,与x轴的交点即为点Q, 设直线BN的解析式为y=x+b,过点B(3,0), 解得b=﹣, ∴直线BN的解析式为y=x﹣, ∵抛物线的对称轴为直线x=1, ∴N(1,﹣1), 设直线AD与抛物线的对称轴的交点为点M, ∴M(1,1), ∵S△ADP=PM•(xD﹣xA)•=3, ∴PM=2, ∴P(1,3), ∵tan∠ABN=, ∴QB=QH, ∴PQ+QB=PQ+QH, ∴当P、Q、H三点共线时,PQ+QB最小,即为PH, ∵PN=4,∠NPH=∠ABN, ∴PH=. ∴PQ+QB的最小值为, 此时点Q(2.5,0). 【点睛】 此题为抛物线的综合题,利用了轴对称性质,三角函数值,平行四边形的性质,解题关键在于把已知点代入解析式 5.(1);(2)或10或2;(3). 【解析】 【分析】 (1)先利用面积求高BE,再由勾股定理求AB、AE、CE,再根据全等三角形判定和性质求得PB; (2)△CEF为等腰三角形,可以分三种情况:①CF=EF,过F作FG⊥AC于点G,连接PF,利用相似三角形性质即可得到答案;②EF=CE,过E作EG⊥CB于G,连接EF、BP,利用全等三角形判定和性质即可;③CE=CF,利用全等三角形判定、性质和勾股定理即可; (3)过点E作EM⊥DP于点M,过E′作E′G⊥AC于点G,作E′N⊥AB于点N,过D作DF⊥AC于点F,作DH⊥E′G于点H,依次证明:DFGH是矩形,△DEF≌△DE′H(AAS),△E′DN≌△EDM(AAS),再运用由相似三角形性质和解直角三角形知识即可. 【详解】 解:(1)如图1,连接BE、DE,∴BP为直径, ∴∠BEC=∠BEA=90° ∵BC=10,AC=11,△ABC的面积为33, ∴AC•BE=33 ∴BE=6 ∴CE==8 ∴AE=AC﹣CE=3 ∴AB==3 ∵点E为中点 ∴∠ABE=∠PBE ∵BE=BE ∴△ABE≌△PBE(ASA) ∴BP=AB=3; (2)∵△CEF为等腰三角形,可以分三种情况: ①CF=EF,如图2,过F作FG⊥AC于点G,连接PF, ∵BP是直径 ∴∠BFP=∠CFP=∠CGF=∠CEB=90° ∴EG=CG=CF=4 ∵FG∥BE ∴△CFG∽△CBE∽△CPF ∴==,= ∴,即CF=5, ∴=,即CP=, ∴EP=CE﹣CP=8﹣=, ∴BP===; ②EF=CE,如图3,过E作EG⊥CB于G,连接EF、BP,则CG=GF ∴∠EFG=∠C ∵= ∴∠BPE=∠EFG ∴∠C=∠BPE ∵∠CEB=∠PEB=90°,BE=BE ∴△CBE≌△PBE(AAS) ∴BP=BC=10 ③CE=CF,如图4,连接EF、BP、BE、AF, ∵BP为直径 ∴∠AFB=∠AEB=90° ∵∠C=∠C ∴△CEB≌△CFP(ASA) ∴CP=CB=10 ∴PE=2 ∴BP===2 综上所述,满足条件的BP值为:或10或. (3)如图5,过点E作EM⊥DP于点M,过E′作E′G⊥AC于点G,作E′N⊥AB于点N,过D作DF⊥AC于点F,作DH⊥E′G于点H, ∵DF⊥AC,DH⊥E′G,E′G⊥AC ∴∠DFE=∠DHE′=∠E′GF=90° ∴DFGH是矩形, ∴GH=DF FG=DH∠FDH=90° ∴∠EDF+∠EDH=90° ∵∠EDH+∠E′DH=90° ∴∠EDF=∠E′DH ∵DE=DE′ ∴△DEF≌△DE′H(AAS) ∴DF=DH,EF=E′H ∵DF∥BE ∴==,设AF=m,则:DF=DH=GH=FG=2m,EF=E′H=3﹣m, ∴E′G=m+3,AG=3m,CG=CA﹣AG=11﹣3m, ∵tan∠C====,即:4E′G=3CG, ∴4(m+3)=3(11﹣3m),解得:m=, EF=3﹣=,DF=2×=, ∵BP是直径, ∴∠E′DN+∠E′DP=90°, ∵∠E′DP+∠EDM=90° ∴∠E′DN=∠EDM ∴△E′DN≌△EDM(AAS) ∴E′N=EM ∴===tan∠BPD ∵ ∴∠BED=∠BPD ∵DF∥BE ∴∠BED=∠EDF ∴∠BPD=∠EDF ∴tan∠BPD=tan∠EDF== ∴=, 故答案为:. 【点睛】 本题考查了圆的性质、相似三角形判定和性质、全等三角形判定和性质、勾股定理、解直角三角形、三角形面积等,涉及知识点较多,难度较大,特别是第(3)问要合理添辅助线构造全等三角形和相似三角形. 6.(1)CB=;(2)OE=,;(3) 【解析】 【分析】 (1) 过O作AB的垂线交AB于D,根据面积法求出AD,从而可求出CB; (2)平行得△CEB△OEG, 过C作CH⊥OB,可求长度和∠的正弦值; (3)由图像易知当OA'⊥AB时,FO最短,此时取得最大值为 【详解】 解:(1) 过O作AB的垂线交AB于D, ∵, ∴OD=, ∴AD=CD=, CB=; (2)∵OG∥AB, ∴∠B=∠BOG, ∵∠BEC=∠OEG, ∴以△CEB∽△GEO, ∴, ∴BE=, ∵OB=EB+EO=4, ∴OE+=4, 解得OE=, 过C作CH⊥OB,则△BCH∽△BAO, ∴=, ∴CH=, ∴; (3)由图像易知当OA'⊥AB时,FO最短,此时取得最大值为. 【点睛】 本题考查了旋转的性质,勾股定理,垂线段最短,以及相似三角形的判断与性质. 熟练掌握相似三角形的判定与性质是解答本题的关键. 7.(1)x=1;(2)①m值可以为2;②-1≤m≤1;(3) 【解析】 【分析】 (1)首先把原二次函数化成y=(x-1)2-a2-2a+2,由此可得该二次函数的图象的对称轴; (2)①根据二次函数的开口方向和对称轴可知y随x的增大而增大时,x的取值范围,从而可得符合条件的m值; ②首先得出当x1=-1,y1=y2时,x2=3,然后根据当x1≤-1时,均有y1≥y2,可得一个不等式组,解出即可; (3)首先根据二次函数过(0,3)点,求出a的值,于是可得该二次函数的解析式,然后计算出直线x=1,直线x=3与二次函数y=x2-2x+3的交点坐标,得到直线DE的解析式为y=2,k1=0,设DF所在直线解析式为y=k2x+2,把(3,6)代入得k2=即可得出结论. 【详解】 解:(1)因为y=(x-a-2)(x+a)+3, ∴y=(x-1)2-a2-2a+2, ∴该二次函数的图象的对称轴为x=1; (2)①∵该二次函数开口向上,对称轴为x=1, ∴x≥1时,y随x的增大而增大, ∴m≥1的数都可以, 因此符合条件的m值可以为2; ②∵该二次函数的图象的对称轴为x=1, ∴当x1=-1,y1=y2时,x2=3, ∴当x1≤-1时,均有y1≥y2, 则-1≤x2≤3, ∴, 解得-1≤m≤1; (3)当二次函数过(0,3)点时, 则有3=(0-1)2-a2-2a+2, 解得a=0或-2, ∴该二次函数的解析式为y=x2-2x+3, 如图: 直线x=1,直线x=3分别与二次函数y=x2-2x+3交E、F两点, 易得E(1,2),F(3,6), 直线y=kx+2与y轴交于D点,D(0,2), ∵二次函数y=x2-2x+3与直线y=kx+2交于A、B两点,其中有一交点的横坐标满足1<x0<3, 直线y=kx+2与二次函数y=x2-2x+3的EF间有一交点, 直线DE的解析式为y=2,k1=0,设DF所在直线的解析式为y=k2x+2,把(3,6)代入得k2=, ∴k1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档