【物理】2020届一轮复习人教版 牛顿运动定律的综合应用 课时作业
2020届一轮复习人教版 牛顿运动定律的综合应用 课时作业
一、选择题
1.(多选)下列关于超重、失重现象的描述,正确的是( )
A.列车在水平轨道上加速行驶,列车上的人处于超重状态
B.电梯正在减速下降,人在电梯中处于超重状态
C.蹦床运动员在空中上升阶段处于失重状态,下落阶段处于超重状态
D.神舟十一号飞船在竖直向上加速升空的过程中,飞船里的宇航员处于超重状态
解析:选BD 列车在水平轨道上加速行驶时,列车上的人在竖直方向上平衡,既不失重也不超重,A错误;电梯正在减速下降,加速度方向竖直向上,电梯里的人为超重状态,B正确;运动员在空中上升和下落阶段加速度都竖直向下,为失重状态,C错误;飞船加速升空的过程中,加速度向上,飞船中的宇航员处于超重状态,D正确.
2.物体A、B放在光滑的水平地面上,其质量之比mA∶mB=2∶1.现用水平3 N的拉力作用在物体A上,如图所示,则A对B的拉力等于( )
A.1 N B.1.5 N
C.2 N D.3 N
解析:选A 设B物体的质量为m,A对B的拉力为F,对A、B整体,根据牛顿第二定律得a=,对B有F=ma,所以F=1 N.
3. (多选)(2018届黄冈一模)如图所示,光滑水平地面上,可视为质点的两滑块A、B在水平外力的作用下紧靠在一起压缩弹簧,弹簧左端固定在墙壁上,此时弹簧的压缩量为x0,以两滑块此时的位置为坐标原点建立如图所示的一维坐标系,现将外力突然反向并使B向右做匀加速运动,下列关于外力F、两滑块间弹力FN与滑块B的位移x变化的关系图象可能正确的是( )
解析:选BD 设A、B向右匀加速运动的加速度大小为a,根据牛顿第二定律,对整体有F+k(x0-x)=(mA+mB)a,可得F=kx+(mA+mB)a-kx0,若(mA+mB)a=kx0,得F=kx,则F与x成正比,Fx图象可能是过原点的直线,对A有k(x0-x)-FN=mAa,得FN=-kx+kx0-mAa,可知FNx图象是向下倾斜的直线,当FN=0时A、B开始分离,此后B
做匀加速运动,F不变,则A、B开始分离时有x=x0-<x0,因此B和D是可能正确的.
4.如图所示,光滑水平面上放置着质量分别为m、2m的A、B两个物体,A、B间的最大静摩擦力为μmg,现用水平拉力F拉B,使A、B以同一加速度运动,则拉力F的最大值为( )
A.μmg B.2μmg
C.3μmg D.4μmg
解析:选C 当A、B之间恰好不发生相对滑动时力F最大,此时,对于A物体所受的合外力为μmg,由牛顿第二定律知aA==μg;对于A、B整体,加速度a=aA=μg,由牛顿第二定律得F=3ma=3μmg.
5. (多选)将一个质量为1 kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的vt图象如图所示,g取10 m/s2.下列说法中正确的是( )
A.小球所受重力和阻力之比为5∶1
B.小球上升过程与下落过程所用时间之比为2∶3
C.小球落回到抛出点时的速度大小为8 m/s
D.小球下落过程中,受到向上的空气阻力,处于超重状态
解析:选AC 上升过程中mg+Ff=ma1,由题图可知a1=12 m/s2,解得Ff=2 N,小球所受重力和阻力之比为5∶1,选项A正确;下落过程中mg-Ff=ma2,可得a2=8 m/s2,根据h=at2,可得==,选项B错误;根据v=a2t2,t2= s,可得v=8 m/s,选项C正确;小球下落过程中,加速度方向竖直向下,小球处于失重状态,选项D错误.
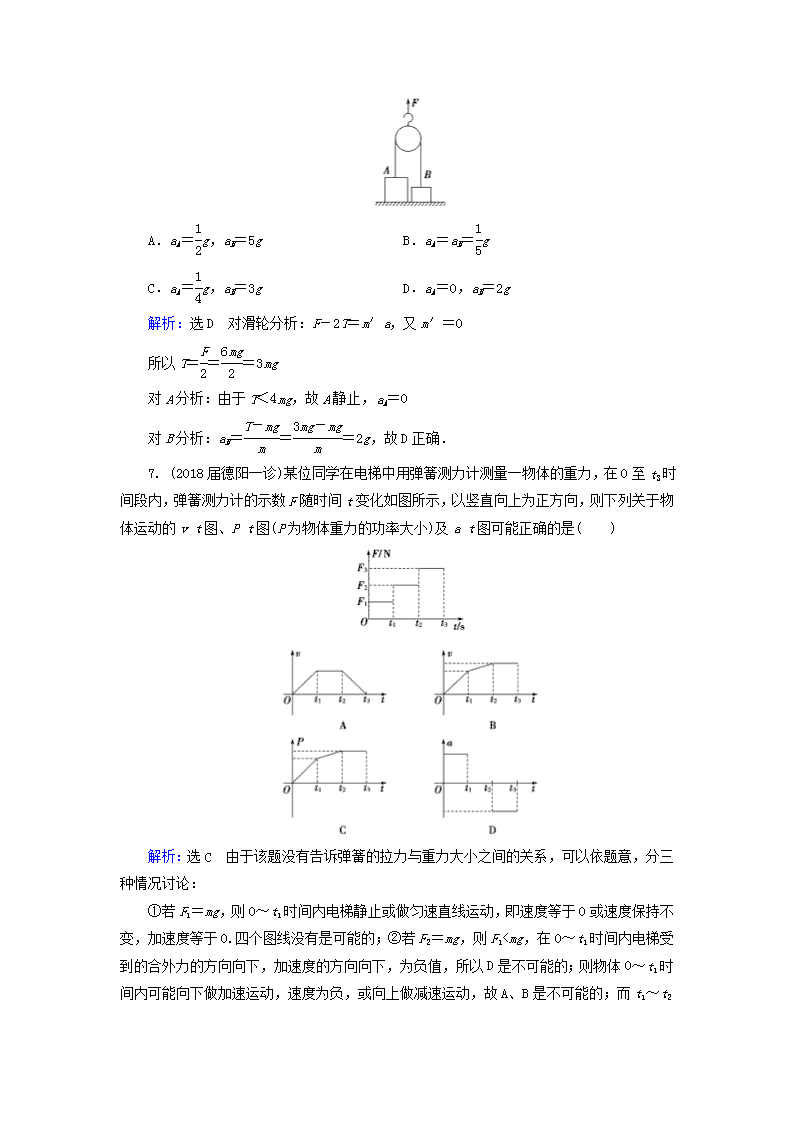
6. (2018届淮北一模)如图,物块A和B的质量分别为4m和m,开始A、B均静止,细绳拉直,在竖直向上拉力F=6mg作用下,动滑轮竖直向上加速运动.已知动滑轮质量忽略不计,动滑轮半径很小,不考虑绳与滑轮之间的摩擦,细绳足够长,在滑轮向上运动过程中,物块A和B的加速度分别为( )
A.aA=g,aB=5g B.aA=aB=g
C.aA=g,aB=3g D.aA=0,aB=2g
解析:选D 对滑轮分析:F-2T=m′a,又m′=0
所以T===3mg
对A分析:由于T<4mg,故A静止,aA=0
对B分析:aB===2g,故D正确.
7. (2018届德阳一诊)某位同学在电梯中用弹簧测力计测量一物体的重力,在0至t3时间段内,弹簧测力计的示数F随时间t变化如图所示,以竖直向上为正方向,则下列关于物体运动的vt图、Pt图(P为物体重力的功率大小)及at图可能正确的是( )
解析:选C 由于该题没有告诉弹簧的拉力与重力大小之间的关系,可以依题意,分三种情况讨论:
①若F1=mg,则0~t1时间内电梯静止或做匀速直线运动,即速度等于0或速度保持不变,加速度等于0.四个图线没有是可能的;②若F2=mg,则F1
mg,钢索最容易发生断裂,选项C、D错误.
3. (2018届甘肃一诊)如图所示,在水平面上,有两个质量分别为m1和m2的物体A、B,它们与水平面之间的动摩擦因数均为μ,m1>m2,A、B间水平连接着一轻质弹簧测力计.若用大小为F的水平力向右拉B,稳定后B的加速度大小为a1,弹簧测力计示数为F1;如果改用大小为F的水平力向左拉A,稳定后A的加速度大小为a2,弹簧测力计示数为F2.下列关系式正确的是( )
A.a1=a2,F1>F2 B.a1=a2,F1a2,F1>F2
解析:选A 以由A、B及弹簧组成的整体为研究对象,由牛顿第二定律得两次运动过程中整体的加速度a=,可得a1=a2=a.当用F拉B时,以A为研究对象有F1-μm1g=m1a1,可得F1=μm1g+m1a1=;同理,当用F拉A时,以B为研究对象,有F2-μm2g=m2a2,可得F2=,由于m1>m2,则F1>F2,A正确.
4.如图所示,质量均为m的A、B两物体叠放在竖直弹簧上并保持静止,用大小等于mg的恒力F向上拉B,运动距离为h时,B与A分离.下列说法正确的是( )
A.B和A刚分离时,弹簧长度等于原长
B.B和A刚分离时,它们的加速度为g
C.弹簧的劲度系数等于
D.在B与A分离之前,它们做匀加速直线运动
解析:选C A、B分离前,A、B共同做加速运动,由于F是恒力,而弹力是变力,故A、B做变加速直线运动,当两物体要分离时,FAB=0
对B:F-mg=ma
对A:kx-mg=ma
即F=kx时,A、B分离,此时弹簧仍处于压缩状态,
由F=mg,设用恒力F拉B前弹簧压缩量为x0,
则2mg=kx0,h=x0-x
解以上各式得k=,综上所述,只有C项正确.
5. (多选)(2019届哈尔滨三中模拟)如图所示,光滑水平面上放置着四个相同的木块,其中木块B与C之间用一轻弹簧相连,轻弹簧始终在弹性限度内.现用水平拉力F拉B木块,使四个木块以相同的加速度一起加速运动,则以下说法正确的是( )
A.一起加速过程中,C木块受到四个力的作用
B.一起加速过程中,D木块受到的静摩擦力大小为
C.一起加速过程中,A、D木块所受摩擦力大小和方向相同
D.当F撤去瞬间,A、D木块所受静摩擦力的大小和方向都不变
解析:选BC 在水平拉力F的作用下,四个木块以相同的加速度一起加速运动,则由牛顿第二定律可知,对整体有F=4ma,对A、D木块有fA=fD=ma,解得A、D木块所受摩擦力大小 fA=fD=,方向均水平向右,故B、C正确;一起加速过程中,C木块受到重力、D木块对其的压力和静摩擦力、地面对其的支持力及弹簧对其的弹力,共五个力的作用,故A项错误;当F撤去瞬间,D木块所受静摩擦力的大小和方向均不变,而A木块所受静摩擦力的大小不变但反向,故D项错误.
6.(多选)质量分别为M和m的物块形状大小均相同,将它们通过轻绳和光滑定滑轮连接,如图甲所示,沿斜面方向的绳子在各处均平行于倾角为α的斜面,M恰好能静止在斜面上,不考虑M、m与斜面之间的摩擦.若互换两物块位置,按图乙放置,然后释放M,斜面仍保持静止.则下列说法正确的是( )
A.轻绳的拉力等于Mg
B.轻绳的拉力等于mg
C.M运动的加速度大小为(1-sinα)g
D.M运动的加速度大小为g
解析:选BC 按题图甲放置时,M静止,则Mgsinα=mg,按题图乙放置时,由牛顿第二定律得Mg-mgsinα=(M+m)α,联立解得a=(1-sinα)g.对m由牛顿第二定律得T-mgsinα=ma,解得T=mg,故A、D错误,B、C正确.
7.(多选)图甲中,两滑块A和B叠放在光滑水平地面上,A的质量为m1,B的质量为m2.设A、B间的动摩擦因数为μ,作用在A上的水平拉力为F,最大静摩擦力等于滑动摩擦力.图乙为F与μ的关系图象,其直线方程为F=μ.下列说法正确的有( )
A.μ和F的值位于a区域时,A、B相对滑动
B.μ和F的值位于a区域时,A、B相对静止
C.μ和F的值位于b区域时,A、B相对滑动
D.μ和F的值位于b区域时,A、B相对静止
解析:选AD 当A、B间刚要发生相对滑动时静摩擦力达到最大值,以B为研究对象,由牛顿第二定律得μm1g=m2a,得a=.以整体为研究对象,由牛顿第二定律得F=(m1+m2)a=μ,可以知道,图中实线对应两个物体刚要发生相对滑动的情形.μ和F的值位于a区域时,该区域中的点与原点连线的斜率大于实线的斜率,即有>,可得F>μ,A、B相对滑动;μ和F的值位于b区域时,该区域中的点与原点连线的斜率小于实线的斜率,即有<,可得F<μ,A、B相对静止,故A、D项正确,B、C项错误.
8. (2018届黄冈质检)如图所示,bc为固定在小车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增加,M始终和小车保持相对静止,当加速度增加到2a时,( )
A.横杆对M的摩擦力增加到原来的2倍
B.横杆对M的弹力增加到原来的2倍
C.细线与竖直方向的夹角增加到原来的2倍
D.细线的拉力增加到原来的2倍
解析:选A 对小球和物块组成的整体,分析受力如图甲所示,根据牛顿第二定律得,水平方向:Ff=(M+m)a,竖直方向:FN=(M+m)g,则当加速度增加到2a时,横杆对M的摩擦力Ff增加到原来的2倍,横杆对M的弹力等于2个物体的总重力,保持不变,故A正确,B错误;以小球为研究对象,分析受力情况如图乙所示,由牛顿第二定律得mgtanθ=ma,解得tanθ=,当a增加到2倍时,tanθ变为2倍,但θ不是原来的2倍.细线的拉力FT=,可见,a变为2倍,FT不是原来的2倍,故C、D错误.
9.(多选)(2019届合肥模拟)如图甲所示,水平地面上固定一足够长的光滑斜面,斜面顶端有一理想定滑轮,一轻绳跨过滑轮,绳两端分别连接小物块A和B.保持A的质量不变,改变B的质量m,当B的质量连续改变时,得到A的加速度a随B的质量m变化的图线,如图乙所示.图中a1、a2、m0为未知量,设加速度沿斜面向上的方向为正方向,空气阻力不计,重力加速度g取9.8 m/s2,斜面的倾角为θ,下列说法正确的是( )
A.若θ已知,可求出A的质量
B.若θ未知,可求出乙图中a1的值
C.若θ已知,可求出乙图中a2的值
D.若θ已知,可求出乙图中m0的值
解析:选BC 根据牛顿第二定律得
对B得:mg-F=ma①
对A得:F-mAgsinθ=mAa②
联立得a=③
若θ已知,由③知,不能求出A的质量mA,故A错误;
由③式变形得a=
当m→∞时,a=a1=g,故B正确;
由③式得,m=0时,a=a2=-gsinθ,故C正确;
当a=0时,由③式得,m=m0=mAsinθ,可知m0不能求出,故D错误.
10.(多选)如图甲所示,水平面上有一倾角为θ的光滑斜面,斜面上用一平行于斜面的轻质细绳系一质量为m的小球.斜面以加速度a水平向右做匀加速直线运动,当系统稳定时,细绳对小球的拉力和斜面对小球的支持力分别为T和FN.若Ta图象如图乙所示,AB是直线,BC为曲线,重力加速度为g=10 m/s2.则( )
A.a= m/s2时,FN=0
B.小球质量m=0.1 kg
C.斜面倾角θ的正切值为
D.小球离开斜面之前,FN=0.8+0.06a(N)
解析:选ABC 小球离开斜面之前,以小球为研究对象,进行受力分析,可得Tcosθ-FNsinθ=ma,Tsinθ+FNcosθ=mg,联立解得FN=mgcosθ-masinθ,T=macosθ+mgsinθ,所以小球离开斜面之前,Ta图象呈线性关系,由题图乙可知a= m/s2时,FN=0,选项A正确;当a=0时,T=0.6 N,此时小球静止在斜面上,其受力如图1所示,所以mgsinθ=T;当a= m/s2时,斜面对小球的支持力恰好为零,其受力如图2所示,所以=ma,联立可得tanθ=,m=0.1 kg,选项B、C正确;将θ和m的值代入FN=mgcosθ-masinθ,得FN=0.8-0.06a(N),选项D错误.
二、非选择题
11.如图所示,倾角为45°的轨道AB和水平轨道BC在B处用一小段光滑圆弧轨道平滑连接,水平轨道上D点的正上方有一探测器,探测器只能探测处于其正下方的物体.一小物块自倾斜轨道AB上离水平轨道BC高h处由静止释放,以小物块运动到B处的时刻为计时零点,探测器只在t=2~5 s内工作.已知小物块与倾斜轨道AB和水平轨道BC间的动摩擦因数分别为μ1=0.5和μ2=0.1,BD段长为L=8 m,重力加速度g=10 m/s2,为使探测器在工作时间内能探测到小物块,求h的取值范围.
解析:设物块沿倾斜轨道AB运动的加速度为a1,由牛顿第二定律有mgsin45°-μ1mgcos45°=ma1
设物块到达B处的速度为vB,由速度—位移关系得
vB2=2a1·
物块在水平轨道BC上做减速运动的加速度大小为a2=μ2g
①设物块运动到D点时速度恰好为零,这种情况下vB最小,物块在水平轨道BC上运动的时间最长,则vB1==4 m/s,又t1==4 s
当物块在t1=4 s到达D点时.联立解得h1=1.6 m
②当物块在t2=2 s到达D点时L=vB2t2-a2t22
联立解得h2=2.5 m
为使探测器在工作时间内能探测到小物块,h的取值范围为
1.6 m≤h≤2.5 m.
答案:1.6 m≤h≤2.5 m
12.如图所示,一直立的轻质薄空心圆管长为L,在其上下端开口处各安放有一个质量分别为m和2m的圆柱形物块A、B,A、B紧贴管的内壁,厚度不计.A、B与管内壁间的最大静摩擦力分别是f1=mg、f2=2mg,且设滑动摩擦力与最大静摩擦力大小相等.管下方存在这样一个区域:当物块A进入该区域时受到一个竖直向上的恒力F作用,而B在该区域运动时不受它的作用,PQ、MN是该区域的上下水平边界,高度差为H(L>2H).现让管的下端从距上边界PQ高H处由静止释放,重力加速度为g.
(1)为使A、B间无相对运动,求F应满足的条件;
(2)若F=3mg,求物块A到达下边界MN时A、B间的距离.
解析:(1)设A、B与管不发生相对滑动时的共同加速度为a,A与管间的静摩擦力为fA.
对A、B整体有3mg-F=3ma
对A有mg+fA-F=ma,并且fA≤f1
联立解得F≤mg.
(2)A到达上边界PQ时的速度vA=
当F=3mg时,可知A相对于圆管向上滑动,设A的加速度为a1,则有mg+f1-F=ma1,解得a1=-g
A向下减速运动的位移为H时,速度刚好减小到零,此过程运动的时间t=
由于管的质量不计,在此过程中,A对管的摩擦力与B对管的摩擦力方向相反,大小均为mg,B受到管的摩擦
力小于2mg,则B与圆管相对静止,B和圆管整体受到重力和A对管的静摩擦力作用以vA为初速度、以a2为加速度做匀加速直线运动,根据牛顿第二定律可得
a2==
物块A到达下边界MN时A、B之间的距离为
ΔL=L-=L-H.
答案:(1)F≤mg (2)L-H